机器学习之KNN算法：基于pytorch在MNIST数据集上实现数据分类预测

1 KNN算法介绍

KNN算法又叫做K近邻算法，是众多机器学习算法里面最基础入门的算法。KNN算法是最简单的分类算法之一，同时，它也是最常用的分类算法之一。KNN算法是有监督学习中的分类算法，它看起来和Kmeans相似（Kmeans是无监督学习算法），但却是有本质区别的。

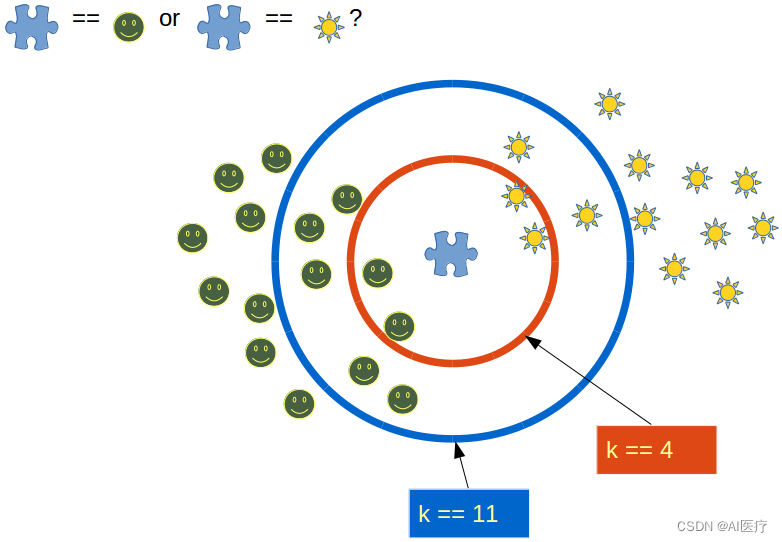
KNN算法基于实例之间的相似性进行分类或回归预测。在KNN算法中，要解决的问题是将新的数据点分配给已知类别中的某一类。该算法的核心思想是通过比较距离来确定最近邻的数据点，然后利用这些邻居的类别信息来决定待分类数据点的类别。其核心思想为：“近朱者赤近墨者黑”

1.1 KNN算法三要素

距离度量算法：一般使用的是欧氏距离。也可以使用其他距离：曼哈顿距离、切比雪夫距离、闵可夫斯基距离等。
k值的确定：k值越小，模型整体变得越复杂，越容易过拟合。通常使用交叉验证法来选取最优k值
分类决策：一般使用多数表决，即在 k 个临近的训练点钟的多数类决定输入实例的类。可以证明，多数表决规则等价于经验风险最小化

1.2 KNN是一种非参的，惰性的算法模型。

非参：并不是说这个算法不需要参数，而是意味着这个模型不会对数据做出任何的假设，与之相对的是线性回归总会假设线性回归是一条直线。KNN建立的模型结构是根据数据来决定的，这也比较符合现实的情况。
惰性：同样是分类算法，逻辑回归需要先对数据进行大量训练，最后会得到一个算法模型。而KNN算法却不需要，它没有明确的训练数据的过程，或者说这个过程很快。

1.3 KNN算法的优缺点

（1）KNN算法具有以下优点：

简单易懂：KNN算法的基本思想直观简单，易于理解和实现。
无需训练过程：KNN算法是一种基于实例的学习方法，不需要显式的训练过程。它直接利用已有的训练数据进行分类或回归预测。
适用于多类别问题：KNN算法可以应用于多类别问题，不受类别数目的限制。
对于不平衡数据集有效：KNN算法在处理不平衡数据集时相对较为有效，因为它不假设数据分布的先验知识。

（2）KNN算法的一些缺点：

计算复杂度高：在进行分类或回归预测时，KNN算法需要计算待分类数据点与所有训练数据点之间的距离。当训练数据集较大时，计算复杂度会显著增加。
对特征空间维度敏感：KNN算法对于特征空间的维度敏感。当特征空间维度较高时，由于所谓的"维度灾难"，KNN算法的性能可能会下降。在高维数据中，距离度量变得不准确，所有数据点都变得离得很远，失去了近邻的意义。
需要选择合适的K值：KNN算法的性能很大程度上取决于选择合适的最近邻数量K。选择过小的K值可能导致模型过于敏感，容易受到噪声的影响；选择过大的K值可能导致模型过于平滑，无法捕捉到细微的类别特征。
不适用于大规模数据集：由于KNN算法需要在预测阶段计算待分类数据点与所有训练数据点的距离，因此对于大规模数据集来说，存储和计算的开销可能会非常大。

KNN算法是一种简单但强大的分类和回归方法，适用于多种问题领域。但在使用时需要注意计算复杂度、维度敏感性、合适的K值选择以及适应大规模数据集的挑战。

2 KNN算法的应用场景

KNN算法的优点包括简单易懂、无需训练过程、适用于多类别问题等。KNN算法在许多领域中都有广泛的应用，KNN算法常见的应用场景如下：

分类问题：KNN算法可以用于分类问题，如文本分类、图像分类、语音识别等。通过比较待分类数据点与已知数据点之间的相似性，KNN可以将新的数据点分配到最相似的类别中。
回归问题：KNN算法也可以用于回归问题，如房价预测、股票价格预测等。通过计算最近邻数据点的平均值或加权平均值，KNN可以预测待分类数据点的数值属性。
推荐系统：KNN算法可以应用于推荐系统，根据用户之间的相似性来推荐相似兴趣的物品。通过比较用户之间的行为模式或兴趣偏好，KNN可以找到与当前用户最相似的一组用户，并向其推荐相似的物品。
异常检测：KNN算法可以用于检测异常数据点，如信用卡欺诈、网络入侵等。通过计算数据点与其最近邻之间的距离，KNN可以识别与大多数数据点不同的异常数据点。
文本挖掘：KNN算法可以用于文本挖掘任务，如文本分类、情感分析等。通过比较文本之间的相似性，KNN可以将新的文本数据点归类到相应的类别中。
图像处理：KNN算法可以应用于图像处理领域，如图像识别、图像检索等。通过比较图像之间的像素值或特征向量，KNN可以识别和检索相似的图像。

然而，该算法的缺点是计算复杂度高，特别是当训练数据集较大时，需要计算大量的距离。此外，KNN算法对于特征空间的维度敏感，对于高维数据的处理可能会出现问题。

针对部分数据（特征空间维度大，数据容量大）为了提高KNN算法的性能，可以使用特征选择和降维技术来减少特征空间的维度，以及采用KD树等数据结构来加速最近邻搜索过程。

KD Tree 是一种平衡二叉树，目的是实现对 k 维空间的划分。

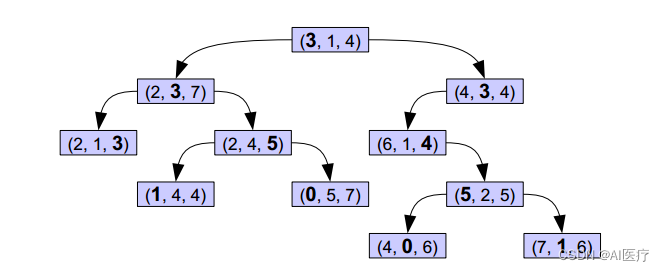
KDTree形似二叉搜索树，其实KDTree就是二叉搜索树的变种。这里的K = 3(维度).

KD树的组织原则

将每一个元组按0排序（第一项序号为0，第二项序号为1，第三项序号为2），在树的第n层，第 n%3 项被用粗体显示，而这些被粗体显示的树就是作为二叉搜索树的key值，比如，根节点的左子树中的每一个节点的第一个项均小于根节点的的第一项，右子树的节点中第一项均大于根节点的第一项，子树依次类推。

对于这样的一棵树，对其进行搜索节点会非常容易，给定一个元组，首先和根节点比较第一项，小于往左，大于往右，第二层比较第二项，依次类推。

KD树检索

假设我们的KDTree通过样本集{(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)}创建的。
我们来查找点(2.1,3.1)，在(7,2)点测试到达(5,4)，在(5,4)点测试到达(2,3)，然后search_path中的结点为<(7,2), (5,4), (2,3)>，从search_path中取出(2,3)作为当前最佳结点nearest, dist为0.141 （欧氏距离）；
然后回溯至(5,4)，以(2.1,3.1)为圆心，以dist=0.141为半径画一个圆，并不和超平面y=4相交，如下图，所以不必跳到结点(5,4)的右子空间去搜索，因为右子空间中不可能有更近样本点了。
于是在回溯至(7,2)，同理，以(2.1,3.1)为圆心，以dist=0.141为半径画一个圆并不和超平面x=7相交，所以也不用跳到结点(7,2)的右子空间去搜索。
至此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2.1,3.1)的最近邻点，最近距离为0.141。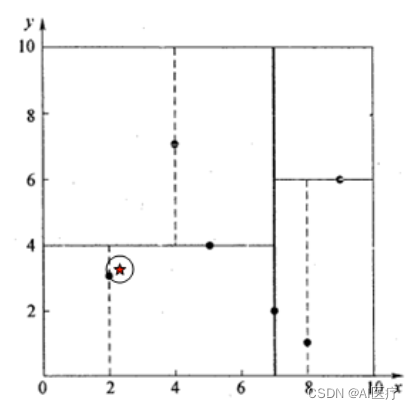

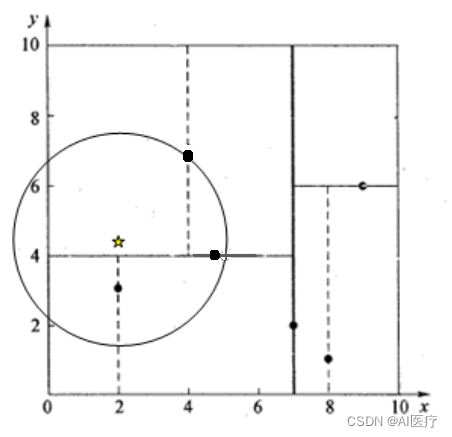
再举一个稍微复杂的例子，我们来查找点(2,4.5)，在(7,2)处测试到达(5,4)，在(5,4)处测试到达(4,7)，然后search_path中的结点为<(7,2), (5,4), (4,7)>，从search_path中取出(4,7)作为当前最佳结点nearest, dist为3.202；
然后回溯至(5,4)，以(2,4.5)为圆心，以dist=3.202为半径画一个圆与超平面y=4相交，如下图，所以需要跳到(5,4)的左子空间去搜索。所以要将(2,3)加入到search_path中，现在search_path中的结点为<(7,2), (2, 3)>；另外，(5,4)与(2,4.5)的距离为3.04 < dist = 3.202，所以将(5,4)赋给nearest，并且dist=3.04。
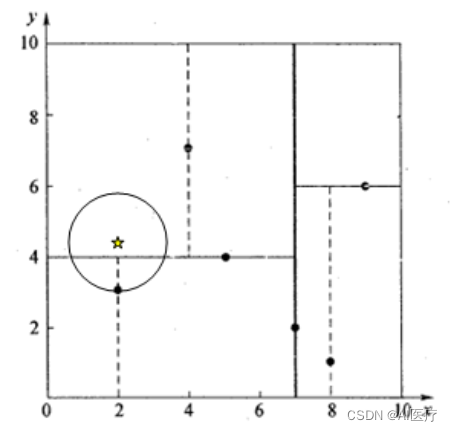
回溯至(2,3)，(2,3)是叶子节点，直接平判断(2,3)是否离(2,4.5)更近，计算得到距离为1.5，所以nearest更新为(2,3)，dist更新为(1.5)
回溯至(7,2)，同理，以(2,4.5)为圆心，以dist=1.5为半径画一个圆并不和超平面x=7相交, 所以不用跳到结点(7,2)的右子空间去搜索。
至此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2,4.5)的最近邻点，最近距离为1.5。

3 基于pytorch在MNIST数据集上实现数据分类

3.1 获取MNIST数据集

（1）代码自动下载

train_dataset = datasets.MNIST(root='data',  # 选择数据的根目录
                            train=True,  # 选择训练集
                            transform=None,  # 不使用任何数据预处理
                            download=True)  # 从网络上下载图片

test_dataset = datasets.MNIST(root='data',  # 选择数据的根目录
                           train=False,  # 选择测试集
                           transform=None,  # 不适用任何数据预处理
                           download=True)  # 从网络上下载图片

但这个自动下载可能会出错，错误如下：

urllib.error.ContentTooShortError: <urlopen error retrieval incomplete: got only 5303709 out of 9912422 bytes>

（2）手工下载数据集

下载地址：MNIST数据

下载完成后，放到data/MNIST/raw目录下

图片内容展示：

digit = train_loader.dataset.data[0] 
plt.imshow(digit, cmap=plt.cm.binary)
plt.show()
print(train_loader.dataset.targets[0])

3.2 KNN计算

以MNIST的60000张图片作为训练集，通过KNN计算对测试数据集的10000张图片全部打上标签。通过KNN算法比较测试图片与训练集中每一张图片，然后将它认为最相似的那个训练集图片的标签赋给这张测试图片
具体应该如何比较这两张图片呢？在本例中，比较图片就是比较28×28的像素块。最简单的方法就是逐个像素进行比较，最后将差异值全部加起来两张图片使用L1距离来进行比较。逐个像素求差值，然后将所有差值加起来得到一个数值。如果两张图片一模一样，那么L1距离为0，但是如果两张图片差别很大，那么，L1的值将会非常大。

def KNN_classify(k, dis_func, train_data, train_label, test_data):
    num_test = test_data.shape[0]  # 测试样本的数量
    label_list = []
    for idx in range(num_test):
        distances = dis_func(train_data, test_data[idx])
        nearest_k = np.argsort(distances)
        top_k = nearest_k[:k]  # 选取前k个距离
        class_count = {}
        for j in top_k:
            class_count[train_label[j]] = class_count.get(train_label[j], 0) + 1
        sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
        label_list.append(sorted_class_count[0][0])

    return np.array(label_list)

3.3 完整代码

#!/usr/bin/env python
# coding: utf-8


import operator
import matplotlib.pyplot as plt
import numpy as np
from torchvision import datasets, transforms
from torch.utils.data import DataLoader


batch_size = 100
train_dataset = datasets.MNIST(root='data',  # 选择数据的根目录
                            train=True,  # 选择训练集
                            transform=None,  # 不使用任何数据预处理
                            download=True)  # 从网络上下载图片

test_dataset = datasets.MNIST(root='data',  # 选择数据的根目录
                           train=False,  # 选择测试集
                           transform=None,  # 不适用任何数据预处理
                           download=True)  # 从网络上下载图片

train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=True)

print("train_data:", train_dataset.data.size())
print("train_labels:", train_dataset.data.size())
print("test_data:", test_dataset.data.size())
print("test_labels:", test_dataset.data.size())


# digit = train_loader.dataset.data[0]  # 取第一个图片的数据
# plt.imshow(digit, cmap=plt.cm.binary)
# plt.show()
# print(train_loader.dataset.targets[0])

# 欧式顿距离计算
def e_distance(dataset_a, data_b):
    return np.sqrt(np.sum(((dataset_a - np.tile(data_b, (dataset_a.shape[0], 1))) ** 2), axis=1))

# 曼哈顿距离计算
def m_distance(dataset_a, data_b):
    return np.sum(np.abs(train_data - np.tile(test_data[i], (train_data.shape[0], 1))), axis=1)


def KNN_classify(k, dis_func, train_data, train_label, test_data):
    num_test = test_data.shape[0]  # 测试样本的数量
    label_list = []
    for idx in range(num_test):
        distances = dis_func(train_data, test_data[idx])
        nearest_k = np.argsort(distances)
        top_k = nearest_k[:k]  # 选取前k个距离
        class_count = {}
        for j in top_k:
            class_count[train_label[j]] = class_count.get(train_label[j], 0) + 1
        sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
        label_list.append(sorted_class_count[0][0])

    return np.array(label_list)


def get_mean(data):
    data = np.reshape(data, (data.shape[0], -1))
    mean_image = np.mean(data, axis=0)
    return mean_image


def centralized(data, mean_image):
    data = data.reshape((data.shape[0], -1))
    data = data.astype(np.float64)
    data -= mean_image  # 减去图像均值，实现领均值化
    return data


if __name__ == '__main__':
    # 训练数据
    train_data = train_loader.dataset.data.numpy()
    train_data = train_data.reshape(train_data.shape[0], 28 * 28)
    
    # 归一化处理
    mean_image = get_mean(train_data)  # 计算所有图像均值
    train_data = centralized(train_data, mean_image)
    
    print('train_data shape:', train_data.shape)
    train_label = train_loader.dataset.targets.numpy()
    print('train_lable shape', train_label.shape)

    # 测试数据
    test_data = test_loader.dataset.data[:1000].numpy()
    test_data = centralized(test_data, mean_image)
    test_data = test_data.reshape(test_data.shape[0], 28 * 28)
    print('test_data shape', test_data.shape)
    test_label = test_loader.dataset.targets[:1000].numpy()
    print('test_label shape', test_label.shape)

    # 训练
    test_label_pred = KNN_classify(5, e_distance, train_data, train_label, test_data)

    # 得到训练准确率
    num_test = test_data.shape[0]
    num_correct = np.sum(test_label == test_label_pred)
    print(num_correct)
    accuracy = float(num_correct) / num_test
    print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))

3.4 计算结果展示

train_data: torch.Size([60000, 28, 28])
train_labels: torch.Size([60000, 28, 28])
test_data: torch.Size([10000, 28, 28])
test_labels: torch.Size([10000, 28, 28])
train_data shape: (60000, 784)
train_lable shape (60000,)
test_data shape (1000, 784)
test_label shape (1000,)
963
Got 963 / 1000 correct => accuracy: 0.963000

使用欧氏距离计算，最终结果准确率达到了96.3%

4 完整工程及数据下载

下载地址：代码和数据