【C++Coppeliasim】UR机械臂位置正逆解Coppeliasim集成测试

news2024/9/23 23:33:45

前言：

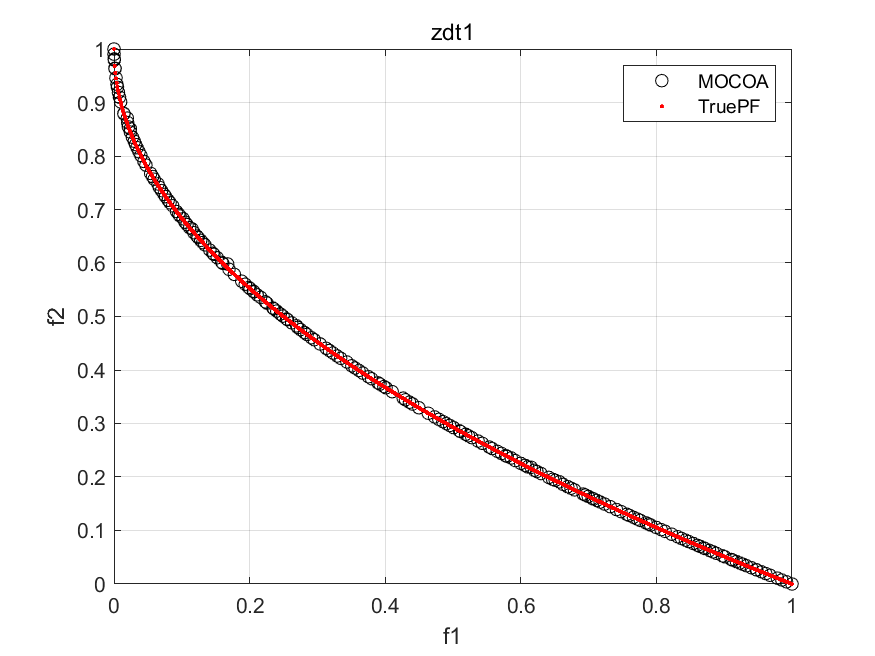
基于改进的 Denavit-Hartenberg 参数的UR机械臂正向运动学求解和基于几何分析的逆运动学求解。该代码在 C++ 和 MATLAB 中可用，两者都与 CoppeliaSim 集成。

该解决方案是使用 Microsoft Visual Studio 2022 和 C++ 20 标准构建的。

依赖：

Eigen

Eigen 是线性代数的 C++ 模板库：矩阵、向量、数值求解器和相关算法。

CoppeliaSim

使用他们的 C++ 远程 API：

在您的项目目录中包含以下文件：extApi.h、extApi.c、extApiPlatform.h 和 extApiPlatform.c；它们位于 CoppeliaSim 的安装目录中，在 programming/remoteApi 下；

将 NON_MATLAB_PARSING 和 MAX_EXT_API_CONNECTIONS=255（以及可选的 DO_NOT_USE_SHARED_MEMORY）定义为预处理器定义；

包括附加目录 remoteApi 和 include；

如果您对使用其调用的安全版本（如 fopen_s）不感兴趣，则需要在包含的头文件之前放置 _CRT_SECURE_NO_DEPRECATE 的定义。

思维导图：

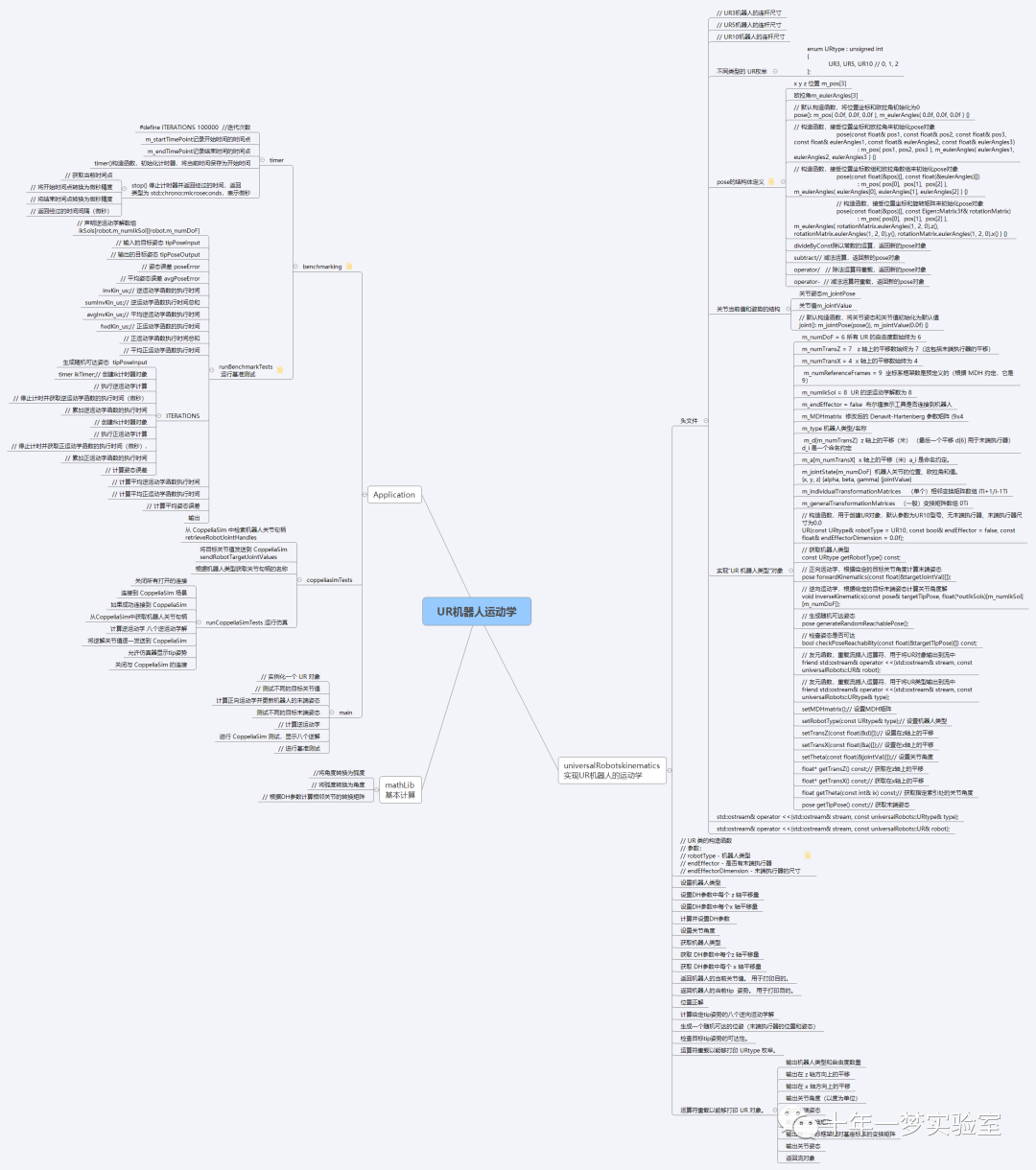
C++程序框架

视频演示

主程序：

#include <iostream>
#include "universalRobotsKinematics.h"
#include "coppeliaSimTests.h"
#include "benchmarking.h"




int main()
{
  //实例化一个 UR 对象
  universalRobots::UR robot(universalRobots::URtype::UR5);
  //universalRobots::UR robot(universalRobots::URtype::UR10);
  //测试不同的目标关节值
  const float targetJointValues[robot.m_numDoF] = { mathLib::rad(23), mathLib::rad(345), mathLib::rad(78), mathLib::rad(66), mathLib::rad(77), mathLib::rad(12) };
  // 计算正向运动学并更新机器人的末端姿态
  robot.forwardKinematics(targetJointValues);
  
  std::cout << robot << std::endl;
  //测试不同的目标末端姿态
  const universalRobots::pose targetTipPose = robot.forwardKinematics(targetJointValues);
  //计算逆运动学
  float ikSols[robot.m_numIkSol][robot.m_numDoF] = {};
  robot.inverseKinematics(targetTipPose, &ikSols);


  std::cout << "Inverse kinematics" << std::endl;
  for (unsigned int i = 0; i < robot.m_numIkSol; i++)
    std::cout << "IK solution " << i + 1 << ": " << mathLib::deg(ikSols[i][0]) << " " << mathLib::deg(ikSols[i][1]) << " " << mathLib::deg(ikSols[i][2]) << " " <<
    mathLib::deg(ikSols[i][3]) << " " << mathLib::deg(ikSols[i][4]) << " " << mathLib::deg(ikSols[i][5]) << std::endl;


   进行 CoppeliaSim 测试，显示八个逆解 
  coppeliaSim::runCoppeliaSimTests(robot, targetTipPose);


  //进行基准测试
  universalRobots::UR benchmarkRobot(universalRobots::URtype::UR5);
  benchmark::runBenchmarkTests(benchmarkRobot);


  std::cin.get();


  return 0;
}

笔记：

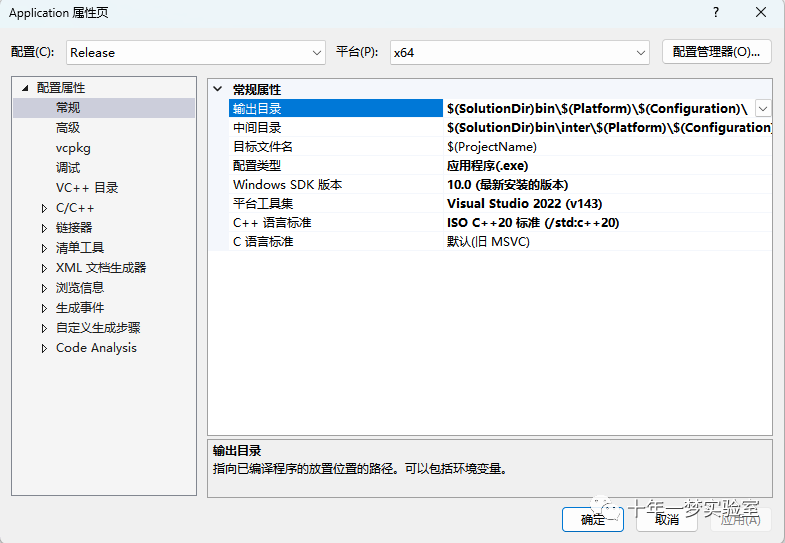
C++20

vcpkg

Eigen安装3.4

Eigen3.3会报错：“ { ”

Eigen::Matrix<float, m_numReferenceFrames, 4> m_MDHmatrix { {0.f, 0.f, m_d[0], m_jointState[0].m_jointValue},
            { mathLib::rad(-90),  0.f,      m_d[1],      m_jointState[1].m_jointValue + mathLib::rad(-90)},
            { 0.f,          m_a[0],    m_d[2],      m_jointState[2].m_jointValue },
            { 0.f,          m_a[1],    m_d[3],      m_jointState[3].m_jointValue },
            { 0.f,          m_a[2],    m_d[4],      mathLib::rad(90) },
            { mathLib::rad(90),  0.f,      0.f,        m_jointState[4].m_jointValue },
            { mathLib::rad(-90),  0.f,      0.f,        mathLib::rad(-90) },
            { 0.f,          m_a[3],    m_d[5],      m_jointState[5].m_jointValue },
            { 0.f,          0.f,      m_d[6],      0.f }
          };

pose结构的构造函数

struct pose
  {
    float m_pos[3] = {}; // x y z (meters)
    float m_eulerAngles[3] = {}; // alpha beta gamma (radians)
    // 默认构造函数，将位置坐标和欧拉角初始化为0
    pose()
      : m_pos{ 0.0f, 0.0f, 0.0f }, m_eulerAngles{ 0.0f, 0.0f, 0.0f } {}
    // 构造函数，接受位置坐标和欧拉角来初始化pose对象
    pose(const float& pos1, const float& pos2, const float& pos3, const float& eulerAngles1, const float& eulerAngles2, const float& eulerAngles3)
      : m_pos{ pos1, pos2, pos3 }, m_eulerAngles{ eulerAngles1, eulerAngles2, eulerAngles3 } {}
    // 构造函数，接受位置坐标数组和欧拉角数组来初始化pose对象
    pose(const float(&pos)[], const float(&eulerAngles)[])
      : m_pos{ pos[0],  pos[1],  pos[2] }, m_eulerAngles{ eulerAngles[0], eulerAngles[1], eulerAngles[2] } {}
    // 构造函数，接受位置坐标和旋转矩阵来初始化pose对象
    pose(const float(&pos)[], const Eigen::Matrix3f& rotationMatrix)
      : m_pos{ pos[0],  pos[1],  pos[2] }, m_eulerAngles{ rotationMatrix.eulerAngles(1, 2, 0).z(), rotationMatrix.eulerAngles(1, 2, 0).y(), rotationMatrix.eulerAngles(1, 2, 0).x() } {}
    
    // 除以常数的运算，返回新的pose对象
    pose divideByConst(const float& constant) const
{
      return pose(m_pos[0] / constant, m_pos[1] / constant, m_pos[2] / constant, m_eulerAngles[0] / constant, m_eulerAngles[1] / constant, m_eulerAngles[2] / constant);
    }
    // 减法运算，返回新的pose对象
    pose subtract(const pose& other) const
{
      return pose(m_pos[0] - other.m_pos[0], m_pos[1] - other.m_pos[1], m_pos[2] - other.m_pos[2], m_eulerAngles[0] - other.m_eulerAngles[0], m_eulerAngles[1] - other.m_eulerAngles[1], m_eulerAngles[2] - other.m_eulerAngles[2]);
    }
    // 除法运算符重载，返回新的pose对象
    pose operator/(const float& constant) const
    {
      return divideByConst(constant);
    }
    // 减法运算符重载，返回新的pose对象
    pose operator-(const pose& other) const
    {
      return subtract(other);
    }


  };

关节的构造函数：

struct joint
  {
    pose m_jointPose = {};// 关节姿态
    float m_jointValue = 0.0f;// 关节值
    // 默认构造函数，将关节姿态和关节值初始化为默认值
    joint()
      : m_jointPose(pose()), m_jointValue(0.0f) {}
  };

为什么要进行基准测试：（ChatGPT）