一、实验目的
1. 掌握图的基本存储方法;
2. 掌握有关图的操作算法并用高级语言实现;
3. 熟练掌握图的两种搜索路径的遍历方法。
二、实验内容
假设以一个带权有向图表示某一区域的公交线路网,图中顶点代表一些区域中的重要场所,弧代表已有的公交线路,弧上的权表示该线路上的票价(或搭乘所需时间),试设计一个交通指南系统,指导前来咨询者以最低的票价或最少的时间从区域中的某一场所到达另一场所。
三、实验步骤
1.用控制台输入和文件读入两种方式,把交通指南系统中的重要场所(定点)、公交线路(弧)、票价(弧上的权重)表示出来,存储在图中;
2.对图做初始化
3.深度优先DFS,标记已访问
4.贪心算法,更新最小票价
5.dijkstra算法,获取图中最短路径和最少票价
三、详细描述
(一) 数据结构设计
图论是数学的一个分支,图可以被表示为 G={V, E},其中 V={v1, ... , vN},E= {e1, ... , eM}。在本程序中,将顶点V用*vex描述,邻接矩阵用**arcs描述,顶点数和边数为vexNum,arcNum:
表 1 - 节点数据信息
| 数据项名称 | 数据项系统表示 | 数据类型 | 数据长度 | 备注 |
| 顶点 | vexs | char* | ||
| 邻接矩阵 | arcs | int** | ||
| 顶点数 | vexNum | int | ||
| 边数 | arcNum | int |
结构体函数如下:
(二)图的创建
1.图的初始化
定义Graph结构体,存放vexs(地点)、arcs(路径)、vexNum(地点数)、arcNum(路径数)。并编写initGraph函数,通过malloc函数动态分配空间。
初始化图,实质上就是给每个图中需要分配动态内存的地方都分配一个动态内存。
源码如下所示:
Graph* initGraph(int vexNum){
int i;
Graph* G = (Graph*)malloc(sizeof(Graph));//给图G分配一个动态空间
G->vexs = (char*)malloc(sizeof(char)*vexNum);//给顶点分配一个动态空间
G->arcs = (int**)malloc(sizeof(int*)*vexNum);//给邻接矩阵分配一个动态空间
for(i=0;i<vexNum;i++){
G->arcs[i] = (int*)malloc(sizeof(int)*vexNum);//循环给邻接矩阵的第二层分配动态空间
}
G->vexNum = vexNum;//传值传值传值-传顶点数
G->arcNum = 0;//给边数初始化为0
return G;//好的!这里全部分配完空间了,所以可以打包送走了
}2.图的创建
创建图,实质上就是把图中需要赋值的地方全部赋值一下,要注意的是,无向图的邻接矩阵是对称矩阵,源码如下:
void createGraph(Graph* G,char* vexs,int* arcs){
int i,j;
for(i=0;i<G->vexNum;i++){
G->vexs[i] = vexs[i];//先把顶点值传进去
for(j=0;j<G->vexNum;j++){
G->arcs[i][j] = *(arcs + i*G -> vexNum + j);//一维转二维了
if(G->arcs[i][j] !=0 && G->arcs[i][j] != MAX)//数数有多少边
G->arcNum ++;//边数++
}
}G->arcNum /= 2;//边数要除以2,因为矩阵有两半
}
3.图的释放
创建图的时候分配了一个内存空间,相应地,销毁图的时候就需要释放掉这些空间。
void freeGraph(Graph* G){
int i;
for (i = 0; i < G->vexNum; i++)
{
free(G->vexs[i]);
free(G->arcs[i]);
}
free(G->vexs);
free(G->arcs);
free(G);
}(三)文件读取和控制台读取
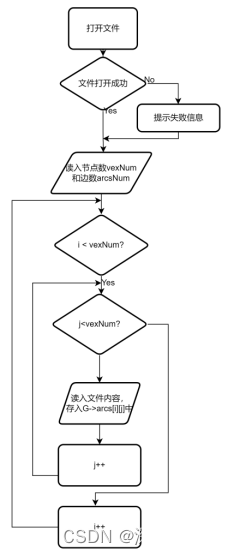
文件读取使用了FILE *file = fopen(filename, "r+");打开文件,然后依次对文件内容进行遍历读入,存入Graph G中,流程图如图 1所示。
控制台的读取也是直接将用户输入的内容存放到Graph G中。流程和文件读入类似,在这不过多赘述了。
(四)菜单设计
为了设计好看、便捷的菜单,这里调用了一个库conio.h,这个库里有个函数getch(),读入到用户输入后,不需要换行即可进行下一句。设计的原则是“直到用户输入正确为止”,流程图如图 2所示。

(五)迪杰斯特拉算法求最短路径和最少花费
迪杰斯特拉算法有三个关键元素,s记录了目标定点到其他顶点的最短路径是否求得,p记录了目标顶点到其他顶点的最短路径的前驱节点,d记录了目标顶点到其他顶点的最短路径的长度。首先对spd进行初始化,根据对应的顶点和路径赋初值。之后,首先通过getMin函数获取当前节点到其他所有节点中最短路径对应的节点,因为该路径已经是最短路径,如果在通过其他节点到达该路径那么一定会比当前路径长,所以获取到的最短路径就是对应的节点到初始节点的最短路径。之后根据将该最短路径作为中转,计算初始顶点和其他所有顶点的距离,在与我们初始化的距离作比较,如果相比较小,则记录在d数组中,之后再去获取最短路径,循环往复,直到获取完所有的最短路径。
测试阶段,使用excel工具模拟了一个邻接矩阵,如图 3所示。

使用画图工具,将上述邻接矩阵还原为图,如图 4所示。

图 4 图的画图模拟
迪杰斯特拉算法的流程图表达,如图 5所示。

图 5 迪杰斯特拉算法流程图
根据上述方法,求解出了最短路径,输出案例为:
The shortest path is:1-->6-->5
The shortest path spend is: 18
完整运行结果如下一节所示。
五、运行结果
(一)测试文件输入公交线路网的功能
*************欢迎来到交通指南系统*************
-------------------菜单列表-------------------
* 1.文件输入公交线路网 *
* 2.控制台输入公交线路网 *
* 0.退出程序 *
**********************************************
请选择:1
=====================
读入内容如下:
7 12
0 12 32767 32767 32767 16 14
12 0 10 32767 32767 7 32767
32767 10 0 3 5 6 32767
32767 32767 3 0 4 32767 32767
32767 32767 5 4 0 2 8
16 7 6 32767 2 0 9
14 32767 32767 32767 8 9 0
=====================
出发点:1
目的点:5
The shortest path is:1-->6-->5
The shortest path spend is: 18
-------按任意键回到主菜单--------
(二)测试控制台输入公交线路的功能
*************欢迎来到交通指南系统*************
-------------------菜单列表-------------------
* 1.文件输入公交线路网 *
* 2.控制台输入公交线路网 *
* 0.退出程序 *
**********************************************
请选择:2
请输入重要地点数:
4
============================================
1地到2地是否有直达线路?(有填1,没有填0):
1
请输入票价:
40
0-->1 票价:40
============================================
1地到3地是否有直达线路?(有填1,没有填0):
1
请输入票价:
30
0-->2 票价:30
============================================
1地到4地是否有直达线路?(有填1,没有填0):
0
read success
============================================
2地到3地是否有直达线路?(有填1,没有填0):
1
请输入票价:
90
1-->2 票价:90
============================================
2地到4地是否有直达线路?(有填1,没有填0):
1
请输入票价:
20
1-->3 票价:20
============================================
3地到4地是否有直达线路?(有填1,没有填0):
0
read success
=====================
读入内容如下:
4 4
0 40 30 32767
40 0 90 20
30 90 0 32767
32767 20 32767 0
=====================
出发点:1
目的点:3
The shortest path is:1-->3
The shortest path spend is: 30
-------按任意键回到主菜单--------
(三)测试输入错误及退出
*************欢迎来到交通指南系统*************
-------------------菜单列表-------------------
* 1.文件输入公交线路网 *
* 2.控制台输入公交线路网 *
* 0.退出程序 *
**********************************************
请选择:3
请选择:4
请选择:0
请按任意键继续. . .
六、心得与体会
这次的实验是图的最短路径的求解,共三种方法,弗洛伊德、迪杰斯特拉、Bellman-Ford算法。由于本程序是城市交通系统,不涉及权值为负的求解,因此,使用迪杰斯特拉算法就可以完成本题的求解。
实验一开始,肯定是要初始化、创建图,程序结束之后也得记得把申请的内存释放掉。相比以前,要用的时候就给这个地方申请内存的写法,我这次使用了统一在一个函数中申请内存,在一个函数中释放内存,比以前那种写法简直不要舒适太多。
本次实验的重点和难点是采用递归方式查询全部路径和采用迪杰斯特拉算法查询最短路径,递归方式查询全部路径的核心思想是递归查询当前节点的相邻节点,并将其确定为初始节点,递归判断初始节点与最终节点之间的路径。迪杰斯特拉算法查询最短路径的核心思想是每次获取当前节点相对其他所有节点的最短路径,在将其作为中继,生成新的路径,循环往复,最早找到当前节点相对于其他所有节点的最短路径。
在完成了代码的开发后,又开始了思考,能否对代码逻辑做一个优化,采用两种方式,一种是从文件读入,另一种是控制台输出,两种方法都做一个封装,提供给用户使用,带来更加舒适的使用体验。
这次的程序也存在缺点。比如释放图的那一步,我是最后才想起来做的,写程序的时候占了多少内存已经不知道了。还有就是对图的初始化,因为我得给每个点都放个名字,一开始设计结构体的时候没想起来,直接用了char*,然后一个一个裁了,导致地点名字只能是一个字符,如果当时用二维指针来做的话,这个问题就可以很好的解决了(可能在每个地点后面都补个,啥的也能解决)。其次,在设计createGraph这个函数的时候,把vexs直接传进去了,所以导致后面我如果想把接口提供给用户自己使用,又得写一个字符串的append函数,这些小瑕疵其实都可以在一开始设计结构体的时候就改为二维指针,直接规避掉。
最后,经过了此次实验,还是受益匪浅的,一个晚上一个奇迹,卡在ddl之前终于是结束了,舒了一口气,也可以开始课程设计的书写了。
七、源码
#include <stdio.h>
#include <stdlib.h>
#include <conio.h>
#define MAX 32767
typedef struct Graph{
char* vexs;//顶点
int** arcs;//邻接矩阵
int vexNum;//顶点数
int arcNum;//边数
}Graph;
//初始化一个图
//原理:全部分配动态空间
Graph* initGraph(int vexNum){
int i;
Graph* G = (Graph*)malloc(sizeof(Graph));//给图G分配一个动态空间
G->vexs = (char*)malloc(sizeof(char)*vexNum);//给顶点分配一个动态空间
G->arcs = (int**)malloc(sizeof(int*)*vexNum);//给邻接矩阵分配一个动态空间
for(i=0;i<vexNum;i++){
G->arcs[i] = (int*)malloc(sizeof(int)*vexNum);//循环给邻接矩阵的第二层分配动态空间
}
G->vexNum = vexNum;//传值传值传值-传顶点数
G->arcNum = 0;//给边数初始化为0
return G;//好的!这里全部分配完空间了,所以可以打包送走了
}
//释放内存
void freeGraph(Graph* G){
int i;
for (i = 0; i < G->vexNum; i++)
{
free(G->vexs[i]);
free(G->arcs[i]);
}
free(G->vexs);
free(G->arcs);
free(G);
}
//创建一个图
//原理:循环,把顶点值和邻接矩阵都传进去,顺便把边数数出来 ,当然,是用顶点数组和边数组来传
void createGraph(Graph* G,char* vexs,int* arcs){
int i,j;
for(i=0;i<G->vexNum;i++){
G->vexs[i] = vexs[i];//先把顶点值传进去
for(j=0;j<G->vexNum;j++){
G->arcs[i][j] = *(arcs + i*G -> vexNum + j);//一维转二维了
if(G->arcs[i][j] !=0 && G->arcs[i][j] != MAX)//数数有多少边
G->arcNum ++;//边数++
}
}
G->arcNum /= 2;//边数要除以2,因为矩阵有两半
}
//深度优先遍历
//原理:打印出这个点的值,标记为已访问,
void DFS(Graph* G,int* visited,int index){
int i;
visited[index] = 1;//打印过就标记
for(i=0;i<G->vexNum;i++){
if(G->arcs[index][i] > 0 && G->arcs[index][i] != MAX && !visited[i])//如果这个点和别的点有联系,并且没访问过,就遍历!
DFS(G,visited,i);
}
}
//获取最小值
//原理 :找到最小值,返回顶点序号
int getMin(Graph* G,int* d,int* s){
int i;
int min = MAX;//先把值初始化为最大值
int index;
for(i=0;i<G->vexNum;i++){
if(!s[i] && d[i]<min){
min = d[i];//最小值修改为最短路径
index = i;//最小的顶点序号给他丢进index里去
}
}
return index;
}
//迪杰斯特拉算法
//原理:
void dijkstra(Graph *G, int end,int index){
int i,j;
int *s = (int *)malloc(sizeof(int) * G->vexNum);
int *p = (int *)malloc(sizeof(int) * G->vexNum);
int *d = (int *)malloc(sizeof(int) * G->vexNum);
for (i = 0; i < G->vexNum; i++){
if (G->arcs[index][i] > 0 && G->arcs[index][i] != MAX){
s[i] = 0;
p[i] = index;
d[i] = G->arcs[index][i];
}
else if (G->arcs[index][i] == 0){
s[i] = 1;
p[i] = -1;
d[i] = 0;
}
else{
s[i] = 0;
p[i] = -1;
d[i] = MAX;
}
}
for (i = 0; i < G->vexNum - 1; i++){
int index = getMin(G, d, s);
s[index] = 1;
for (j = 0; j < G->vexNum; j++){
if (!s[j] && d[index] + G->arcs[index][j] < d[j]) {
d[j] = d[index] + G->arcs[index][j];
p[j] = index;
}
}
}
printf("The shortest path is:");
int current = end;
while(end != index){
printf("%c-->",G->vexs[end]);
end = p[end];
}
printf("%c\n",G->vexs[end]);
printf("The shortest path spend is: %d\n",d[current]);
free(s);
free(p);
free(d);
}
void read_file_to_arcs(char* filename,Graph *G){
int i,j;
FILE *file = fopen(filename, "r+");
if (file == NULL) {
file = fopen(filename, "w");
if (file == NULL) printf("\n\t文件创建失败!");
} else {
fscanf(file,"%d",&G->vexNum);
fscanf(file,"%d",&G->arcNum);
for(i=0;i<G->vexNum;i++){
for(j=0;j<G->vexNum;j++){
fscanf(file,"%d",&G->arcs[i][j]);
}
}
}
}
void read_scaner_to_arcs(Graph *G){
int i,j,has_road;
G->arcNum = 0;
printf("请输入重要地点数:\n");
scanf("%d",&G->vexNum);
for(i=0;i<G->vexNum-1;i++){
G->arcs[i][i] = 0;
for(j=i+1;j<G->vexNum;j++){
printf("============================================\n");
printf("%d地到%d地是否有直达线路?(有填1,没有填0):\n",i+1,j+1);
scanf("%d",&has_road);
if(has_road==1){
printf("请输入票价:\n");
scanf("%d",&G->arcs[i][j]);
G->arcs[j][i] = G->arcs[i][j];
printf("%d-->%d 票价:%d\n",i,j,G->arcs[i][j]);
G->arcNum++;
}else{
G->arcs[i][j] = MAX;
G->arcs[j][i] = G->arcs[i][j];
printf("read success\n");
}
}
}
G->arcs[i][i] = 0;
}
void printGraph(Graph *G){
int i,j;
printf("%d %d\n",G->vexNum,G->arcNum);
for(i=0;i<G->vexNum;i++){
for(j=0;j<G->vexNum;j++){
printf("%d ",G->arcs[i][j]);
}
printf("\n");
}
}
void menu(){
int i,start=0,end=0;
Graph* G = initGraph(7);
G->vexs = "1234567";
system("cls");
char ch;
printf("*************欢迎来到交通指南系统*************\n");
printf("-------------------菜单列表-------------------\n");
printf("* 1.文件输入公交线路网 *\n");
printf("* 2.控制台输入公交线路网 *\n");
printf("* 0.退出程序 *\n");
printf("**********************************************\n");
do{
printf("请选择:");
ch = getchar();
fflush(stdin);
int* visited = (int*)malloc(sizeof(int)*G->vexNum);
for(i=0;i<G->vexNum;i++){
visited[i] = 0;
}
switch(ch){
case '1':
read_file_to_arcs("4.txt",G);
printf("=====================\n");
printf("读入内容如下:\n");
printGraph(G);
printf("=====================\n");
printf("出发点:");
scanf("%d",&start);
printf("目的点:");
scanf("%d",&end);
DFS(G,visited,0);
printf("\n");
dijkstra(G,start-1,end-1);
printf("\n");
printf("\n-------按任意键回到主菜单--------");
getch();
getchar();
menu();
break;
case '2':
read_scaner_to_arcs(G);
printf("=====================\n");
printf("读入内容如下:\n");
printGraph(G);
printf("=====================\n");
printf("出发点:");
scanf("%d",&start);
printf("目的点:");
scanf("%d",&end);
DFS(G,visited,0);
printf("\n");
dijkstra(G,start-1,end-1);
printf("\n");
printf("\n-------按任意键回到主菜单--------");
getch();
getchar();
menu();
break;
case '0':
exit(0);
}
}while(ch!='0');
freeGraph(G);
}
int main(){
menu();
return 0;
}









![[论文笔记]Bidirectional LSTM-CRF Models for Sequence Tagging](https://img-blog.csdnimg.cn/img_convert/38075ffe980f55263caec6b4557dfc85.png)

