本专栏包含信息论与编码的核心知识,按知识点组织,可作为教学或学习的参考。markdown版本已归档至【Github仓库:https://github.com/timerring/information-theory 】或者公众号【AIShareLab】回复 信息论 获取。
文章目录
- 循环码的编码
- 循环码的伴随多项式译码
- 循环冗余校验 (Cyclic Redundancy Check, CRC)
循环码的编码
循环码编码用硬件实现时, 可用除法电路来实现。 除法电路主要是由移位寄存器和模 2 加法器组成。
r
(
x
)
=
x
n
−
k
u
(
x
)
m
o
d
g
(
x
)
c
(
x
)
=
x
n
−
k
u
(
x
)
+
r
(
x
)
\begin{array}{c} r(x)=x^{n-k} u(x) \bmod g(x) \\ c(x)=x^{n-k} u(x)+r(x) \end{array}
r(x)=xn−ku(x)modg(x)c(x)=xn−ku(x)+r(x)
码多项式中 x 的幂次代表移位的次数。
例如图给出 (7,3) 循环码编码器的组成。 g ( x ) = 1 + x + x 2 + x 4 g(x)=1+x+x^{2}+x^{4} g(x)=1+x+x2+x4。图中对应 g(x) 有4级移位寄存器, 分别用 D 1 , D 2 , D 3 , D 4 D_{1}, D_{2}, D_{3} , D_{4} D1,D2,D3,D4表示。
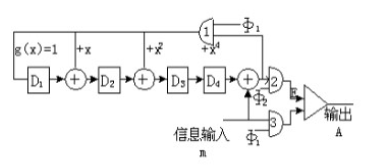
g(x) 多项式中系数是 1 或 0 表示该位上反馈线的有无, 信号 Φ 1 \Phi_{1} Φ1, Φ 2 \quad \Phi_{2} Φ2 , 控制门电路1-3。当信息位输入时, 控制信号使门1, 门3打开, 门2关闭, 输入信息码元一方面送 除法器进行运算, 另一方面直接输出。
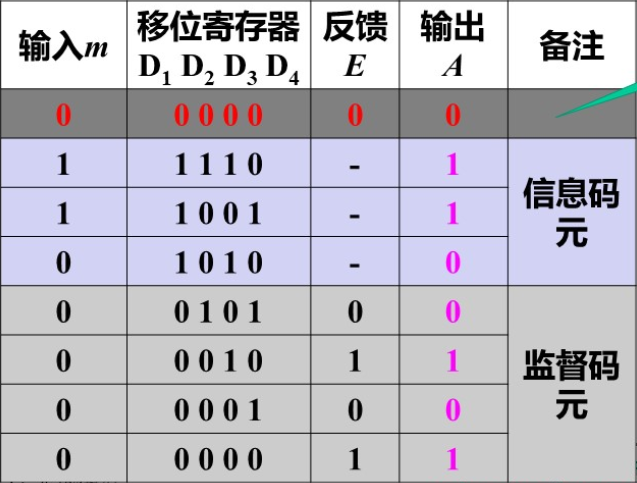
在信息位全部输入除法器之后, 控制信号使门1, 3关闭, 门2打开, 这 时寄存器通过门2直接输出, 将寄位寄存器中的除法余项依次取出, 即 将监督码元附加在信息码元之后。则编出的码组前面是原来 k \mathbf{k} k 个信息 码元,后面是(n-k)个监督码元,从而得到系统分组码。
为便于理解,下表给出这一编码器的工作过程。这里设信息码元为110,编出的监督码元为0101,循环码组为1100101。
循环码的伴随多项式译码
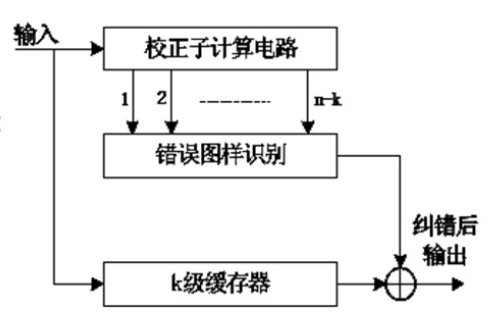
循环码的译码电路如图所示。
无错: y ( x ) m o d g ( x ) = 0 y(x)_{\bmod g(x)}=0 y(x)modg(x)=0 ;
有错: $y(x)_{\bmod g(x)} \neq 0 $ 。
收、发码字与错误图样多项式关系:
错误图样: e → = [ e 0 e 1 ⋯ e n − 1 ] ⇒ e ( x ) \overrightarrow{\boldsymbol{e}}=\left[e_{0} e_{1} \cdots e_{n-1}\right] \Rightarrow e(x) e=[e0e1⋯en−1]⇒e(x);
接收码字: y ( x ) = c ( x ) ⨁ e ( x ) \mathrm{y}(x)=c(x) \bigoplus e(x) y(x)=c(x)⨁e(x)
伴随式译码:
(1)对最可能出现的错误图样计算相应的伴随多项式: S ( x ) = e ( x ) m o d g ( x ) S(x)=e(x) \bmod g(x) S(x)=e(x)modg(x) , 并构造伴随式一错误图样表 [ ( S ⃗ , e ⃗ ) ] [(\vec{S}, \vec{e})] [(S,e)] ;
(2)根据接收码式计算伴随多项式; S ( x ) = y ( x ) m o d g ( x ) S(x)=y(x) \bmod g(x) S(x)=y(x)modg(x)
(3)由伴随式 S ⃗ \vec{S} S 查错误图样 e ⃗ \vec{e} e ;
(4)对接收码字进行纠错, 得到发送码字的估计值:
c
^
=
y
→
−
e
→
=
y
→
⊕
e
→
\hat{\mathbf{c}}=\overrightarrow{\mathbf{y}}-\overrightarrow{\mathbf{e}}=\overrightarrow{\mathbf{y}} \oplus \overrightarrow{\mathbf{e}}
c^=y−e=y⊕e
(5)循环码可以用移位寄存器实现伴随式译码
循环冗余校验 (Cyclic Redundancy Check, CRC)
适合于检测错误, 具有很强的检错能力, 且实现简单。
CRC检错性能如下:
- 可以检测出突发长度 < n − k + 1 <\boldsymbol{n}-\boldsymbol{k}+\boldsymbol{1} <n−k+1 的突发错误
- 大部分突发长度 = n − k + 1 =\boldsymbol{n}-\boldsymbol{k}+1 =n−k+1 的错误可以检测出, 其中不可检出的错误占 2 − ( n − k − 1 ) 2^{-(n-k-1)} 2−(n−k−1) ;
- 大部分突发长度 > n − k + 1 >\boldsymbol{n}-\boldsymbol{k}+\mathbf{1} >n−k+1 的错误可以检测出, 其中不可检出的错误占 2 − ( n − k ) 2^{-(n-k)} 2−(n−k) ;
- 可以检测出所有与许用码字码距 ≤ d min − 1 \leq d_{\min }-1 ≤dmin−1 的错误;
- 可以检测出所有奇数个错误。
- CRC不一定是循环码。但是码多项式一定是生成多 项式的倍式。
常用的CRC冗余校验码生成方程
CRC-16 g ( x ) = X 16 + X 15 + X 2 + 1 g(x)=X^{16}+X^{15}+X^{2}+1 g(x)=X16+X15+X2+1 (USB)
CRC-ITU g ( x ) = X 16 + X 12 + X 5 + 1 g(x)=X^{16}+X^{12}+X^{5}+1 g(x)=X16+X12+X5+1 (HDLC, PPP)
CRC-32
g
(
x
)
=
X
32
+
X
26
+
X
23
+
X
22
+
X
16
+
X
12
+
X
11
+
X
10
+
X
8
+
X
7
+
X
5
+
X
4
+
X
2
+
X
+
1
g(x)=X^{32}+X^{26}+X^{23}+X^{22}+X^{16}+X^{12}+ X^{11}+X^{10}+X^{8}+X^{7}+X^{5}+X^{4}+X^{2}+X+1
g(x)=X32+X26+X23+X22+X16+X12+X11+X10+X8+X7+X5+X4+X2+X+1 (LANS,
PPP)
注意:
- CRC不一定是循环码, 它是 (k+r, k) 线性分组码,其中 r 为 g(x) 的阶数;
- CRC码多项式一定是生成多项式的倍式;
- 生成多项式不一定是 x n + 1 x^{n}+1 xn+1 的因式;
- 编码过程和系统型循环码一样;
- 检错过程就是用接收码多项式除以生成多项式, 余式 ≠ 0 \neq \mathbf{0} =0 , 即为有错。
讨论:若已知CRC生成多项式 g(x) ,要信息位为 k \mathrm{k} k ,需 加入r位校验位,如何编码?
例: 若 g ( x ) = x 4 + x + 1 g(x)=x^{4}+x+1 g(x)=x4+x+1 ,已知数据信息为 110010110,现要对其进行CRC编码,如何编? 若收到的码字为 1100101001010 ,请问是否出错?
r=4 ; k \mathrm{k} k=9
码多项式的最高阶次为 12 .
x
4
u
(
x
)
=
x
12
+
x
11
+
x
8
+
x
6
+
x
5
r
(
x
)
=
x
4
u
(
x
)
m
o
d
g
(
x
)
=
x
3
+
x
2
+
x
\begin{array}{c} x^{4} u(x)=x^{12}+x^{11}+x^{8}+x^{6}+x^{5} \\ r(x)=x^{4} u(x) \bmod g(x)=x^{3}+x^{2}+x \end{array}
x4u(x)=x12+x11+x8+x6+x5r(x)=x4u(x)modg(x)=x3+x2+x
故编码为 1100101101110,码字1100101001010,有错,
r
(
x
)
=
x
≠
0
r(x)=x \neq 0
r(x)=x=0
参考文献:
- Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
- 周炯槃. 通信原理(第3版)[M]. 北京:北京邮电大学出版社, 2008.
- 樊昌信, 曹丽娜. 通信原理(第7版) [M]. 北京:国防工业出版社, 2012.