对之前的学习进行总结，整个比赛下来好像就用到了这个方法，最后也不知道对不对，反正最后还有点赶，就是很懵的那种，对于层次分析话的还是有点了解了，由于是纯小白，有错误的地方希望各位大佬能够指出。
目录
数据提取
归一化处理
判断矩阵
一致性检验
算术平均法求权重
加权求和
过程体会
数据提取
有些题目就会自己提供数据，数据是存储在Excel里面的，要导入的话我是用xlsread来实现的，因为是只用到了数值部分，所以另外两个参数就用~替代了。假设就是要提取“数学建模.xls”里面sheet1表中的内容，前面跟着的文件的绝对路径，用相对路径应该也可以吧，我这里没尝试了。
%[num, txt, raw] = xlsread(filename, sheet, range)
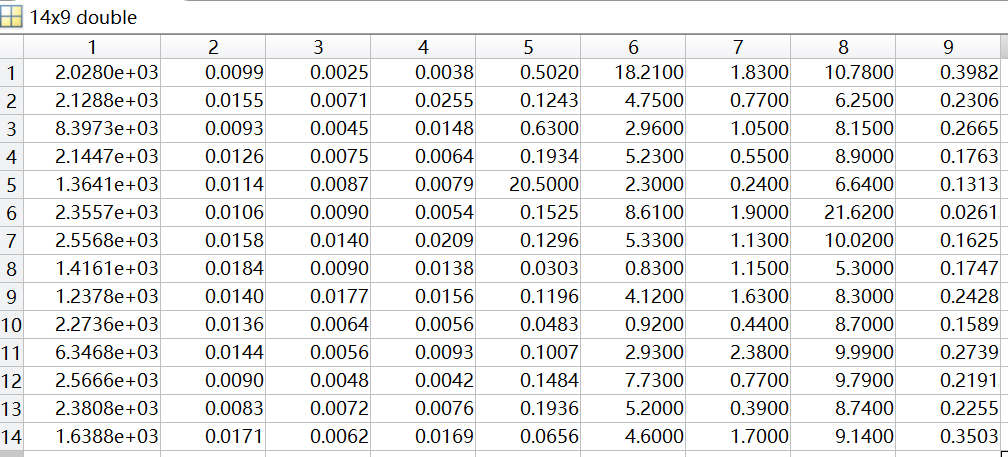
[num,~，~]=xlsread('C:\Users\25496\Desktop\数学建模.xls','sheet1');一般这种数据也是有规律的，集中在一块上面，直接就可以截取出来存在一个矩阵里面。如截取num中的1到10行，且5到14列的数据。如果有多组相同指标的数据，看是通过直接相加还是什么变成一组数据。
data=num(1:10,5:14);
这里有一个要注意的地方，因为不同指标之间的数量级不同，如果直接放在同一个矩阵里面，很小的数和一个更小的数放在一起，可能就会导致更小的整个指标的数据直接变成0，这显然是不被允许的，我当时的处理是把他们没个指标的数据放在集合中，因为后面要归一化处理，等处理之后在放在同一个矩阵里面，现在的话可以直接给他们整体乘以一个倍数，就可以让他们不至于被忽略了。
归一化处理
因为不同指标之间的数量级可以不用，指标内部的单位一致，但是指标和指标之后的值不同，这肯定是要进行归一化处理的，不然一个很大的数但是这个指标的权重却比较小，这不归一化处理这整个的误差就很大了。这里采用的是通过先求得整个指标数据的总和，再用每一个指标的数据除以整个总和，假设指标是一列一列的，就是用这一个数据除以这一列的总和得到一个数值。这样处理之后不同指标数量级一致，指标内部之间的排名没有发生改变。
这个计算的话，我比较担心的就是精度的问题了，然后可以直接通过循环来完成整个过程。这个除数的话习惯写还是用./，用/也行。
matlab中乘法“*”和点乘“.*”；除法“/”和点除“./”的联系和区别。_matlab 矩阵乘法_xiaotao_1的博客-CSDN博客
https://blog.csdn.net/xiaotao_1/article/details/79026406
%归一化处理
[mm,nn]=size(data);%数据行数和列数
for j=1:nn %针对每一列
msum=sum(data(:,j)); %求这一列元素之和
for i=1:mm
data(i,j)=data(i,j)./msum; %每一个元素的值都除以这行的和
end
end我当时是转换成元胞数组了，然后运算之后要变成矩阵的形式。
%归一化处理
[~,nn]=size(ingredient);
[mm,~]=size(ingredient{1});
for j=1:nn
msum=sum(ingredient1{j});
for i=1:mm
ingredient{j}(i)=ingredient{j}(i)./msum;
end
end
%元胞数组转矩阵
ing=cell2mat(ingredient);判断矩阵
因为不同指标之间的含义不同，所以侧重点也不同，所以一般是通过指标数值乘以权重再相加来区分重要性的，指标我们之前已经统一在同一个数量级了，现在我们要求的就是权重了。
首先就要人为设定一个判断矩阵，来表示指标之间的重要性，那么可以随便设定吗，这显然是不可以的，但是为什么不可以呢，因为我们对指标的重要性进行两两比较构造的判断矩阵，这可能就会导致出现不一致的情况，所以矩阵是否满足要求，就是要看他是否可以通过一致性检验。
一致性检验
计算一致性比例CR,CR=CI/RI，其中CI=(λmax-n)/(n-1),λmax为判断矩阵的最大特征值，n为指标数（判断矩阵行数），RI为平均随机一致性指标，通过查表可得到不同n对应的RI。
如果一致性比例CR=0，说明判断矩阵是一致矩阵，不会出现任何矛盾的情况。
如果一致性比例CR<0.1，可以认为判断矩阵一致举证的“差异”不大，通过一致性检验。
如果一致性比例CR>=0.1,需要修改判断矩阵，直到CR<0.1。
这个当时的话我一直不知道RI是什么意思，查表？到哪里查表，后面发现这个就是一个固定的东西。
RI=[0,0,0.58,0.9,1.12,1.24,1.32,1.41,1.45,1.49];然后对于判断矩阵的话，当时我们选了九个指标吧，可以想象当时的难度多大，不过还好通过一些特殊手段是直接得到了一个判断矩阵。缺点就是忽略的重要性那个东西，就是求出这个判断矩阵，通过判断矩阵来得到他们之间的重要性，调节指标在程序中的位置。
A=[1 3/2 3/4 1/5 1/4 3/2 2 3/4 1
2/3 1 1/2 1/4 1/6 1 3/2 1 1/2
4/3 2 1 1/3 1/2 2 3/2 1 3/2
5 4 3 1 2 4 5 2 4
4 6 2 1/2 1 3 4 2 5
2/3 1 1/2 1/4 1/3 1 3/2 1 1/2
1/2 2/3 2/3 1/5 1/4 2/3 1 1/3 2/3
4/3 1 1 1/2 1/2 2 3/2 1 3/2
1 2 2/3 1/4 1/5 2 3/2 2/3 1];那么怎么判断他对不对呢，就是要看一致性检验了。不得不说MATLAB是真的方便，最大特征值就求出来了。
A=[1 3/2 3/4 1/5 1/4 3/2 2 3/4 1
2/3 1 1/2 1/4 1/6 1 3/2 1 1/2
4/3 2 1 1/3 1/2 2 3/2 1 3/2
5 4 3 1 2 4 5 2 4
4 6 2 1/2 1 3 4 2 5
2/3 1 1/2 1/4 1/3 1 3/2 1 1/2
1/2 2/3 2/3 1/5 1/4 2/3 1 1/3 2/3
4/3 1 1 1/2 1/2 2 3/2 1 3/2
1 2 2/3 1/4 1/5 2 3/2 2/3 1];
%一致性检验
%求矩阵特征值
maxlam=max(eig(A));
[~,n]=size(A);
RI=[0,0,0.58,0.9,1.12,1.24,1.32,1.41,1.45,1.49];
CI=(maxlam-n)/(n-1);
CR=CI/RI(n);
if CR<0.10
disp("通过一致性检测")
else
disp("没有通过一致性检测")
return %终止运行
end
算术平均法求权重
这个我最终就是要求权重，那么每一个指标对应的权重怎么求呢？这里是通过算术平均法来求解的。
- 将通过一致性检验的判断矩阵按列归一化
- 每一列分别求和，求和的结果除以n，得到列向量就是权重向量。
%算数平均法求权重
[n,~]=size(A);
Asum=sum(A,1);%按列求和
Aprogress=A./(ones(n,1)*Asum);
%求权重向量
W=sum(Aprogress,2)./n;这里要注意的就是sum函数，sum(A,1)是按列求和，sum(Aprogress,2)是按行求和的。默认是按列求和的。
matlab中sum函数的用法_matlab sum函数_一只佳佳怪的博客-CSDN博客https://blog.csdn.net/iii66yy/article/details/128474643
加权求和
最后就是对所有的指标进行加权求和了，得到最后的总评分。
gred=ing*W;
当时我们是14个人，选了9个指标吧，也不知道是不是这样写的，最后就得到了这最后的一组数据，就是他们14个人的综合打分了，数值越大的就越优秀了。
过程体会
不太知道是否正确，就记录了整个的过程，下面是我自己对问题的理解：
为什么要对原始的指标进行归一化处理？
因为不同指标之间的数量级不同。
为什么要设定判断矩阵？
因为不同指标之间的侧重不同，假设指标A比指标B更加能够说明问题，那指标A肯定就比指标B更加重要一些。整个的设定过程本身就是主观的，好比一道菜肴，有人认为营养更加重要，也有人认为味道更加重要，所以这个设定就是看个人的倾向，能通过一致性检验的矩阵就是满足的矩阵。
为什么要用算术平均法求权重？
这个的话应该还有其他的方法，这里用的是算术平均分求的，先对判断矩阵进行归一化之后，就算术平均得到权重，当做整个指标的权重了。最后刚好行列向量相乘，得到最终的得分矩阵。
