✨博主：命运之光

🦄专栏：离散数学考前复习（知识点+题）

🍓专栏：概率论期末速成（一套卷）

🐳专栏：数字电路考前复习

🌟博主的其他文章：点击进入博主的主页

前言：身为大学生考前复习一定十分痛苦，你有没有过以下这些经历：

1.啊明天要考试了，关键这知识点它不进脑子啊。

2.小朋友，你是否有很多问号，为什么，快考试了你还啥也不会。

3.你们复习的时候，也是学着学着，手机就自动跳到手里了吗？

4.真正的大学生敢于直面崭新的课本。

5.睡也不敢睡，学也不想学。

6.监考老师+地理位置+附近战友友善度=考试分数。

🍓🍓当然以上都是开些玩笑，看看下面这些题，它可以让零基础未开始学习的你以最快的速度突击期末考试，毕竟把考题看会了，考试也就可以随随便便的通过了。

🌟填空题

🍓第五十九题

🍓第六十题

🍓第六十一题

🍓第六十二题

🍓第六十三题

🍓第六十四题

🍓第六十五题

🍓第六十六题

🍓第六十七题

🌟判断题

🍓第六十八题

🍓第六十九题

🍓第七十题

🍓第七十一题

🍓第七十二题

🍓第七十三题

🍓第七十四题

🍓第七十五题

🍓第七十六题

🍓第七十七题

🍓第七十八题

🍓第七十九题

🍓第八十题

🍓第八十一题

🍓第八十二题

🍓第八十三题

🍓第八十四题

🍓第八十五题

🍓第八十六题

🍓第八十七题

🍓第八十八题

🍓第八十九题

🍓第九十题

🍓第九十一题

🍓第九十二题

🍓第九十三题

🍓第九十四题

🍓第九十五题

🍓第九十六题

🍓第九十七题

🍓第九十八题

🍓第九十九题

🍓第一百题

🍓第一百零一题

🍓第一百零二题

🍓第一百零三题

🍓第一百零四题

🍓第一百零五题

🌸填空题和判断题就到此结束了，大家休息一下，我们接下来学习大题。

🍓结语

🌟填空题

🍓第五十九题

设U={a,b,c,d,e},A={c,d},A的特征函数的自变元e的函数值为____.

正确答案

🍓第六十题

整数集I上的<的自反闭包是____(用文字表达)。

正确答案

小于等于

🍓第六十一题

由3个命题变元p1,p2,p3组成的极大项M5为()

正确答案

p1∨￢p2∨p3

🍓第六十二题

偏序关系具有（）性，反对称性和传递性。

正确答案

自反

🍓第六十三题

拟序关系具有（）性，反对称性和传递性。

正确答案

反自反

🍓第六十四题

置换是（）射。

正确答案
双

🍓第六十五题

非多重图称为（）

正确答案

线图

🍓第六十六题

非多重图称为（）

正确答案

线图

🍓第六十七题

（）是自反的,反自反的,对称的,反对称的和可传递的。

正确答案

空集合上的空关系

🌟判断题

🍓第六十八题

当且仅当P→Q是一个重言式时,我们称“P蕴含Q”记作P=〉Q。

正确答案： √

🍓第六十九题

设A,B为两个命题公式A〈═〉B,当且仅当A↔B为一个重言式。

正确答案： √

🍓第七十题

个体,它是指可以独立存在的对象,它可以是一个具体事物,也可以是一个抽象的概念。

正确答案： √

🍓第七十一题

若关系R是自反的,当且仅当在关系矩阵中,主对角线上所有元素都是1;在关系图上每个结点都有自回路。

正确答案： √

🍓第七十二题

若关系R是对称的,当且仅当关系矩阵是对称的,在关系图上,任意两个结点间若有定向弧线,必是成对出现的。

正确答案： √

🍓第七十三题

没有一个关系既是对称的又是反对称的。

正确答案： ×

🍓第七十四题

一般来说指明个体性质或指明个体之间关系的是谓词。

正确答案： √

🍓第七十五题

个体变项的取值范围称为个体域,将一切事物组成的个体域称为全总个体域。

正确答案： √

🍓第七十六题

一般的,把与n个个体相关联的谓词叫做n元谓词。

正确答案： √

🍓第七十七题

通常把不带个体变项的谓词称为0元谓词。

正确答案： √

🍓第七十八题

在全称量词的描述中,特性谓词是条件式的前件,在存在量词中,特性谓词后跟一个合取项。

正确答案： √

🍓第七十九题

由一个或n个原子命题函数以及逻辑联结词组成的表达式称为复合命题函数。

正确答案： √

🍓第八十题

通常把命题、命题变元、谓词填式和命题函数叫做谓词演算的原子公式。

正确答案： √

🍓第八十一题

“好人自有好报”可用谓词公式表示如下:设F(x):x是好人;G(x):x会有好报,则命题符号化为:∀x(F(x)→G(x))。

正确答案： √

🍓第八十二题

“没有免费的午餐”可用谓词公式表示如下:设M(x):x是午餐;F(x): x是免费的,则命题符号化为:┐∃x(M(x)∧F(x))。也可以表示为:∀x(M(x)→┐F(x))。

正确答案： √

🍓第八十三题

在谓词公式中,紧接量词以后的最小子公式叫做该量词的辖域或作用域。

正确答案： √

🍓第八十四题

在一个谓词公式中,同一个变元既可以是约束的,又可以是自由的。

正确答案： √

🍓第八十五题

∀x P(x)∧∃yQ(x,y)整个谓词公式中只有一个量词。∀x的辖域为P(x),P(x)中的x和Q(x,y) 中的y是约束出现,Q(x,y)中的x是自由出现。

正确答案： ×

🍓第八十六题

对(∀x)(P(y)∧R(x,y))→(∃y)Q(y) 中的自由变元进行代入,则表示为: (∀x)(P(z)∧R(x,y))→(∃y)Q(y)。

正确答案： ×

🍓第八十七题

谓词公式如同命题公式,根据真值可分为永真式、矛盾式和可满足式。

正确答案： √

🍓第八十八题

设A、B是任意两个谓词公式,对A、B的任何赋值,若其真值相同,则称A与B是等价的,记作A ⇔B;若A→B是有效的,则称A蕴含B,记作A=>B。

正确答案： √

🍓第八十九题

谓词公式中,量词之前的否定联结词,不是否定该量词,而是否定该量词及其辖域。

正确答案： √

🍓第九十题

全集是相对的,不同的问题有不同的全集。即使是同一问题也可以取不同的全集。

正确答案： √

🍓第九十一题

一般地说,任意集合A至少有两个子集,一个是空集∅,另一个是它本身A。

正确答案： √

🍓第九十二题

设A为有限集合,则|ρ (A)|=2的|A|次方。

正确答案： √

🍓第九十三题

逻辑的方法表示序偶:(x,y)=(a,b)当且仅当(x=a)∧(y=b)。

正确答案： √

🍓第九十四题

如果A,B都是有限集,|A|= n,|B|= m,则|A×B|=nm=|A||B|。

正确答案： √

🍓第九十五题

设A,B,C,D是非空集合,则 A×B⊆C×D的充分必要条件是A⊆C且B⊆D。

正确答案： √

🍓第九十六题

若X×Y=X×Z,且X不是空集,则Y=Z。

正确答案： √

🍓第九十七题

设A={0,1},B={1,2},则A×B=B×A。

正确答案： ×

🍓第九十八题

集合的划分必然是其覆盖,但是覆盖不一定是划分。

正确答案： √

🍓第九十九题

设 A={a,b,c},则F={{a},{a,c}}是A 的一个覆盖。

正确答案： ×

🍓第一百题

设R是I上的关系,xRy当且仅当y=x+1,那么t(R)是关系<.' />

正确答案： √

🍓第一百零一题

{∧，∨}不是全功能联结词集合.

正确答案： √

🍓第一百零二题

P∨(Q∧R)的对偶为 P∧(Q∨R)。

正确答案： √

🍓第一百零三题

关系是序偶的集合,对它不能进行集合运算。

正确答案： ×

🍓第一百零四题

重言式中某个命题变元出现的某些地方代入以同一公式后，所得的仍是重言式。

正确答案： ×

🍓第一百零五题

正确答案： √

🌸填空题和判断题就到此结束了，大家休息一下，我们接下来学习大题。

🍓结语

❤️❤️一路看到这里，相信你的离散的考试应该已经增加了几分胜算💪🏻

❤️❤️如果喜欢本文请不吝点赞👍🏻，如果爱上本文请留下评论~

❤️❤️如果既不想点赞又不想评论…那么/(ㄒoㄒ)/~~还是祝愿你考试顺利啦~

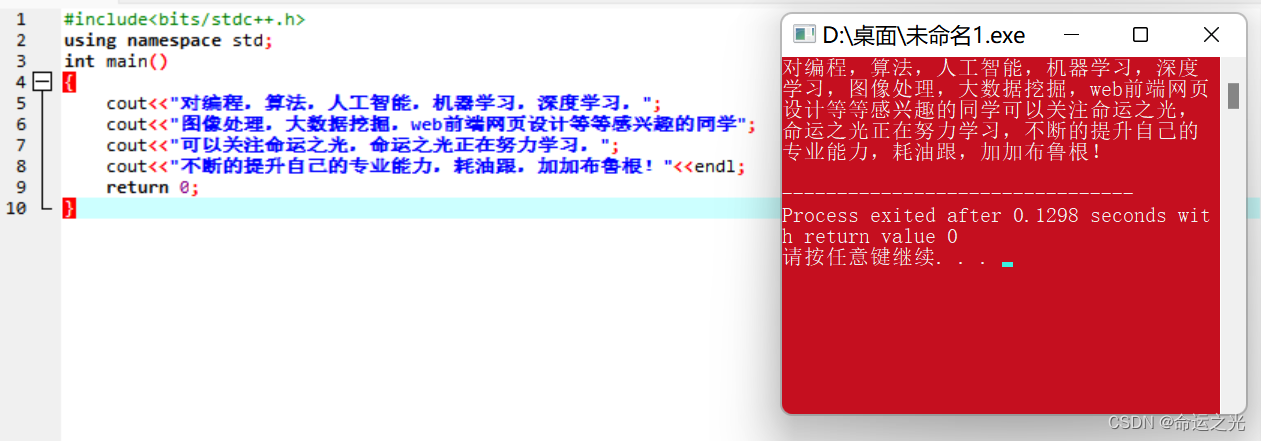
#include<bits/stdc++.h>
using namespace std;
int main()
{
    cout<<"对编程，算法，人工智能，机器学习，深度学习，";
    cout<<"图像处理，大数据挖掘，web前端网页设计等等感兴趣的同学";
    cout<<"可以关注命运之光，命运之光正在努力学习，";
    cout<<"不断的提升自己的专业能力，耗油跟，加加布鲁根！"<<endl; 
    return 0;
}