1.问题引入

通过前面深搜的学习，相信同学们已经掌握了搜索的基本思路。但有些问题直接搜索会得到部分分，并不会得到满分，而且分析其时间复杂度也很高。这时候就需要优化，提高搜索效率。

在之前的递归章节，已经介绍了一种优化方式——记忆化。本节重点学习剪枝的优化方式。

2.知识讲解

学习剪枝技巧之前，先来理解搜索中的一些术语，便于理解剪枝。

【搜索术语】

搜索树：从初始状态出发能访问的所有状态节点及对应路径构成的一棵树。

状态：各种属性，如位置、步数、总和、路径记录等等，有时通过参数记录，有时用全局变量记录。

回溯：是一种经常被用在深度优先搜索（DFS）的技巧。其基本思想是——从一条路往前走，能进则进，不能进则退回来，换一条路再试。典型的例题是：八皇后问题。

【剪枝】剪枝，顾名思义，就是通过一些判断，砍掉搜索树上不必要的子树。有时候，我们会发现某个结点对应的子树的状态都不是我们要的结果，那么我们其实没必要对这个分支进行搜索，砍掉这个子树，就是剪枝。

剪枝有很多种，下面介绍几种常用的剪枝：

（1）可行性剪枝：

在搜索过程中，一旦发现如果某些状态无论如何都不能找到最终的解，就可以将其“剪枝”了，比如越界操作、非法操作，也是用的最多的剪枝方法。一般通过条件判断来实现，如果新的状态节点是非法的，则不扩展该节点。例如：扫地机器人，不能超出边界的代码就属于可行性剪枝。

（2）预处理剪枝：

对于某些特殊的情况，可能不需要搜索或者搜索的数据量可以缩减，这时可以提前处理数据，便于加速后续搜索。一般在搜索之前预处理数据。

（3）重复性剪枝：

对于某一些特定的搜索方式，一个方案可能会被搜索很多次，这样是没必要的。在实现上，一般通过一个记忆数组来记录搜索到目前为止哪些状态已经被搜过了，然后在搜索过程中，如果新的状态已经被搜过了，则不再扩展该状态节点。例如：迷宫的第一条出路，就是把走过的路径标记掉，防止后面在错误的路径上反复搜索。

（4）最优性剪枝：

对于求最优解的一类问题，通常可以用最优性剪枝，比如在求解迷宫最短路的时候，如果发现当前的步数已经超过了当前最优解，那从当前状态开始的搜索都是多余的，因为这样搜索下去永远都搜不到更优的解。通过这样的剪枝，可以省去大量冗余的计算，避免超时。在实现上，一般通过状态变量或记忆数组来记录搜索到目前为止的最优解，然后在搜索过程中，如果新的状态已经不可能是最优解了，那再往下搜索肯定搜不到最优解，于是不再扩展该状态节点。

（5）顺序剪枝：

通常来讲，搜索的顺序可以不固定，算法可以进入搜索树的任意的一个子节点。但假如我们要搜索一个最小值，而非要从最大值存在的那个节点开搜，就可能存在搜索到最后才出解。而我们从最小的节点开搜很可能马上就出解。这就是顺序剪枝的一个应用。一般来讲，有单调性存在的搜索问题可以和贪心思想结合，进行顺序剪枝。例如：素数分解，可以发现分解方案从小到大具有单调性，采用贪心思想直接顺序搜索就可以得到答案。

通过上面概念的理解，会发现之前已经在很多例题中见到了不同剪枝的用法。下面再结合一些例题的思路和注释去理解剪枝的具体思路和做法。

3.例题解析

【例题1】工作分配问题。

设有n件工作分配给n个人(1≤n≤20)，将工作i分配给第j个人费用为Cij，为每个人分配一件不同的工作，对于给定的工作费用，计算最佳工作分配方案，使得总费用达到最小。第i行表示工作i分配给每个人需要的费用。

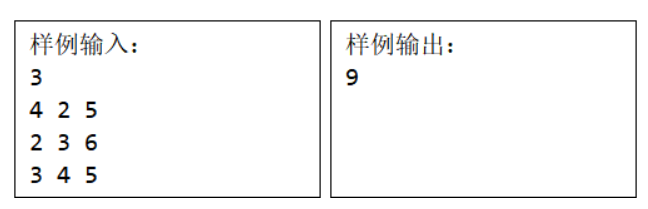
【问题分析】

此题问题类似于全排列问题，因为是n个不同的工作分配给不同的n个人，所以相当于n的全排列，但如果把所有的全排列列举一遍，肯定会超时。（不信的话，可以自己试一试之前的全排列问题需要多久才能运行出20的全排列）

优化方向：最优性剪枝。考虑到题目要求总费用最小，若当前的排列方案不符合之前求解的最小值，那么这种方案肯定不是最优的，提前剪枝。注意，不要在枚举完排列的时候判断最小，而是在过程中就可以判断了，也就是没选够n个工作就超过了之前最小的费用。

参考代码如下：

#include <bits/stdc++.h>
using namespace std;
int n;
int a[21][21];
int f[21];  //f[i]标记给第i人了安排了工作
int ans = INT_MAX;
//sum记录当前的和，cnt当前是第几个人，同时也表示当前的总人数
void dfs(int sum, int cnt) {
    if (cnt == n + 1) { //当递归到n+1时，前n个人都已选好
        ans = sum;
        return;
    }
    for (int i = 1; i <= n; i++) {
        if (f[i] == 0 && ans > sum + a[cnt][i]) {  //需要访问&&最优性剪枝
            f[i] = 1; //标记已访问
            dfs(sum + a[cnt][i], cnt + 1);
            f[i] = 0; //取消标记
        }
    }
}
int main() {
    cin >> n;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            cin >> a[i][j];
    dfs(0, 1);
    cout << ans;
}

【例题2】组合取数。

给出n个正整数x1,x2,...,xn，在这n个数中任取r个，请你计算r个数的和为质数的个数。（其中1≤r≤n≤30，每个正整数xi≤105）

解释：从5个数中任取3个的组合有10种。其中，只有8+12+9和13+7+9的和为质数29，所以答案为2种选法。

【问题分析】

这一题是选数类问题，标准的深搜代码。但阅读数据大小，会发现可能超时，超时的唯一原因就是搜索节点过多，那么如何优化呢？

优化方向一：采用可行性剪枝，减少无效搜索。在搜索的过程中，假如当前搜索到cur选择了cnt个数，那么还剩n-cur个数可以去选，还需要选择r-cnt个数。如果n-cur<r-cnt，那么就算后面所有的数都选择了，也无法达到目标状态。这样的情况我们就不需要去搜索了，可以剪枝。

优化方向二：采用预处理剪枝，提前减少搜索次数。本题是从n个数中选r个数，那么当r很大时，就容易因为递归过深导致超时；反向考虑一下，选r个数和不选n-r个数是等价的。如果r>n-r，那么选r个数就会比不选n-r个数的搜索深度要深。这时，我们去搜n-r个数来表示“不选”这些数，然后判断剩下的数的和是否是质数即可。

优化方向三：顺序剪枝。之前选过的数字不需要再次判断，可以用参数cur记录当前搜索的下标，之后每次选择的数字都是cur下标之后的数字。因此也不需要标记当前数字是否选择。

结合上述优化方向，参考代码如下：

#include <bits/stdc++.h>
using namespace std;
int n, x[35], r, ans, tot;  // tot:所有数字总和
bool flag;  // 是否反算，默认不反算
bool prime(int n) {
    if(n < 2) return 0;
  for(int i = 2; i <= n / i; i++)
    if(n % i == 0) return 0;
  return 1;
}
void dfs(int cur, int sum, int cnt) {  //参数：当前下标、当前总和、当前个数
    if (cnt == r) {
        if (flag && prime(tot - sum)) ans++;  //反向算，14行
        else if (!flag && prime(sum)) ans++;
        return;
    }
    if (cur > n) return;
    for (int i = cur + 1; i <= n - r + cnt + 1; i++)  //19行
        dfs(i, sum + x[i], cnt + 1);
}
int main() {
    cin >> n >> r;
    if (r > n - r) {  //若搜索数字个数超过一半，那么就采取搜索不取的个数
        flag = true;
        r = n - r;
    }
    for (int i = 1; i <= n; i++) {  //提前计算所有数字的总和tot
        cin >> x[i];
        tot += x[i];
    }
    dfs(0, 0, 0);
    cout << ans;
    return 0;
}

说明：

（1）解释一下14行代码的含义，flag为真说明需要反算，sum是反选的数字之和，tot-sum是正常选的数字之和，若正选的数字之和是质数，说明是一种取数的方案。

（2）第19行准备搜索选择下一个数时，也可以优化，若选取的数字不足，则不需要搜索了。即i 最大为 n-r+cnt+1。

请各位