✨博主:命运之光
🦄专栏:离散数学考前复习(知识点+题)
🍓专栏:概率论期末速成(一套卷)
🐳专栏:数字电路考前复习
✨博主的其他文章:点击进入博主的主页
前言: 身为大学生考前复习一定十分痛苦,你有没有过以下这些经历:
1.啊明天要考试了,关键这知识点它不进脑子啊。
2.小朋友,你是否有很多问号,为什么,快考试了你还啥也不会。
3.你们复习的时候,也是学着学着,手机就自动跳到手里了吗?
4.真正的大学生敢于直面崭新的课本。
5.睡也不敢睡,学也不想学。
6.监考老师+地理位置+附近战友友善度=考试分数。
🍓🍓当然以上都是开些玩笑,看看下面这些题,它可以让零基础未开始学习的你以最快的速度突击期末考试,毕竟把考题看会了,考试也就可以随随便便的通过了。

目录
🌟多选题
🍓第五十题
🍓第五十一题
🍓第五十二题
🍓第五十三题
🍓第五十四题
🍓第五十五题
🍓第五十六题
🍓第五十七题
🍓第五十八题
🌸多选题结束大家休息一下,即将进入填空题!
🍓结语
🌟多选题
🍓第五十题

🍓第五十一题

解析
B选项"x+y>0"并不是一个命题,因为它缺乏具体的上下文或数值,无法明确地判断为真或假。命题需要有明确的条件和值,才能进行判断。
选项D“我正在说谎”是一个悖论,无法确定其真实性,因此不是一个命题。
🍓第五十二题

🍓第五十三题

解析
A. {2} ∈ A:不正确。集合 A 中没有元素 {2}。
B. {2} ∈ B:正确。集合 B 中包含元素 {2},所以 {2} 是 B 的一个元素。
C. {2} ⊆ A:正确。因为集合 A 中存在元素 2,所以 {2} 是 A 的子集。
D. {2} ⊆ B:不正确。集合 B 中的元素 {2} 是另一个集合,而不是 B 的子集。
E. ∅ ∈ A:不正确。集合 A 中不存在空集。
F. ∅ ⊆ A:正确。空集是任何集合的子集,因此空集是 A 的子集。
🍓第五十四题

解析
A. ∅ ∈ A:正确。集合 A 中的唯一元素是空集 ∅,所以 ∅ 是 A 的一个元素。
B. ∅ ⊆ B:正确。空集 ∅ 是任何集合的子集,包括集合 B。
C. {∅} ∈ B:正确。集合 B 中的元素是幂集操作后的结果,其中包含子集 {∅}。
D. {{∅}} ∈ B:正确。集合 B 中的元素是幂集操作后的结果,其中包含子集 {{∅}}。
E. {{∅}} ⊆ B:正确。{{∅}} 是集合 B 的一个子集,因为 B 中包含幂集操作后的结果。
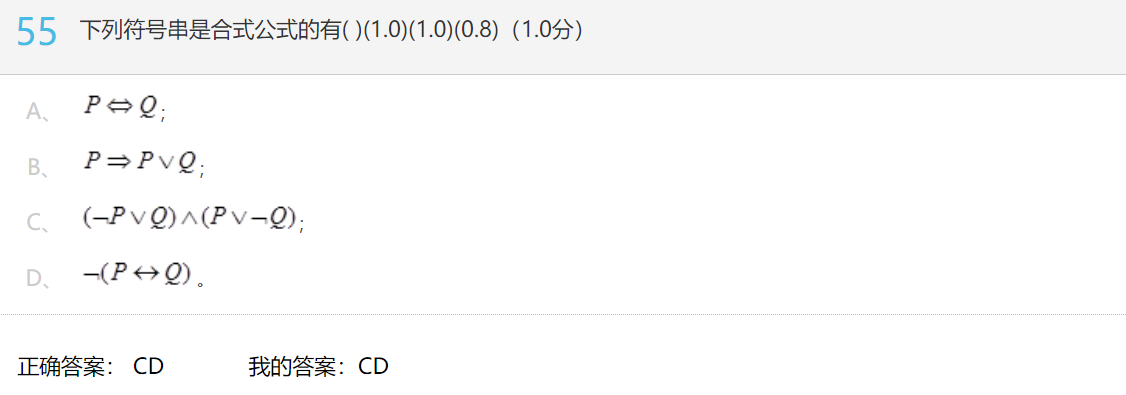
🍓第五十五题
解析
A、P⟺Q:这是一个非合式公式。⟺ 是逻辑中的双向蕴含符号,表示当且仅当 P 和 Q 的真值相等时为真。然而,合式公式必须符合语法和逻辑规则,但在这种情况下,P 和 Q 没有被定义或出现在其他公式中。
B 不是一个合式公式。在 B 中,P⟹P∨Q 的符号顺序不符合逻辑的语法规则,因此不是一个合法的公式。
C、(¬P∨Q)∧(P∨¬Q):这是一个合式公式。∧ 是逻辑中的合取符号,表示两个子公式都为真时为真。¬ 是逻辑中的非运算符号,表示取反。这个合式公式表示 P 和 Q 中至少有一个为真且至少有一个为假时为真。
D、¬(P⟺Q):这是一个合式公式。¬ 是逻辑中的非运算符号,表示取反。这个合式公式表示 P 和 Q 的真值不相等时为真。
🍓第五十六题

解析
A、x=13;:这是一个赋值语句,它并不陈述一个明确的真值,因此不是一个命题。
E、你打算考硕士研究生吗?:这是一个问句,它提出了一个问题,而不是一个陈述性陈述,因此不是一个命题。
🍓第五十七题

解析
A、{<0,0,1>,<0,0,2>,<0,1,1>,<0,1,2>,<1,0,1>,<1,1,1>,<1,1,2>}:这个选项表示一个由元组组成的集合,元组的元素来自集合A和B的笛卡尔积。但是,元组的长度为3,而集合A和B的元素个数不足以构建3个元素的元组。因此,这个选项不是一个表示集合的正确形式。
B、{<0,0,1>,<0,0,2>,<0,1,1>,<0,1,2>,<1,0,1>,<1,0,2>,<1,1,1>,<1,1,2>}:这个选项表示一个由元组组成的集合,元组的元素来自集合A和B的笛卡尔积。元组的长度为3,而集合A={0,1}和B={1,2}的元素个数足以构建3个元素的元组。因此,这个选项是一个表示集合的正确形式。
C、{<0,<0,1>>,<0,<0,2>>,<0,<1,1>>,<0,<1,2>>,<1,<0,1>>,<1,<0,2>>,<1,<1,1>>,<1,<1,2>>}:这个选项表示一个由元组组成的集合,其中元组的元素包括数字和元组。这不符合集合的定义,因为集合的元素应该是原子的、不可再分的。因此,这个选项不是一个表示集合的正确形式。
D、{<<0,0>,1>,<<0,0>,2>,<<0,1>,1>,<<0,1>,2>,<<1,0>,1>,<<1,0>,2>,<<1,1>,1>,<<1,1>,2>}:这个选项表示一个由元组组成的集合,其中元组的元素是元组和数字的组合。这不符合集合的定义,因为集合的元素应该是原子的、不可再分的。因此,这个选项不是一个表示集合的正确形式。
正确的答案是:选项 (B, D) 表示了一个集合。
🍓第五十八题

解析
根据给定的二元关系 R={<a,b>,<a,c>},我们可以逐个检查它是否具有所列出的性质。
A、自反性:对于所有的 a、b、c 属于 A,如果对于每个元素 x,都存在一个形如 <x,x> 的有序对,则关系 R 具有自反性。在给定的关系 R 中,不存在形如 <a,a>、<b,b>、<c,c> 的有序对,因此它不具有自反性。
B、反自反性:对于所有的 a、b、c 属于 A,如果对于每个元素 x,都不存在一个形如 <x,x> 的有序对,则关系 R 具有反自反性。在给定的关系 R 中,不存在形如 <a,a>、<b,b>、<c,c> 的有序对,因此它具有反自反性。
C、对称性:对于所有的 a、b 属于 A,如果对于每个形如 <a,b> 的有序对,则也存在一个形如 <b,a> 的有序对,则关系 R 具有对称性。在给定的关系 R 中,存在 <a,b> 的有序对,但不存在相应的 <b,a> 的有序对,因此它不具有对称性。
D、反对称性:对于所有的 a、b 属于 A,如果对于每个形如 <a,b> 和 <b,a> 的有序对,只有当 a=b 时才同时存在,则关系 R 具有反对称性。在给定的关系 R 中,存在 <a,b> 和 <a,c> 的有序对,但它们不满足 a=b 的条件,因此它具有反对称性。
E、传递性:对于所有的 a、b、c 属于 A,如果对于每个形如 <a,b> 和 <b,c> 的有序对,存在一个形如 <a,c> 的有序对,则关系 R 具有传递性。在给定的关系 R 中,存在 <a,b> 和 <b,c> 的有序对,且存在形如 <a,c> 的有序对,因此它具有传递性。
根据上述分析,关系 R 具有性质 B、D 和 E。
正确的答案是:选项 (B, D, E)。
🌸多选题结束大家休息一下,即将进入填空题!
🍓结语
❤️❤️一路看到这里,相信你的离散的考试应该已经增加了几分胜算💪🏻
❤️❤️如果喜欢本文请不吝点赞👍🏻,如果爱上本文请留下评论~
❤️❤️如果既不想点赞又不想评论…那么/(ㄒoㄒ)/~~还是祝愿你考试顺利啦~
#include<bits/stdc++.h>
using namespace std;
int main()
{
cout<<"对编程,算法,人工智能,机器学习,深度学习,";
cout<<"图像处理,大数据挖掘,web前端网页设计等等感兴趣的同学";
cout<<"可以关注命运之光,命运之光正在努力学习,";
cout<<"不断的提升自己的专业能力,耗油跟,加加布鲁根!"<<endl;
return 0;
}再接再厉,继续加油!