1. 概念

分治算法（divide and conquer）的核心思想其实就是四个字，分而治之 ，也就是将原问题划分成n个规模较小，并且结构与原问题相似的子问题，递归地解决这些子问题，然后再合并其结果，就得到原问题的解。

1.1 分治和递归的区别

分治算法是一种处理问题的思想，递归是一种编程技巧
分治算法的递归实现中，每一层递归都会涉及这样三个操作：

分解：将原问题分解成一系列子问题
解决：递归地求解各个子问题，若子问题足够小，则直接求解
合并：将子问题的结果合并成原问题

比如：
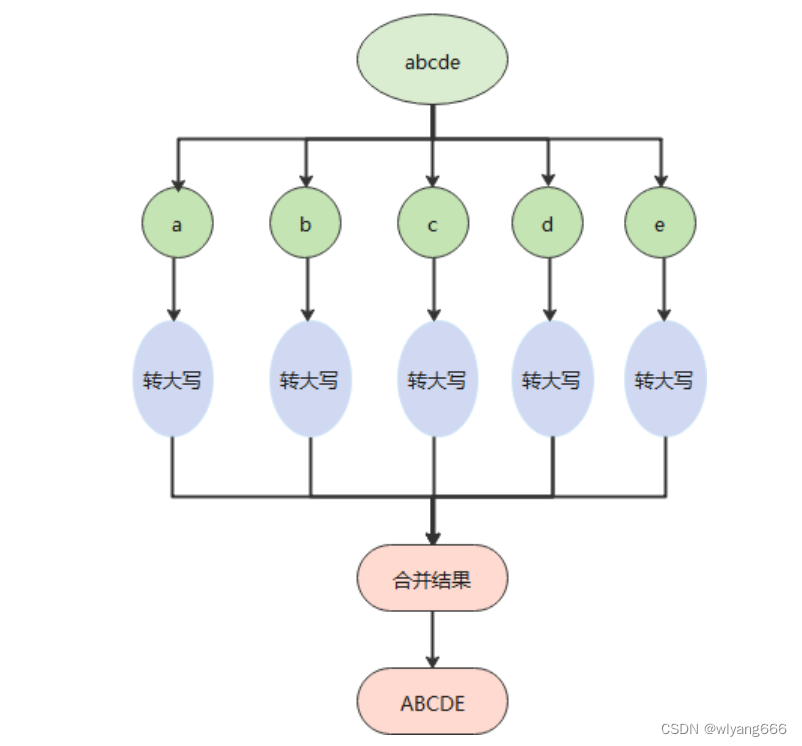
将字符串中的小写字母转化为大写字母
“abcde”转化为"ABCDE"
我们可以利用分治的思想将整个字符串转化成一个一个的字符处理

2. 经典问题

求X”问题
比如: 2的10次幂
一般的解法是循环10次

/**
 * @Description: 普通解法
 * @Author: wanlong
 * @Date: 2023/6/16 15:47
 * @param x:
 * @param n:
 * @return int
 **/
public static int commpow(int x, int n) {
    int s = 1;
    while (n >= 1) {
        s *= x;
        n--;
    }
    return s;
}

该方法的时间复杂度是：O(n)
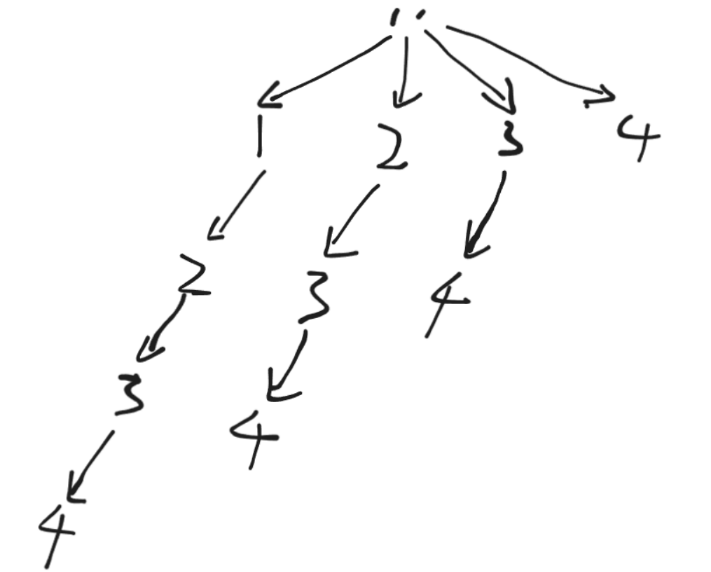
采用分治法
2^10拆成

/**
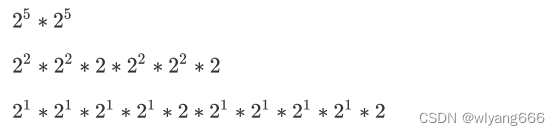
* @Description:分治解法
* @Author: wanlong
* @Date: 2023/6/16 15:47
* @param x:
* @param n:
* @return int
**/
public static int dividpow(int x, int n) {
   //递归结束 任何数的1次方都是它本身
   if (n == 1) {
       return x;
   }
   //每次分拆成幂的一半
   int half = dividpow(x, n / 2);
   //偶数
   if (n % 2 == 0) {
       return half * half;
   } else {
       return half * half * x;
   }
}

3. 时间复杂度

根据拆分情况可以是O(n)或O(logn)

4. 优缺点

优势：将复杂的问题拆分成简单的子问题，解决更容易，另外根据拆分规则，性能有可能提高。
劣势：子问题必须要一样，用相同的方式解决

5. 适用场景

分治算法能解决的问题，一般需要满足下面这几个条件：

1. 原问题与分解成的小问题具有相同的模式；
2. 原问题分解成的子问题可以独立求解，子问题之间没有相关性，这一点是分治算法跟动态规划的明显区别
3. 具有分解终止条件，也就是说，当问题足够小时，可以直接求解；
4. 可以将子问题合并成原问题，而这个合并操作的复杂度不能太高，否则就起不到减小算法总体复杂度的效果了。