1.题目
题目描述
Euler proved in one of his classic theorems that prime numbers are infinite in number.
But can every number be expressed as a summation of four positive primes? I don’t know
the answer. May be you can help!!! I want your solution to be very efficient as I have a
386 machine at home. But the time limit specified above is for a Pentium III 800
machine. The definition of prime number for this problem is “A prime number is a
positive number which has exactly two distinct integer factors”. As for example 37 is
prime as it has exactly two distinct integer factors 37 and 1.
输入
The input contains one integer number N (N<=10000000) in every line. This is the
number you will have to express as a summation of four primes. Input is terminated by
end of file.
输出
For each line of input there is one line of output, which contains four prime numbers
according to the given condition. If the number cannot be expressed as a summation of
four prime numbers print the line “Impossible.” in a single line. There can be multiple
solutions. Any good solution will be accepted.
样例输入
24
36
46样例输出
2 2 3 17
2 2 3 29
2 2 5 372.中文翻译
题目描述
欧拉在他的一个经典定理中证明了素数在数量上是无限的。但是,每个数字都可以表示为四个正素数的总和吗?我不知道答案。希望你能帮忙!!!我希望你的解决方案非常有效,因为我有386机器在家。但上面规定的时间限制是针对奔腾III 800 机器。这个问题的素数的定义是“素数是正的整数,正好有两个不同的整数因子”。例如,37是素数,因为它正好有两个不同的整数因子37和1。
输入
输入在每行中包含一个整数N(N<=100000)。这是你必须把这个数字表示为四个素数的总和。输入由终止文件末尾。
输出
每一行输入都有一行输出,根据给定的条件,其中包含四个素数。如果数字不能表示为四个素数在一行中打印出“ Impossible.”一行。可以有多个解决方案。任何好的解决方案都会被接受。
样例输入
24
36
46样例输出
2 2 3 17
2 2 3 29
2 2 5 373.思路代码(打印n以内所有情况的代码)(看注释即可)
下面的程序是打印n以内的所有可能情况
#encoding=utf-8
#利用欧拉筛 快速筛选包含n的n以内的所有素数
def euler_sieve(n):
primes=[]
status = [False] * 2 + [True] * (n - 1)
for i in range(2,n+1):
if status[i]:
primes.append(i)
for pj in primes:
if pj * i >n:
break
status[pj*i]= False
if i % pj == 0:
break
return primes
#主程序
while True:
#n表示输入的数
n=int(input())
#kk用来接收欧拉筛出的素数表
kk=euler_sieve(n)
#asn用来存储所有可能的结果
asn=[]
#found=1表示找到了解
found=0
#遍历素数表 下面的遍历思想和m=sqrt(n)的思想是一致的
for p1 in kk:
if p1 > n//4 +1:
break
for p2 in kk:
if p2 >(n-p2)//3 +1:
break
for p3 in kk:
if p3>(n-p1-p2)//2 +1:
break
p4=n-p1-p2-p3
if p4 in kk:
asn.append([p1,p2,p3,p4])
found=True
#如果找到
if found :
#下面首先要进行去重操作 :就是[2,2,3,17] 和[2,3,17,2] 其实是一种情况
#去重操作利用的是set集合元素不可重复的性质
sortedlist=[]
#先将asn list 中的所有列表元素排序 然后转化为元组,因为list不可hash
for i in asn:
sortedlist.append(tuple(sorted(i)))
#然后利用列表的性质去重
unique_list=list(set(sortedlist))
#打印结果
for j in unique_list:
print(j)
else:
print("Impossible.")
输入以及输出:
24
(3, 3, 7, 11)
(3, 7, 7, 7)
(3, 5, 5, 11)
(5, 5, 7, 7)
(2, 2, 3, 17)
(3, 3, 5, 13)
(2, 2, 7, 13)
36
(3, 5, 11, 17)
(5, 7, 7, 17)
(2, 2, 3, 29)
(3, 3, 11, 19)
(5, 5, 7, 19)
(5, 5, 13, 13)
(7, 7, 11, 11)
(3, 7, 13, 13)
(5, 7, 11, 13)
(3, 7, 7, 19)
(3, 5, 5, 23)
(3, 3, 7, 23)
(3, 3, 13, 17)
(2, 2, 13, 19)
46
(2, 2, 11, 31)
(5, 7, 17, 17)
(5, 5, 17, 19)
(2, 2, 5, 37)
(5, 11, 13, 17)
(3, 5, 19, 19)
(3, 7, 13, 23)
(7, 11, 11, 17)
(3, 3, 3, 37)
(3, 3, 11, 29)
(3, 11, 13, 19)
(7, 7, 13, 19)
(3, 3, 17, 23)
(2, 2, 13, 29)
(3, 5, 7, 31)
(11, 11, 11, 13)
(2, 2, 19, 23)
(5, 5, 13, 23)
(3, 7, 7, 29)
(5, 5, 5, 31)
(5, 5, 7, 29)
(5, 7, 11, 23)
(3, 7, 17, 19)
(5, 11, 11, 19)但是题目只要求我们打印一种情况就可以了,意思就是找到一个结果就里面结束遍历。
4.代码(题目结果代码)
#encoding=utf-8
#利用欧拉筛 快速筛选包含n的n以内的所有素数
def euler_sieve(n):
primes=[]
status = [False] * 2 + [True] * (n - 1)
for i in range(2,n+1):
if status[i]:
primes.append(i)
for pj in primes:
if pj * i >n:
break
status[pj*i]= False
if i % pj == 0:
break
return primes
#主程序
while True:
#n表示输入的数
n=int(input())
#kk用来接收欧拉筛出的素数表
kk=euler_sieve(n)
#asn用来存储所有可能的结果
asn=[]
#found=1表示找到了解
found=0
#遍历素数表 下面的遍历思想和m=sqrt(n)的思想是一致的
for p1 in kk:
if p1 > n//4 +1:
break
for p2 in kk:
if p2 >(n-p2)//3 +1:
break
for p3 in kk:
if p3>(n-p1-p2)//2 +1:
break
p4=n-p1-p2-p3
if p4 in kk:
print(p1,p2,p3,p4)
found=True
break
if found:
break
if found:
break
if not found:
print("Impossible.")
输出结果:

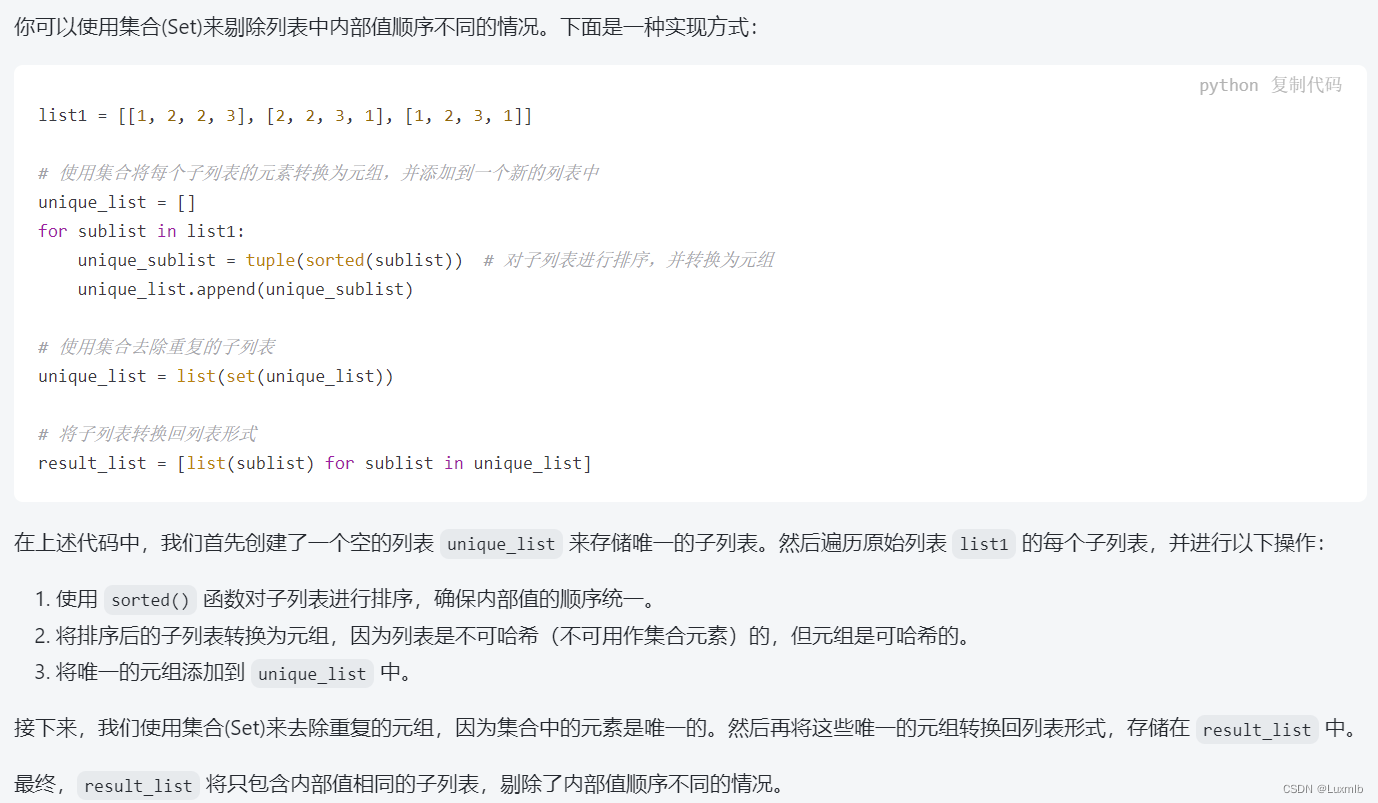
5.需要注意的地方
使用集合来剔除重复元素组的情况