LeetCode 1143.最长公共子序列

链接：1143.最长公共子序列

思路：

这题和上一题718. 最长重复子数组非常的像，唯一的区别就是这里的子序列可以不是连续的，既然不要求连续，我们可以在定义下标的时候不限制以特定字母结尾定义下标：dp[i][j]表示以长度为[0,i]的text1和长度为[0,j]的text2的最长公共子序列的长度，同样的我们有递推公式：dp[i][j] = dp[i-1][j-1] + 1，那是因为长度为i和j的字符串的最长公共子序列，可以由长度为i-1和j-1的字符串，各添加一个相同的字符得到。

除此之外，别忘了子序列可以是不连续的，这也就意味着，来自text1的子字符串和来自text2的子字符串都是可以不连续的，当text1[i-1]和text2[j-1]不相同时，我们同时查看长度为i-2，j-1时的公共子序列，和长度为i-1,j-2时的公共子序列，并取它们的最大值，也就是dp[i][j] = max(dp[i-1][j], dp[i][j-1])，这就构成了dp[i][j]的完整的递推公式。如果这一段不好理解，可以参考下图。（摘自代码随想录）

 

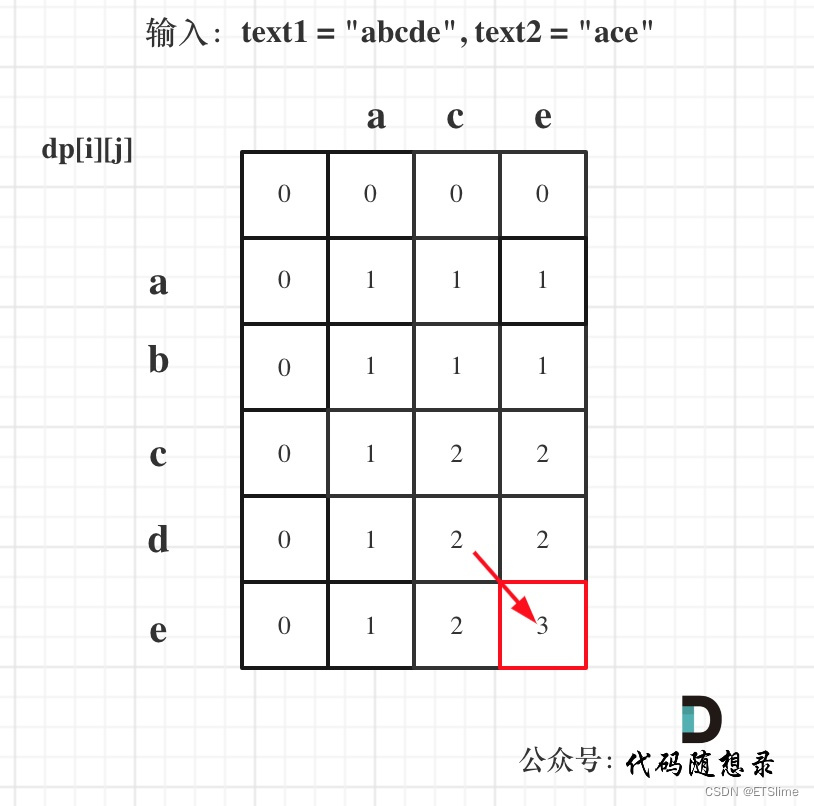
代码：

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        // 定义下标：dp[i][j]表示以长度为[0,i]的text1和长度为[0,j]的text2的最长公共子序列的长度
        vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1));
        for (int i = 1; i <= text1.size(); i++)
            for (int j = 1; j <= text2.size(); j++)
            {
                if (text1[i-1] == text2[j-1])
                    dp[i][j] = dp[i-1][j-1] + 1;
                else
                    // 关键理解这一步，当i-1和j-1不同的时候
                    // 选取i-2,j-1时的公共子序列和i-1,j-2时的公共子序列较长的那个
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
            }
        return dp[text1.size()][text2.size()];
    }
};

LeetCode 1035.不相交的线

链接：1035.不相交的线

思路：

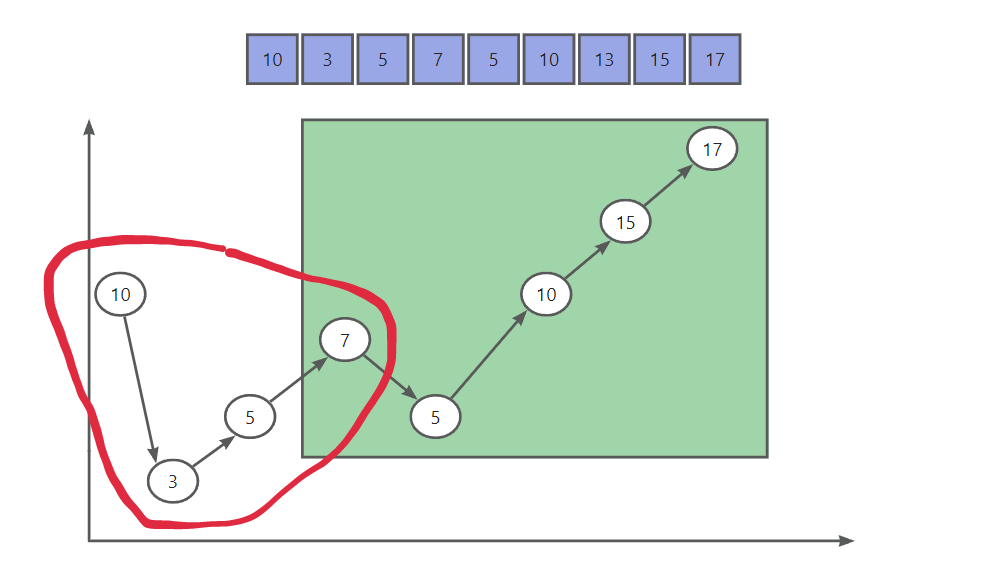
遇到相同的数组就可以用线连接起来，连线不可以交叉，求能绘制的最大连线数。只要从左端开始把两个数组一一对应的数连接起来，连线数即为最大数目，这道题目做法和上一题是完全一样的，本质上都是求相同子序列，并且可以是不连续的，几乎不用改动任何一点，代码直接照搬过来就可以了。

代码：

class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        // 定义下标:：dp[i][j]表示长度为[0, i-1]的nums1的子数列和长度为[0, j-1]的nums2的子数列所能绘制的连线数
        vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1));
        for (int i = 1; i <= nums1.size(); i++)
            for (int j = 1; j <= nums2.size(); j++)
            {
                if (nums1[i-1] == nums2[j-1])
                    dp[i][j] = dp[i-1][j-1] + 1;
                else
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
            }
        return dp[nums1.size()][nums2.size()];
    }
};

LeetCode 53. 最大子序和

链接：53. 最大子序和

思路：

这道题目之前用贪心的方法做过，思路是遍历数组然后不断累加元素，同时记录下累加过的元素的最大和，当累加元素为负，就从下一个元素重新开始累加，这题用动态规划的方法也是类似的思路。首先定义下标：dp[i]表示以nums[i]结尾的最大子数组的和，然后初始化dp[0]为数组里的第一个数nums[0]，并且用一个变量来记录当前dp数组里的最大值，然后遍历数组。递推公式为：dp[i] = max(dp[i-1] + nums[i], nums[i])。这表示以nums[i]结尾的最大子数组的和等于，以nums[i-1]结尾的最大子数组的和dp[i-1]加上nums[i]，和nums[i]本身的值，选取一个较大的，并记录下dp数组里的最大值。这个递推公式和贪心法的思路基本一致，都是累计数组里的元素，只不过动态规范的做法里，把累计的值记录在了dp数组里，然后如果上一个累加的值为负，也就是dp[i-1] + nums[i] 小于 nums[i]的情况，这个时候dp[i-1]一定小于0，这个时候要选取nums[i]作为dp[i]，并重新累加。我们可以发现递推公式只用到了dp数组里的上一个元素dp[i-1]，优化掉内存后做法其实就和贪心法一样了。

代码：

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        // 定义下标：dp[i]表示以nums[i]结尾的最大子数组的和
        vector<int> dp(nums.size());
        dp[0] = nums[0];
        int ans = dp[0];
        for (int i = 1; i < nums.size(); i++)
        {
            dp[i] = max(dp[i-1] + nums[i], nums[i]);
            ans = max(ans, dp[i]);
        }
        return ans;
    }
};