笔者自述:
一直有一个声音也一直能听到身边的大佬经常说,要把算法学习搞好,一定要重视平时的算法学习,虽然每天也在学算法,但是感觉自己一直在假装努力表面功夫骗了自己,没有规划好自己的算法学习和总结,因为后半年也该找实习了,所以每日的算法题要进行恶补,勤能补拙,因此有了这一个算法日记系列;
必读: 大佬你好,感谢您的阅读,这篇文章是我的算法笔记,方便我每日回顾;
为了不耽误您的时间,我把本篇日记的考点方向和算法知识总结列出来,如果对您有需要就继续向下进行阅读
也希望对您有帮助,和您一起通关算法!致谢

算法语言:java
题目来源:力扣–书本–初级算法,可以在力扣中搜索相关题名找到更多解法和大神方法
本文知识点:
- Hashset和Hashmap讲解
HashSet讲解: 不允许有重复元素,内部无序,由散列表实现,支持快速的查询,插入和删除。
适用场景:需要去除重复元素,不需要有序遍历元素,对元素的增删改查时间复杂度要求是O(1)情况
方法: set.add() set.delete() set.contains() set.size()
缺点:因为无序,所有空间利用率较低,最坏情况,所有元素映射到同一个散列桶内,时间复杂度退化为O(n)
HashMap讲解:键值对形式,允许空建和空值,根据键值快速查找,最优情况增删改查为O(1)
适用场景:根据键值快速增删改查,需要快速遍历映射表中的所有元素,时间复杂度最优为O(1)
方法:map.put(key,value) map.remove(key) map.containsKey(key) map.size() 遍历映射:遍历map中的key结合或者entry集合
缺点:在最坏情况下(所有键值都映射到同一个散列桶中),HashMap的时间复杂度将退化至O(N)。HashMap的性能取决于散列函数的质量。散列函数越好,冲突的概率就越低,HashMap的性能就越好
- 对于区间求数范围,可以使用二分法来确定区间的左右边界,因为二分法每次只能确定一个边界,所有可以使用两次二分法来确定左右边界
- 二叉搜索树: 左分支小于根节点,有分支大于根节点
文章目录
- 剑指 Offer 03. 数组中重复的数字
- 剑指 Offer 53 - I. 在排序数组中查找数字 I
- 剑指 Offer 53 - II. 0~n-1 中缺失的数字
- 剑指 Offer 04. 二维数组中的查找
剑指 Offer 03. 数组中重复的数字
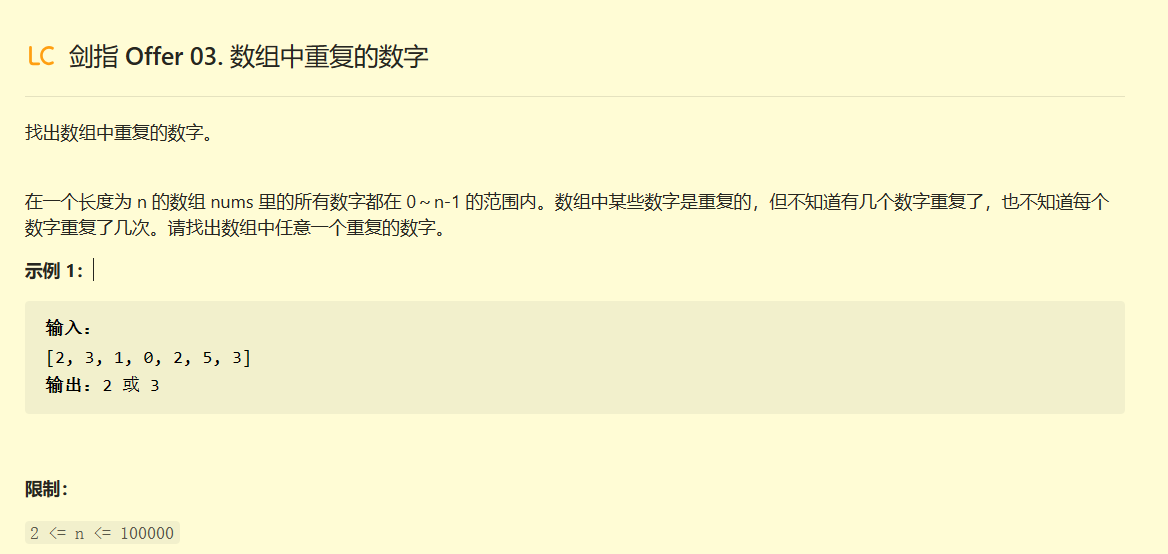
代码:
class Solution {
public int findRepeatNumber1(int[] nums){
HashMap<Integer,Integer> map = new HashMap<>();
for(int i:nums){
if(map.containsKey(i)){
return i;
}else{
map.put(i,1);
}
}
return -1;
}
// 使用hashset 遇到相同的直接返回
public int findRepeatNumber2(int[] nums){
Set<Integer> dic = new HashSet<>();
for(int num: nums){
if(dic.contains(num)) return num;
dic.add(num);
}
return -1;
}
//交换值,相当于hashmap的作用 充分使用题中的条件
public int findRepeatNumber(int[] nums){
int i =0;
while(i<nums.length){
if(nums[i] == i){
i++;
continue;
}
if(nums[nums[i]] == nums[i]) return nums[i];
int tmp = nums[i];
nums[i] = nums[tmp];
nums[tmp] = tmp;
}
return -1;
}
}
学到的知识:
- Hashset和Hashmap讲解
HashSet讲解: 不允许有重复元素,内部无序,由散列表实现,支持快速的查询,插入和删除。
适用场景:需要去除重复元素,不需要有序遍历元素,对元素的增删改查时间复杂度要求是O(1)情况
方法: set.add() set.delete() set.contains() set.size()
缺点:因为无序,所有空间利用率较低,最坏情况,所有元素映射到同一个散列桶内,时间复杂度退化为O(n)
HashMap讲解:键值对形式,允许空建和空值,根据键值快速查找,最优情况增删改查为O(1)
适用场景:根据键值快速增删改查,需要快速遍历映射表中的所有元素,时间复杂度最优为O(1)
方法:map.put(key,value) map.remove(key) map.containsKey(key) map.size() 遍历映射:遍历map中的key结合或者entry集合
缺点:在最坏情况下(所有键值都映射到同一个散列桶中),HashMap的时间复杂度将退化至O(N)。HashMap的性能取决于散列函数的质量。散列函数越好,冲突的概率就越低,HashMap的性能就越好
剑指 Offer 53 - I. 在排序数组中查找数字 I
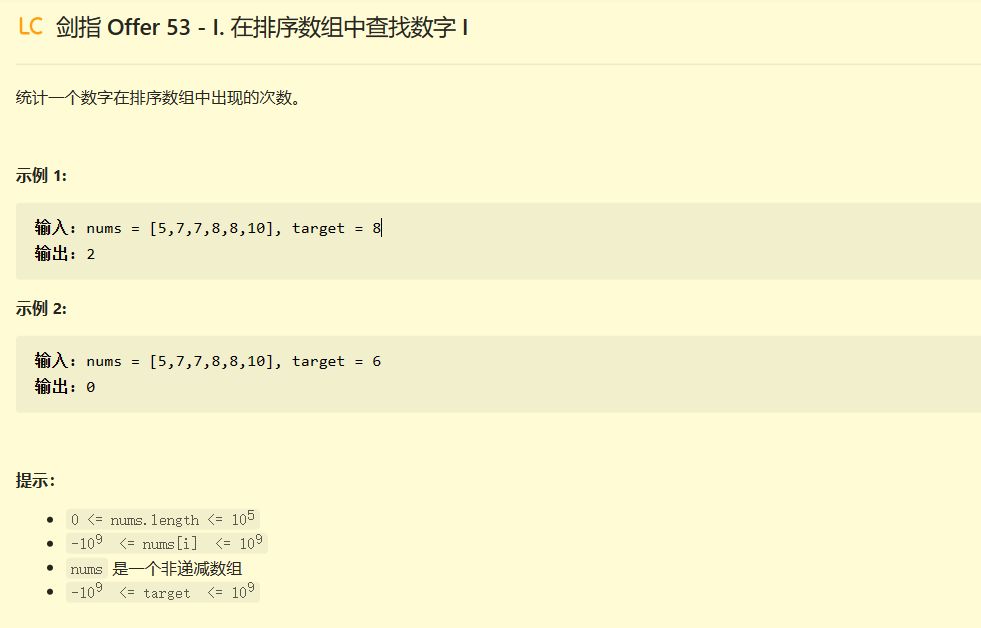
代码:
class Solution {
//使用二分法来进行查找目标值 因为二分法一次智能找到一个值
//如果要求范围的话 使用两次二分法来找到左右边界
public int search1(int[] nums, int target) {
if (nums.length <= 0) {
return 0;
}
int left = 0, right = nums.length - 1;
// 寻找左边界
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
if (left >= nums.length || nums[left] != target) {
// 如果找到的位置越界或者不是目标元素,则不存在目标元素
return 0;
}
int left1 = left;
left = 0;
right = nums.length - 1;
// 寻找右边界
while (left <= right) {
int mid = left + ((right - left) >> 1);
if (nums[mid] > target) {
right = mid - 1;
} else {
left = mid + 1;
}
}
int right1 = right;
return right1 - left1 + 1;
}
//方法二:使用hashmap来进行次数统计
public int search(int[] nums,int target){
HashMap<Integer,Integer> map = new HashMap<>();
for (int num : nums) {
if (map.containsKey(num))
map.put(num, map.get(num)+1);
else
map.put(num, 1);
}
for(int i=0;i<map.size();i++){
if(map.containsKey(target)){
return map.get(target);
}
}
return 0;
}
}
学到的知识:
- 使用hashmap操作利用键值对的对应关系来存储次数,根据条件输出,很好的练手题
- 因为是排好序的,要求个数,可以求一个区间,使用二分查找找符合规定的数,因为二分查找一次只能找到一个数,所以使用两次二分来分别找到对应的左右边界,通过索引差就可以得到想要的数据。
剑指 Offer 53 - II. 0~n-1 中缺失的数字
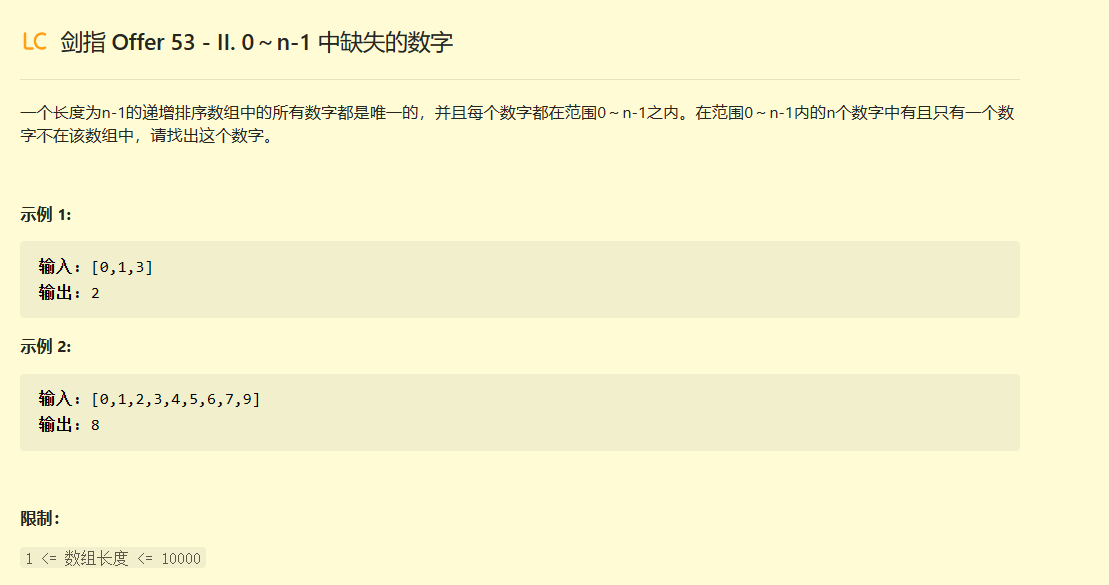
代码:
class Solution {
public int missingNumber1(int[] nums){
//求和
int sum = 0;
int sum1 =0;
for(int i =0;i<nums.length;i++){
sum += nums[i];
}
for(int i =1;i<=nums.length;i++){
sum1 +=i;
}
return sum1-sum;
}
//使用hashmap解决
public int missingNumber2(int[] nums){
HashMap<Integer,Integer> map = new HashMap<>();
int length = nums.length;
for(int i =0;i<nums.length;i++){
map.put(nums[i],1);
}
for(int i =0;i<=nums.length;i++){
if(!map.containsKey(i))
return i;
}
return 0;
}
public int missingNumber(int[] nums){
if(nums.length<=0){
return 0;
}
int xor = 0;
for(int i =0;i<nums.length;i++){
xor = xor^nums[i]^(i+1);
}
return xor;
}
}
学到的知识:
- 位运算真的很快,学会利用位运算很大程度上降低时间复杂度,上述我实现了三个方法,其中哈希表的时间复杂度最高,但是最容易理解,这道题我做了第二次了,拿到后思路仍然很凌乱,首先想到的是使用哈希表来解决问题,位运算挺好的,要多练习。
剑指 Offer 04. 二维数组中的查找
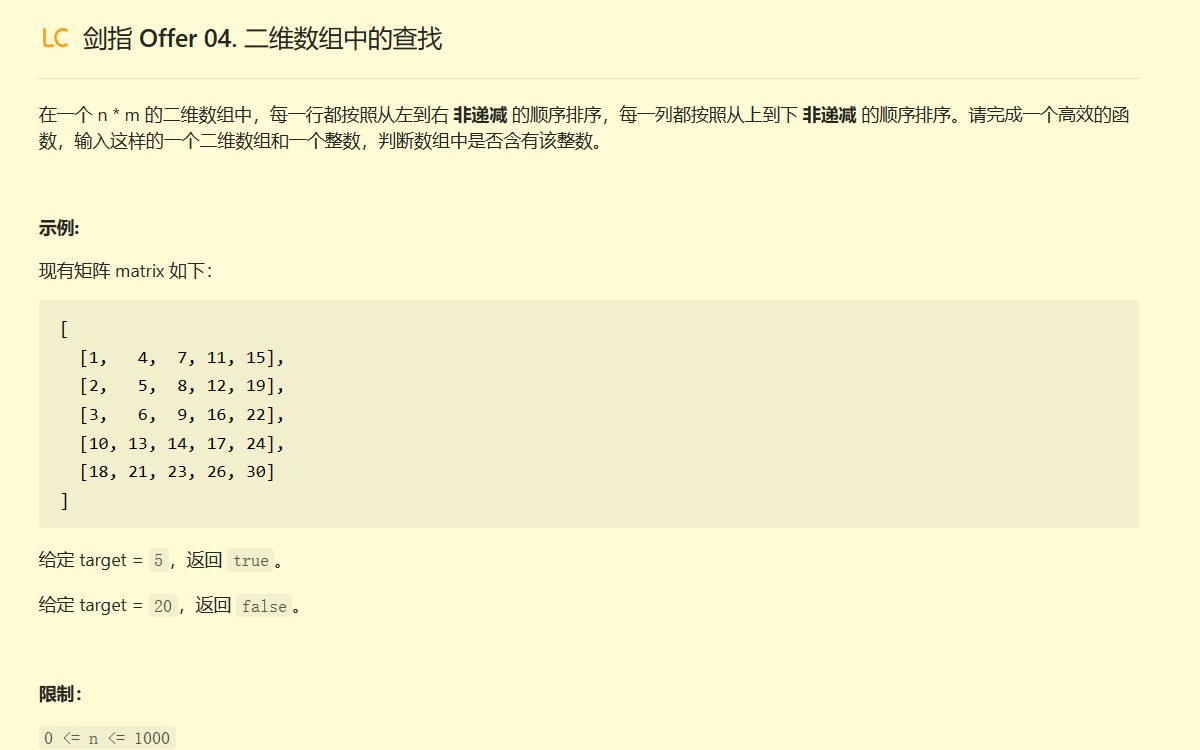
代码:
public boolean findNumberIn2DArray(int[][] matrix,int target){
//使用双层for循环 可以求出 时间复杂度太高
// 如何搜索 通过比对 范围 时间复杂度为O(N*M)
boolean flag ;
for(int i =0;i<matrix.length;i++){
for(int j =0;j<matrix[0].length;j++){
if(target == matrix[i][j]){
return true;
}
}
}
return false;
}
//使用二叉树的方法来进行实现
public boolean findNumberIn2DArray1(int[][] matrix,int target){
int i = matrix.length-1,j =0;
while(i>=0&& j<matrix[0].length){
if (matrix[i][j] >target){
i--;
}else if(matrix[i][j] <target){
j++;
}else{
return true;
}
}
return false;
}
学到的知识:
- 二叉搜索树: 左分支小于根节点,有分支大于根节点
可以通过二叉搜索的方式来找到目标值,通过移动i和j;同时也可以直接使用暴力方法来进行寻找。