在这里插入图片描述
【深度学习入门到进阶】必看系列，含激活函数、优化策略、损失函数、模型调优、归一化算法、卷积模型、序列模型、预训练模型、对抗神经网络等

在这里插入图片描述
专栏详细介绍：【深度学习入门到进阶】必看系列，含激活函数、优化策略、损失函数、模型调优、归一化算法、卷积模型、序列模型、预训练模型、对抗神经网络等

本专栏主要方便入门同学快速掌握相关知识。后续会持续把深度学习涉及知识原理分析给大家，让大家在项目实操的同时也能知识储备，知其然、知其所以然、知何由以知其所以然。

声明：部分项目为网络经典项目方便大家快速学习，后续会不断增添实战环节（比赛、论文、现实应用等）

专栏订阅：

深度学习入门到进阶专栏
深度学习应用项目实战篇

深度学习实践篇[17]：模型压缩技术、模型蒸馏算法：Patient-KD、DistilBERT、DynaBERT、TinyBERT

1.模型压缩概述

1.2模型压缩原有

理论上来说，深度神经网络模型越深，非线性程度也就越大，相应的对现实问题的表达能力越强，但相应的代价是，训练成本和模型大小的增加。同时，在部署时，大模型预测速度较低且需要更好的硬件支持。但随着深度学习越来越多的参与到产业中，很多情况下，需要将模型在手机端、IoT端部署，这种部署环境受到能耗和设备体积的限制，端侧硬件的计算能力和存储能力相对较弱，突出的诉求主要体现在以下三点：

首先是速度，比如像人脸闸机、人脸解锁手机等应用，对响应速度比较敏感，需要做到实时响应。
其次是存储，比如电网周边环境监测这个应用场景中，要图像目标检测模型部署在可用内存只有200M的监控设备上，且当监控程序运行后，剩余内存会小于30M。
最后是耗能，离线翻译这种移动设备内置AI模型的能耗直接决定了它的续航能力。

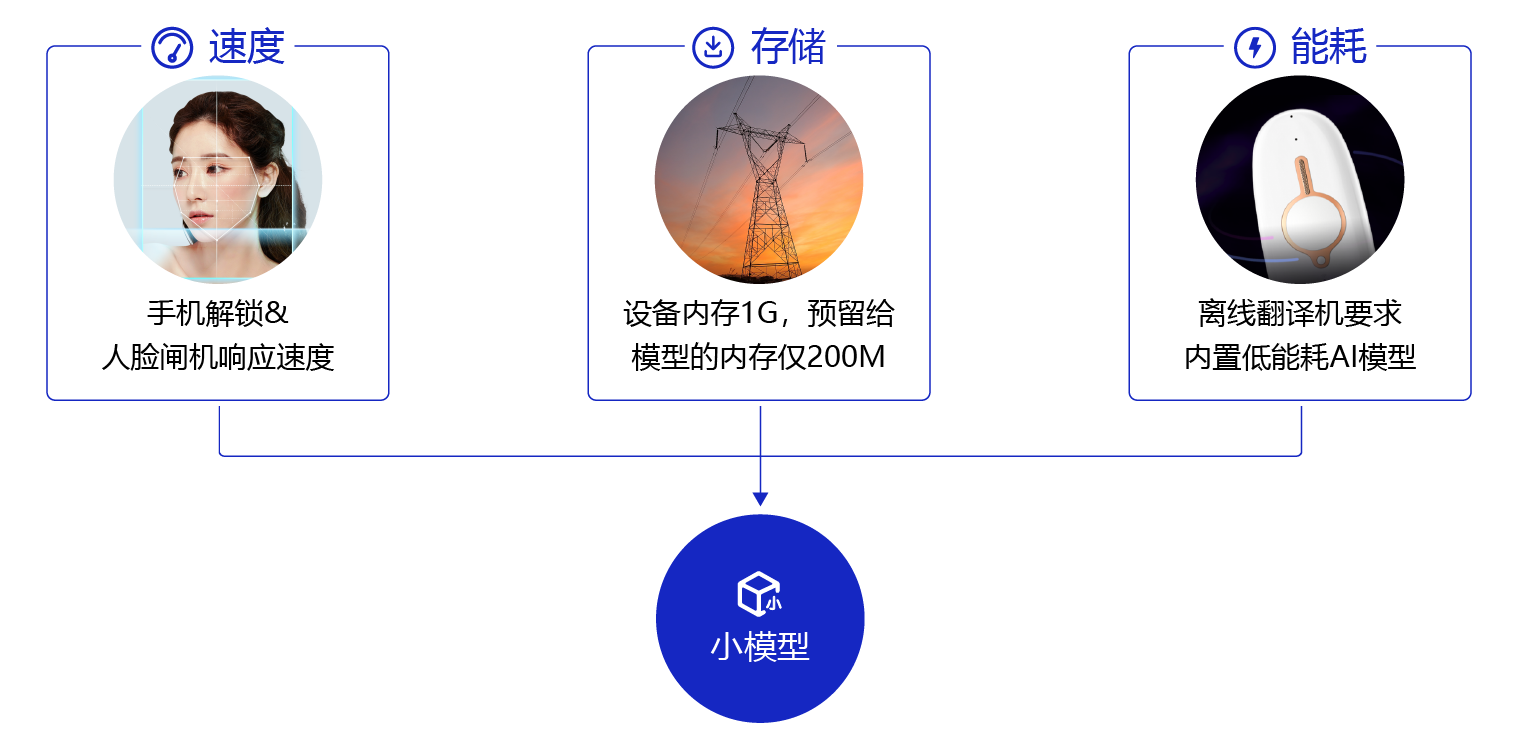
以上三点诉求都需要我们根据终端环境对现有模型进行小型化处理，在不损失精度的情况下，让模型的体积更小、速度更快，能耗更低。

但如何能产出小模型呢？常见的方式包括设计更高效的网络结构、将模型的参数量变少、将模型的计算量减少，同时提高模型的精度。可能有人会提出疑问，为什么不直接设计一个小模型？要知道，实际业务子垂类众多，任务复杂度不同，在这种情况下，人工设计有效小模型难度非常大，需要非常强的领域知识。而模型压缩可以在经典小模型的基础上，稍作处理就可以快速拔高模型的各项性能，达到“多快好省”的目的。

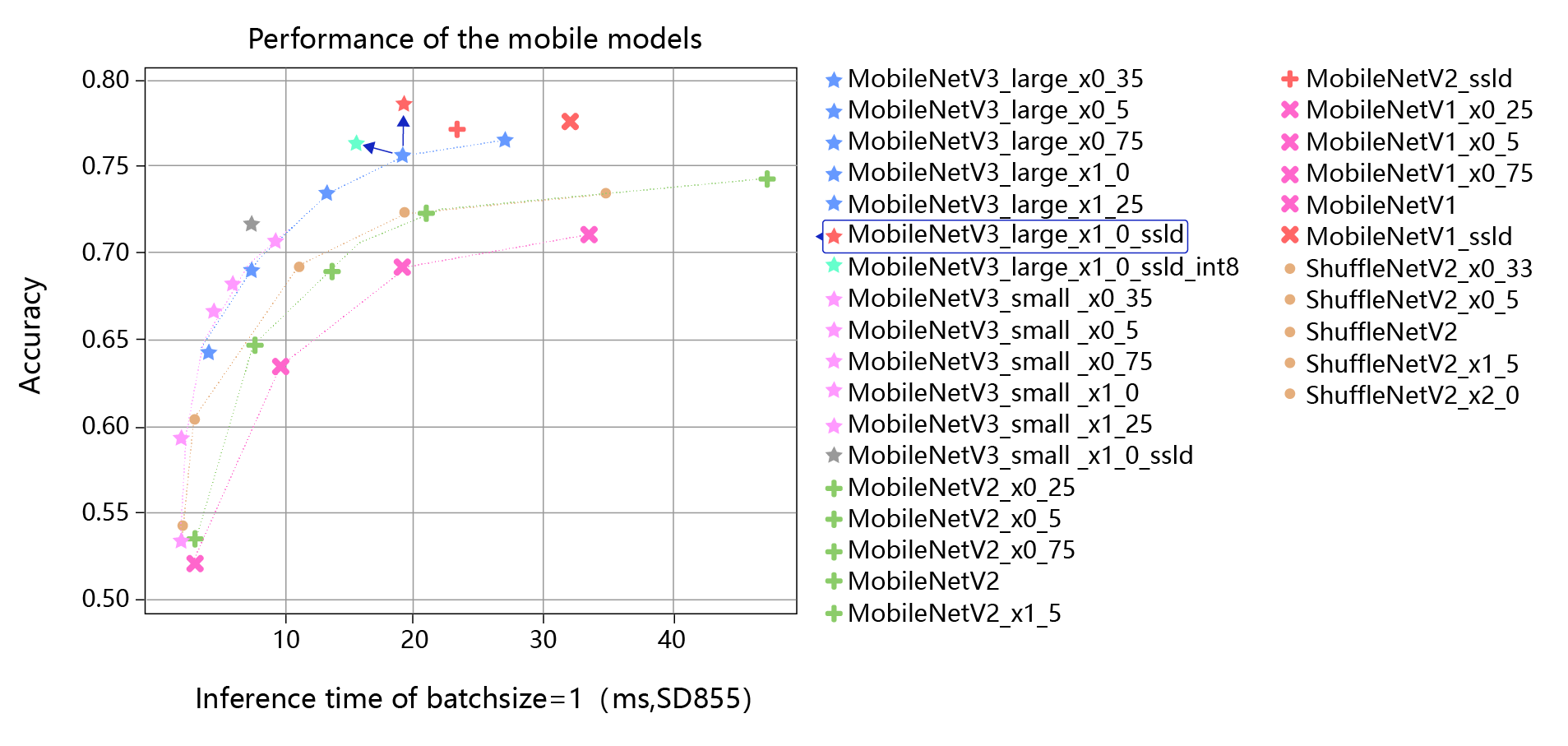
上图是分类模型使用了蒸馏和量化的效果图，横轴是推理耗时，纵轴是模型准确率。图中最上边红色的星星对应的是在MobileNetV3_large model基础上，使用蒸馏后的效果，相比它正下方的蓝色星星，精度有明显的提升。图中所标浅蓝色的星星，对应的是在MobileNetV3_large model基础上，使用了蒸馏和量化的结果，相比原始模型，精度和推理速度都有明显的提升。可以看出，在人工设计的经典小模型基础上，经过蒸馏和量化可以进一步提升模型的精度和推理速度。

1.2.模型压缩的基本方法

模型压缩可以通过以下几种方法实现：

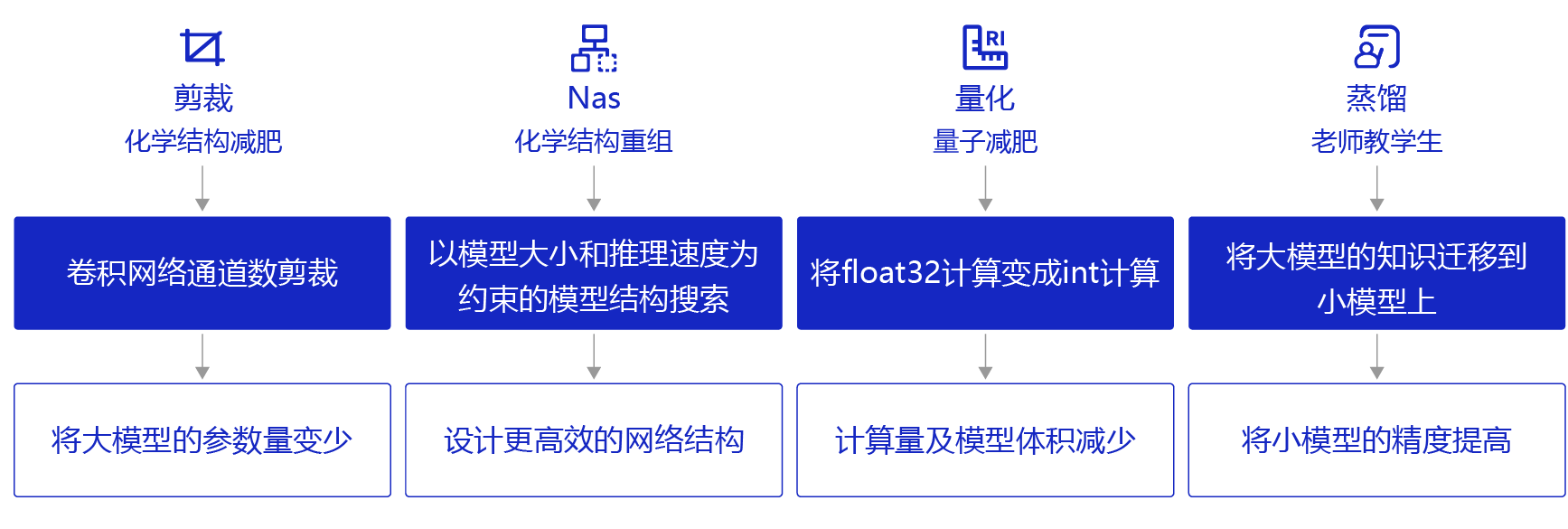
剪裁：类似“化学结构式的减肥”，将模型结构中对预测结果不重要的网络结构剪裁掉，使网络结构变得更加 ”瘦身“。比如，在每层网络，有些神经元节点的权重非常小，对模型加载信息的影响微乎其微。如果将这些权重较小的神经元删除，则既能保证模型精度不受大影响，又能减小模型大小。
量化：类似“量子级别的减肥”，神经网络模型的参数一般都用float32的数据表示，但如果我们将float32的数据计算精度变成int8的计算精度，则可以牺牲一点模型精度来换取更快的计算速度。
蒸馏：类似“老师教学生”，使用一个效果好的大模型指导一个小模型训练，因为大模型可以提供更多的软分类信息量，所以会训练出一个效果接近大模型的小模型。
神经网络架构搜索（NAS）：类似“化学结构式的重构”，以模型大小和推理速度为约束进行模型结构搜索，从而获得更高效的网络结构。

除此以外，还有权重共享、低秩分解等技术也可实现模型压缩。

2.Patient-KD 模型蒸馏

2.1. Patient-KD 简介

论文地址：Patient Knowledge Distillation for BERT Model Compression

图1: Vanilla KD和PKD比较

BERT预训练模型对资源的高需求导致其很难被应用在实际问题中，为缓解这个问题，论文中提出了Patient Knowledge Distillation（Patient KD）方法，将原始大模型压缩为同等有效的轻量级浅层网络。同时，作者对以往的知识蒸馏方法进行了调研，如图1所示，vanilla KD在QNLI和MNLI的训练集上可以很快的达到和teacher model相媲美的性能，但在测试集上则很快达到饱和。对此，作者提出一种假设，在知识蒸馏的过程中过拟合会导致泛化能力不良。为缓解这个问题，论文中提出一种“耐心”师生机制，即让Patient-KD中的学生模型从教师网络的多个中间层进行知识提取，而不是只从教师网络的最后一层输出中学习。

2.2. 模型实现

Patient-KD中提出如下两个知识蒸馏策略：

PKD-Skip: 从每k层学习，这种策略是假设网络的底层包含重要信息，需要被学习到（如图2a所示）
PKD-last: 从最后k层学习，假设教师网络越靠后的层包含越丰富的知识信息（如图2b所示）

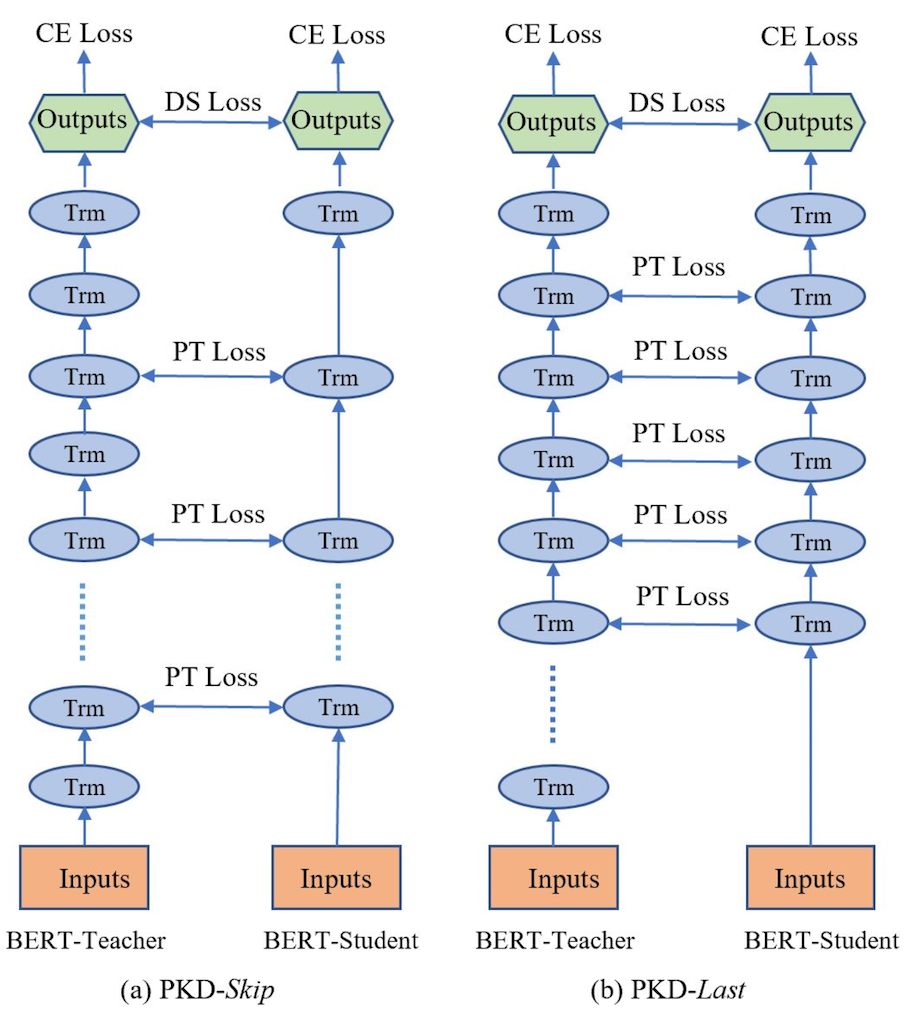
图2a: PKD-Skip 学生网络学习教师网络每两层的输出图2b: PKD-Last 学生网络从教师网络的最后六层学习

因为在BERT中仅使用最后一层的[CLS] token的输出来进行预测，且在其他BERT的变体模型中，如SDNet，是通过对每一层的[CLS] embedding的加权平均值进行处理并预测。由此可以推断，如果学生模型可以从任何教师网络中间层中的[CLS]表示中学习，那么它就有可能获得类似教师网络的泛化能力。

因此，Patient-KD中提出特殊的一种损失函数的计算方式：

$L_{PT} = \sum_{i=1}^{N}\sum_{j=1}^{M} \left \| \frac{h_{i,j}^s}{\left \| h_{i,j}^s \right \|_{2}} - \frac{h_{i, I_{pt}(j)}^t}{\left \| h_{i, I_{pt}(j)}^t \right \|_2}\right \|_2^2$

其中，对于输入 $x_i$ ，所有层的[CLS]的输出表示为：

$h_i = [h_{i,1}, h_{i,2},..., h_{i,k}] = BERT_{k}(x_i) \in \mathbb{R}^{k\times d}$
$I_{pt}$ 表示要从中提取知识的一组中间层，以从 $BERT_{12}$ 压缩到 $BERT_6$ 为例，对于PKD-Skip策略， $I_{pt} = {2,4,6,8,10}$ ；对于PKD-Last策略， $I_{pt} = {7,8,9,10,11}$ 。M表示学生网络的层数，N是训练样本的数量，上标s和t分别代表学生网络和教师网络。

同时，Patient-KD中也使用了 $L_{DS}$ 和 $L_{CE}^S$ 两种损失函数用来衡量教师和学生网络的预测值的距离和学生网络在特定下游任务上的交叉熵损失。

$L_{DS}=-\sum_{i \in [N]} \sum_{c \in C}[P^t(y_i = c|x_i;\hat{\theta}^t)\cdot log P^s(y_i = c |x_i; \theta^s)]$

$L_{CE}^s=-\sum_{i \in [N]} \sum_{c \in C}\mathbb{1}[y_i=c]\cdot log P^s(y_i = c|x_i;\theta^s)]$

最终的目标损失函数可以表示为：

$L_{PKD} = (1-\alpha)L_{CE}^S+\alpha L_{DS} + \beta L_{PT}$

2.3. 实验结果

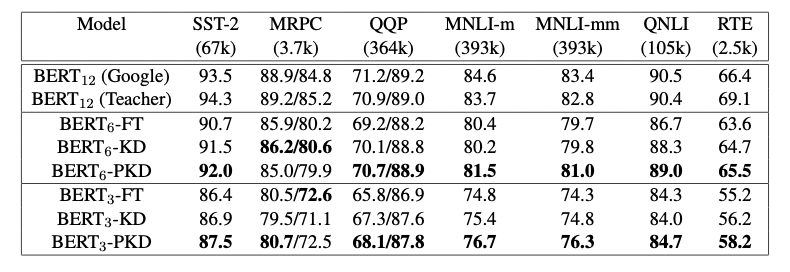
图3: results from the GLUE test server

作者将模型预测提交到GLUE并获得了在测试集上的结果，如图3所示。与fine-tuning和vanilla KD这两种方法相比，使用PKD训练的 $BERT_3$ 和 $BERT_6$ 在除MRPC外的几乎所有任务上都表现良好。其中，PKD代表Patient-KD-Skip方法。对于MNLI-m和MNLI-mm，六层模型比微调（FT）基线提高了1.1%和1.3%，

我们将模型预测提交给官方 GLUE 评估服务器以获得测试数据的结果。结果总结在表 1 中。与直接微调和普通 KD 相比，我们使用 BERT3 和 BERT6 学生的 Patient-KD 模型在除 MRPC 之外的几乎所有任务上都表现最好。此外，6层的 $BERT_{6}-PKD$ 在7个任务中有5个都达到了和BERT-Base相似的性能，其中，SST-2（与 BERT-Base 教师相比为-2.3%）、QQP（-0.1%）、MNLI-m（-2.2%）、MNLI-mm（-1.8%）和 QNLI (-1.4%))，这五个任务都有超过6万个训练样本，这表明了PKD在大数据集上的表现往往更好。

图4: PKD-Last 和 PKD-Skip 在GLUE基准上的对比

尽管这两种策略都比vanilla KD有所改进，但PKD-Skip的表现略好于PKD-Last。作者推测，这可能是由于每k层的信息提炼捕获了从低级到高级的语义，具备更丰富的内容和更多不同的表示，而只关注最后k层往往会捕获相对同质的语义信息。

图5: 参数量和推理时间对比

图5展示了 $BERT_3$ 、 $BERT_6$ 、 $BERT_12$ 的推理时间即参数量, 实验表明Patient-KD方法实现了几乎线性的加速， $BERT_6$ 和 $BERT_3$ 分别提速1.94倍和3.73倍。

3.DistilBERT蒸馏

3.1. DistilBERT 简介

论文地址：DistilBERT, a distilled version of BERT: smaller, faster, cheaper and lighter

图1: 几个预训练模型的参数量统计

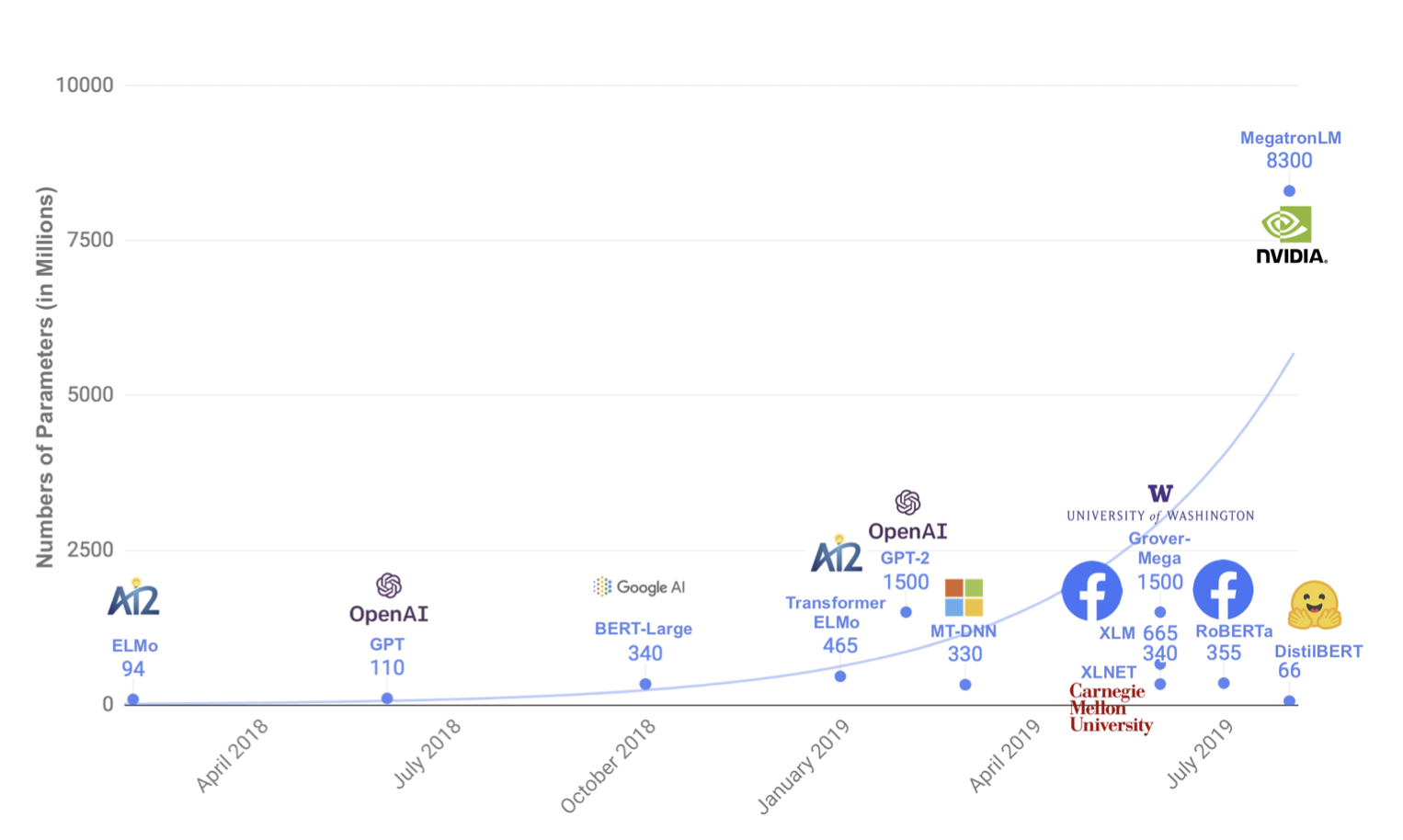
近年来，大规模预训练语言模型成为NLP任务的基本工具，虽然这些模型带来了显著的改进，但它们通常拥有数亿个参数（如图1所示），而这会引起两个问题。首先，大型预训练模型需要的计算成本很高。其次，预训练模型不断增长的计算和内存需求可能会阻碍语言处理应用的广泛落地。因此，作者提出DistilBERT，它表明小模型可以通过知识蒸馏从大模型中学习，并可以在许多下游任务中达到与大模型相似的性能，从而使其在推理时更轻、更快。

3.2. 模型实现

学生网络结构

学生网络DistilBERT具有与BERT相同的通用结构，但token-type embedding和pooler层被移除，层数减半。学生网络通过从教师网络中每两层抽取一层来进行初始化。

Training loss

$L_{ce}$ 训练学生模仿教师模型的输出分布：

$L_{ce} = \sum_i t_i * log(s_i)$
其中， $t_i$ 和 $s_i$ 分别是教师网络和学生网络的预测概率。

同时使用了Hinton在2015年提出的softmax-temperature：

$p_i = \frac{exp(z_i/T)}{\sum_j exp(z_j/T)}$
其中， $T$ 控制输出分布的平滑度，当T变大时，类别之间的差距变小；当T变小时，类别间的差距变大。 $z_i$ 代表分类 $i$ 的模型分数。在训练时对学生网络和教师网络使用同样的temperature $T$ ，在推理时，设置 $T = 1$ ，恢复为标准的softmax
最终的loss函数为 $L_{ce}$ 、Mask language model loss $L_{mlm}$ （参考BERT）和 cosine embedding loss $L_{cos}$ （student和teacher隐藏状态向量的cos计算）的线性组合。

3.3. 实验结果

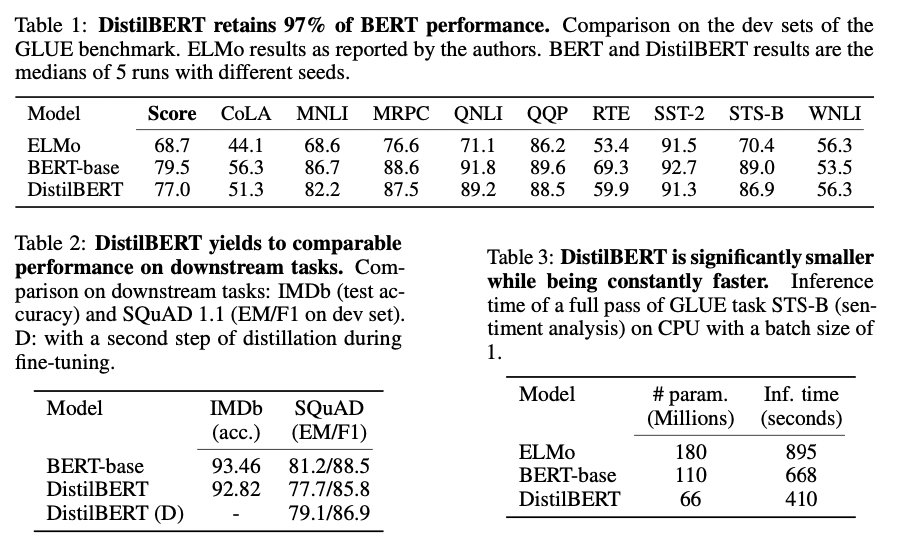
图2：在GLUE数据集上的测试结果、下游任务测试和参数量对比

根据上图我们可以看到，DistilBERT与BERT相比减少了40%的参数，同时保留了BERT 97%的性能，但提高了60%的速度。

4.DynaBERT蒸馏

4.1. DynaBERT 简介

论文地址：DynaBERT: Dynamic BERT with Adaptive Width and Depth

预训练模型，如BERT，在自然语言处理任务中的强大之处是毫无疑问，但是由于模型参数量较多、模型过大等问题，在部署方面对设备的运算速度和内存大小都有着极高的要求。因此，面对实际产业应用时，比如将模型部署到手机上时，就需要对模型进行瘦身压缩。近年的模型压缩方式基本上都是将大型的BERT网络压缩到一个固定的小尺寸网络。而实际工作中，不同的任务对推理速度和精度的要求不同，有的任务可能需要四层的压缩网络而有的任务会需要六层的压缩网络。DynaBERT（dynamic BERT）提出一种不同的思路，它可以通过选择自适应宽度和深度来灵活地调整网络大小，从而得到一个尺寸可变的网络。

4.2. 模型实现

DynaBERT的训练阶段包括两部分，首先通过知识蒸馏的方法将teacher BERT的知识迁移到有自适应宽度的子网络student $DynaBERT_W$ 中，然后再对 $DynaBERT_W$ 进行知识蒸馏得到同时支持深度自适应和宽度自适应的子网络 DynaBERT。训练过程流程图如图1所示。

图1： DynaBERT的训练过程

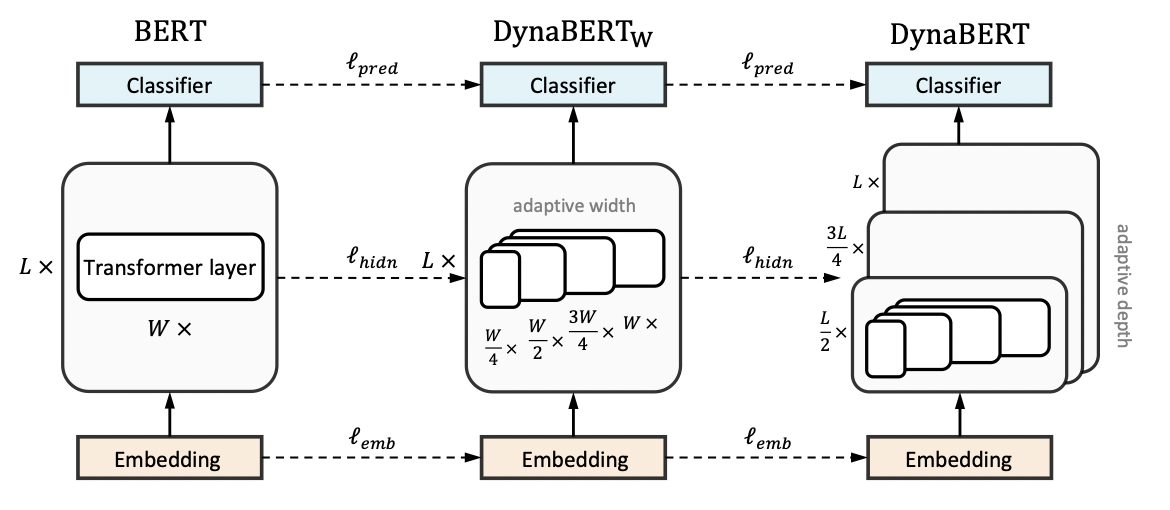
宽度自适应 Adaptive Width

一个标准的transfomer中包含一个多头注意力（MHA）模块和一个前馈网络（FFN）。在论文中，作者通过变换注意力头的个数 $N_h$ 和前馈网络中中间层的神经元个数 $d_{ff}$ 来更改transformer的宽度。同时定义一个缩放系数 $m_w$ 来进行剪枝，保留MHA中最左边的 $m_wN_H]$ 个注意力头和 FFN中 $m_wd_{ff}]$ 个神经元。

为了充分利用网络的容量，更重要的头部或神经元应该在更多的子网络中共享。因此，在训练宽度自适应网络前，作者在 fine-tuned BERT网络中根据注意力头和神经元的重要性对它们进行了排序，然后在宽度方向上以降序进行排列。这种选取机制被称为 Network Rewiring。

图2: Network Rewiring

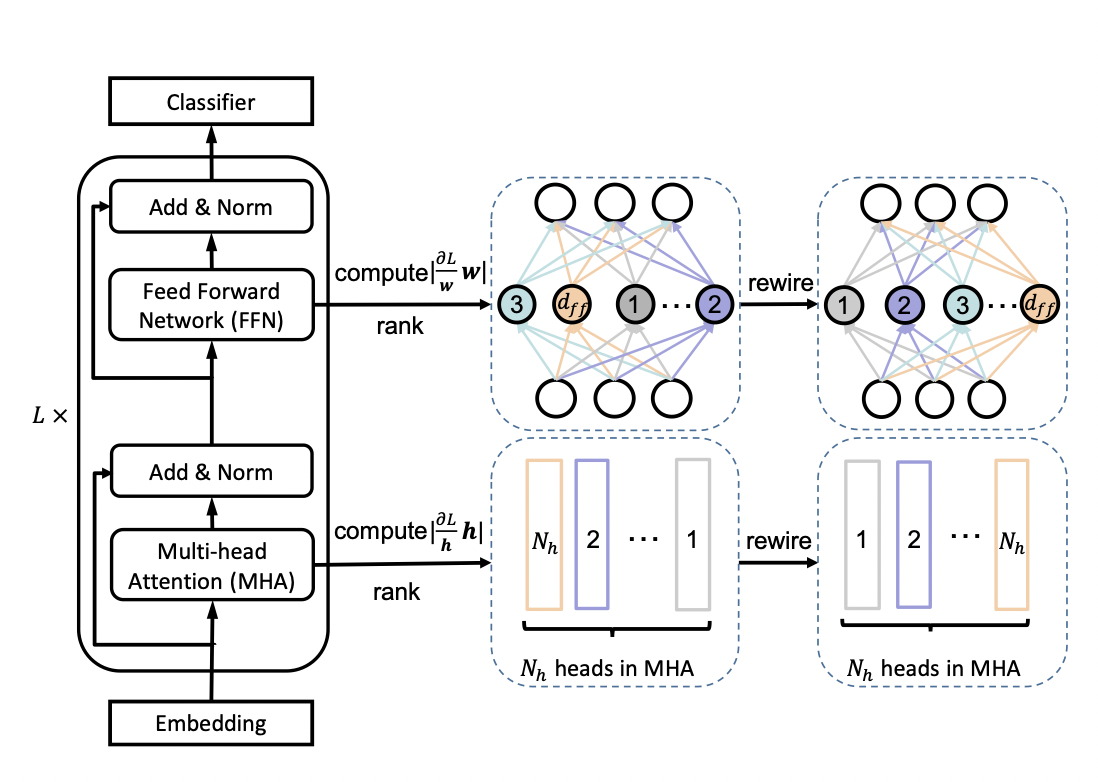
那么，要如何界定注意力头和神经元的重要性呢？作者参考 P. Molchanov et al., 2017 和 E. Voita et al., 2019 两篇论文提出，去掉某个注意力头或神经元前后的loss变化，就是该注意力头或神经元的重要程度，变化越大则越重要。

训练宽度自适应网络

首先，将BERT网络作为固定的教师网络，并初始化 $DynaBERT_W$ 。然后通过知识蒸馏将知识从教师网络迁移到 $DynaBERT_W$ 中不同宽度的学生子网络。其中， $m_w = [1.0, 0.75, 0.5, 0.25]$ 。

模型蒸馏的loss定义为：

$\lambda_1l_{pred}(y^{(m_w)}, y) + \lambda_2(l_{emb}(E^{(m_w)},E) + l_{hidn}(H^{(m_w)}, H))$

其中， $\lambda_1, \lambda_2$ 是控制不同损失函数权重的参数， $l_{pred}, l_{emb}, l_{hidn}$ 分别定义为：

$\begin{align} l_{pred}(y^{(m_w)}, y) &= SCE(y^{(m_w)}, y), \\ l_{emb}(E^{(m_w)}, E) &= MSE(E^{(m_w)}, E), \\ l_{hidn}(H^{(m_w)}, H) &= \sum^{L}_{l=1} MSE(H^{(m_w)}_l, H_l) \\ \end{align}$

$l_{pred}$ 代表预测层的loss，SCE 代表交叉熵损失函数。 $l_{emb}$ 代表嵌入层的loss，MSE代表均方差损失函数。 $l_{hidn}$ 则为隐藏层的loss。

训练深度自适应网络

训练好宽度自适应的 $DynaBERT_W$ 后，就可以将其作为教师网络训练同时具备宽度自适应和深度自适应的DynaBERT了。为了避免宽度方向上的灾难性遗忘，在每一轮训练中，仍对不同宽度进行训练。深度调节系数 $m_d$ 对网络层数进行调节，在训练中定义 $m_d = [1.0, 0.75, 0.5]$ 。深度方向上的剪枝根据 $\frac{1}{m_d}) = 0$ 来去掉特定层。

模型蒸馏的loss定义为：

$\lambda_1l^{'}_{pred}(y^{(m_w,m_d)},y^{(m_w)}) + \lambda_2(l^{'}_{emb}(E^{(m_w,m_d)},E^{(m_w)}+l^{'}_{hidn}(H^{(m_w,m_d)},H^{(m_w)}))$

4.3. 实验结果

根据不同的宽度和深度剪裁系数，作者最终得到12个大小不同的DyneBERT模型，其在GLUE上的效果如下：

图3: results on GLUE benchmark

图4:Comparison of #parameters, FLOPs, latency on GPU and CPU between DynaBERT and DynaRoBERTa and other methods.

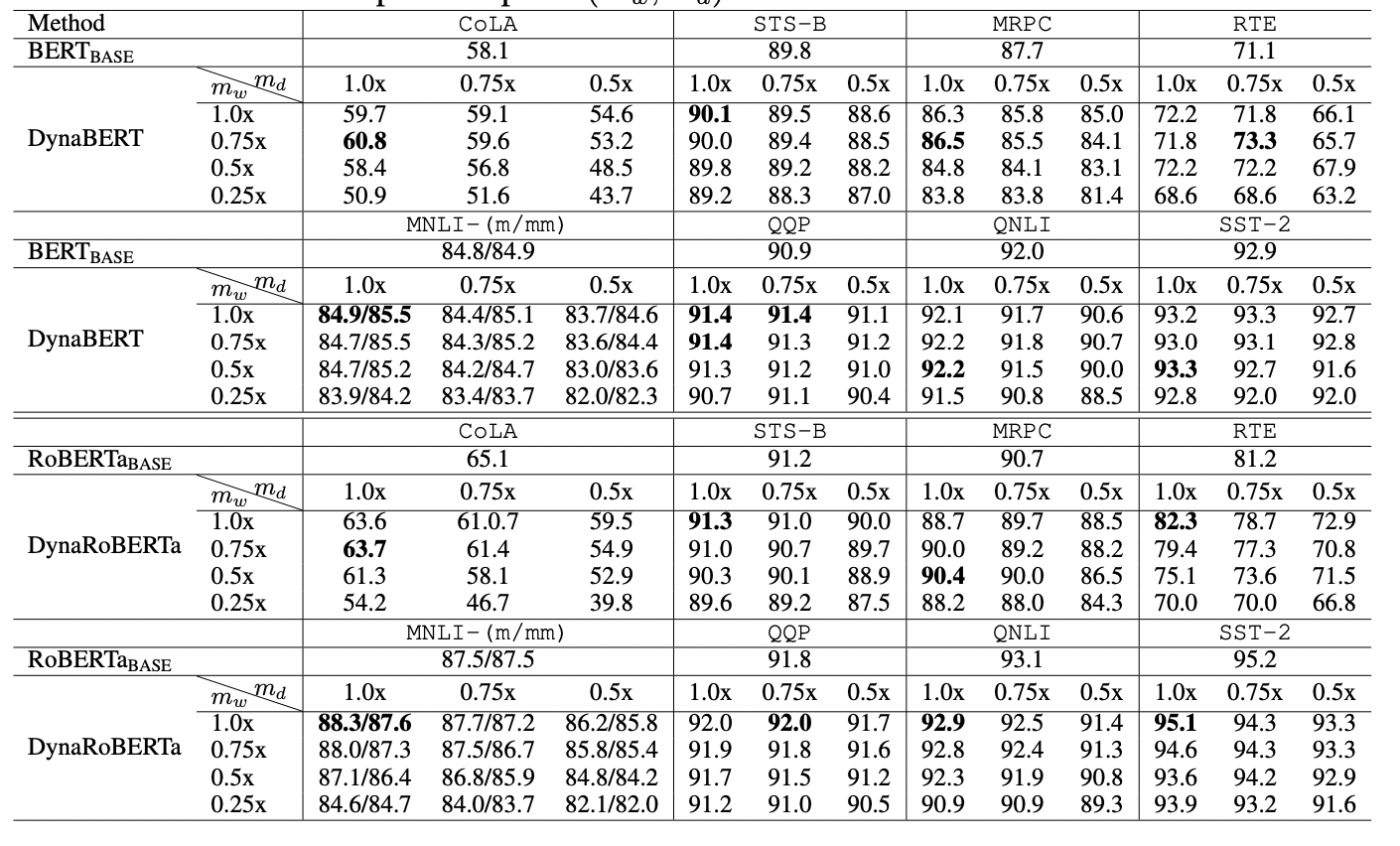
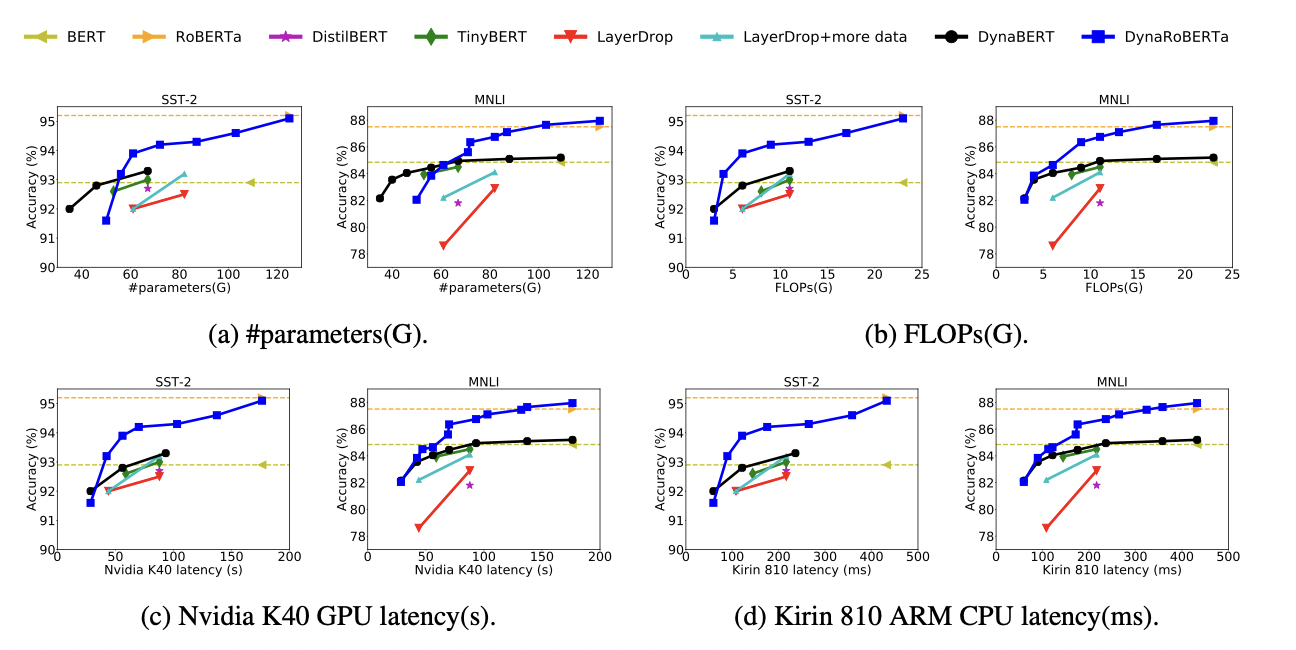
可以看到论文中提出的DynaBERT和DynaRoBERTa可以达到和 $BERT_{BASE}$ 及 $Dy na R o BERT a$ 相当的精度，但是通常包含更少的参数，FLOPs或更低的延迟。在相同效率的约束下，从DynaBERT中提取的子网性能优于DistilBERT和TinyBERT。

5.TinyBERT 蒸馏

5.1. TinyBERT 简介

论文地址：TinyBERT: Distilling BERT for Natural Language Understanding

预训练模型的提出，比如BERT，显著的提升了很多自然语言处理任务的表现，它的强大是毫无疑问的。但是他们普遍存在参数过多、模型庞大、推理时间过长、计算昂贵等问题，因此很难落地到实际的产业应用中。TinyBERT是由华中科技大学和华为诺亚方舟实验室联合提出的一种针对transformer-based模型的知识蒸馏方法，以BERT为例对大型预训练模型进行研究。四层结构的 $TinyBERT_{4}$ 在 GLUE benchmark 上可以达到 $BERT_{base}$ 96.8%及以上的性能表现，同时模型缩小7.5倍，推理速度提升9.4倍。六层结构的 $TinyBERT_{6}$ 可以达到和 $BERT_{base}$ 同样的性能表现。

图1: TinyBERT learning

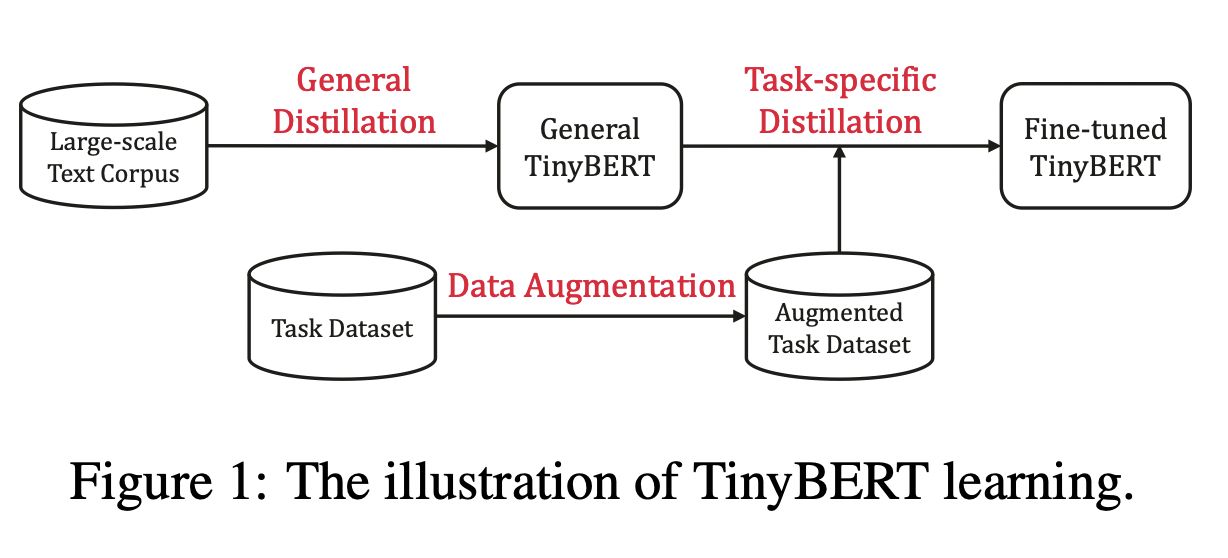
TinyBERT主要做了以下两点创新：

提供一种新的针对 transformer-based 模型进行蒸馏的方法，使得BERT中具有的语言知识可以迁移到TinyBERT中去。
提出一个两阶段学习框架，在预训练阶段和fine-tuning阶段都进行蒸馏，确保TinyBERT可以充分的从BERT中学习到一般领域和特定任务两部分的知识。

5.2. 模型实现

5.2.1知识蒸馏

知识蒸馏的目的在于将一个大型的教师网络 $T$ 学习到的知识迁移到小型的学生网络 $S$ 中。学生网络通过训练来模仿教师网络的行为。 $f^S$ 和 $f^T$ 代表教师网络和学生网络的behavior functions。这个行为函数的目的是将网络的输入转化为信息性表示，并且它可被定义为网络中任何层的输出。在基于transformer的模型的蒸馏中，MHA（multi-head attention）层或FFN（fully connected feed-forward network）层的输出或一些中间表示，比如注意力矩阵 $A$ 都可被作为行为函数使用。

$L_{KD} = \sum_{x \in X}L(f^S(x), f^T(x))$

其中 $L(\cdot)$ 是一个用于评估教师网络和学生网络之间差异的损失函数， $x$ 是输入文本， $X$ 代表训练数据集。因此，蒸馏的关键问题在于如何定义行为函数和损失函数。

5.2.2 Transformer Distillation

假设TinyBert有M层transformer layer，teacher BERT有N层transformer layer，则需要从teacher BERT的N层中抽取M层用于transformer层的蒸馏。 $n = g (m)$ 定义了一个从学生网络到教师网络的映射关系，表示学生网络中第m层网络信息是从教师网络的第g(m)层学习到的，也就是教师网络的第n层。TinyBERT嵌入层和预测层也是从BERT的相应层学习知识的，其中嵌入层对应的指数为0，预测层对应的指数为M + 1，对应的层映射定义为 $0 = g (0)$ 和 $N + 1 = g (M + 1)$ 。在形式上，学生模型可以通过最小化以下的目标函数来获取教师模型的知识：

$L_{model} = \sum_{x \in X}\sum^{M+1}_{m=0}\lambda_m L_{layer}(f^S_m(x), f^T_{g(m)}(x))$

其中 $L_{layer}$ 是给定的模型层的损失函数（比如transformer层或嵌入层）， $f_m$ 代表第m层引起的行为函数， $\lambda_{m}$ 表示第m层蒸馏的重要程度。

TinyBERT的蒸馏分为以下三个部分：transformer-layer distillation、embedding-layer distillation、prediction-layer distillation。

Transformer-layer Distillation

Transformer-layer的蒸馏由attention based蒸馏和hidden states based蒸馏两部分组成。

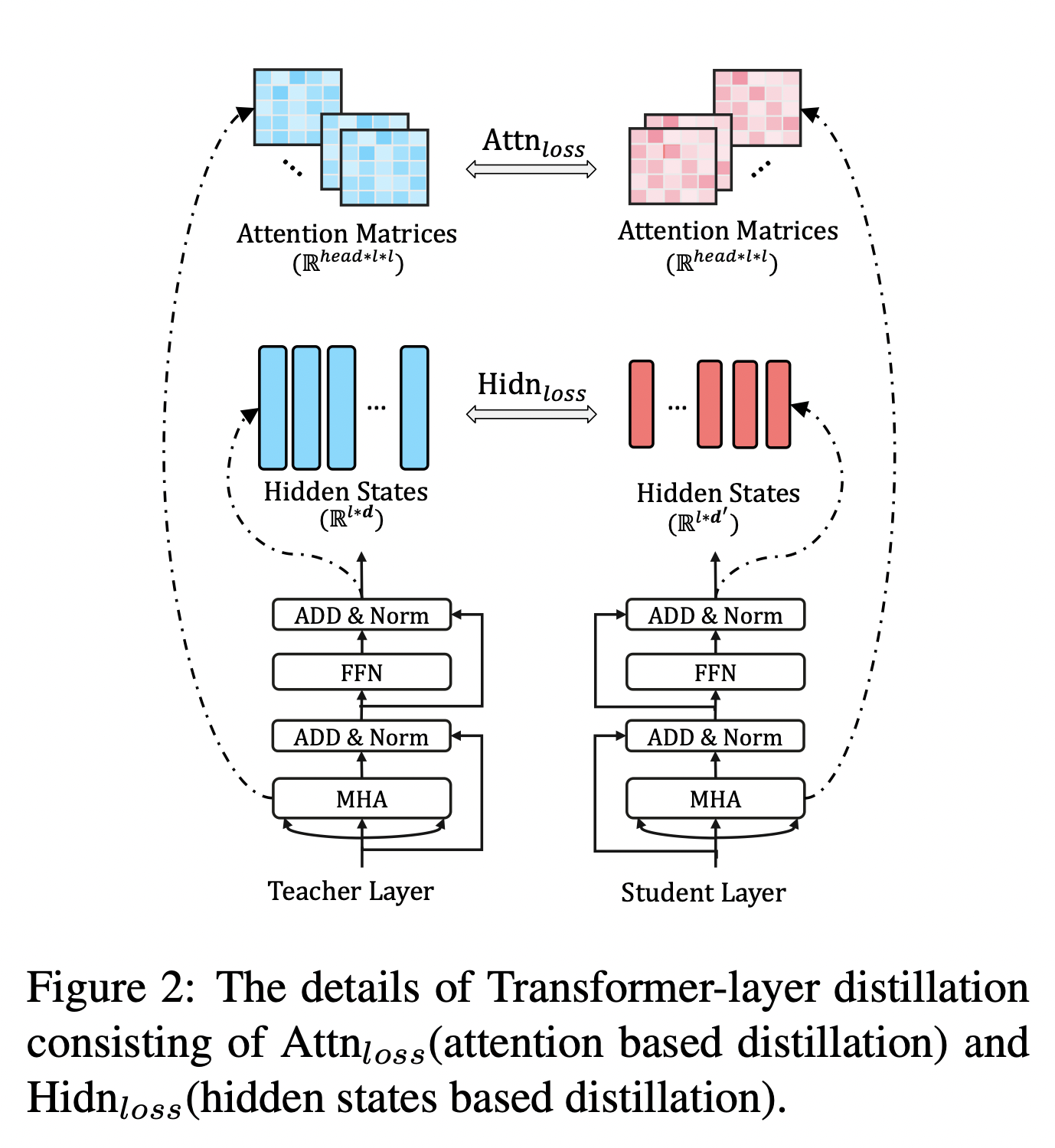
图2: Transformer-layer distillation

其中，attention based蒸馏是受到论文Clack et al., 2019的启发，这篇论文中提到，BERT学习的注意力权重可以捕获丰富的语言知识，这些语言知识包括对自然语言理解非常重要的语法和共指信息。因此，TinyBERT提出attention based蒸馏，其目的是使学生网络很好地从教师网络处学习到这些语言知识。具体到模型中，就是让TinyBERT网络学习拟合BERT网络中的多头注意力矩阵，目标函数定义如下：

$L_{attn} = \frac{1}{h}\sum^{h}_{i=1}MSE(A^S_i, A^T_i)$

其中， $h$ 代表注意力头数， $A_i \in \mathbb{R}^{l\times l}$ 代表学生或教师的第 $i$ 个注意力头对应的注意力矩阵， $l$ 代表输入文本的长度。论文中提到，使用注意力矩阵 $A$ 而不是 $so f t ma x (A)$ 是因为实验结果显示这样可以得到更快的收敛速度和更好的性能表现。

hidden states based蒸馏是对transformer层输出的知识进行了蒸馏处理，目标函数定义为：

$L_{hidn} = MSE(H^SW_h, H^T)$

其中， $H^S \in \mathbb{R}^{l \times d^{'}},\quad H^T \in \mathbb{R}^{l \times d}$ 分别代表学生网络和教师网络的隐状态，是FFN的输出。 $d$ 和 $d^{'}$ 代表教师网络和学生网络的隐藏状态大小，且 $d^{'} < d$ ，因为学生网络总是小于教师网络。 $W_h \in \mathbb{R}^{d^{'} \times d}$ 是一个可训练的线性变换矩阵，将学生网络的隐藏状态投影到教师网络隐藏状态所在的空间。

Embedding-layer Distillation

$L_{embd} = MSE(E^SW_e, E^T)$

Embedding loss和hidden states loss同理，其中 $E^S,\quad E^T$ 代表学生网络和教师网络的嵌入，他呢和隐藏状态矩阵的形状相同，同时 $W_e$ 和 $W_h$ 的作用也相同。

Prediction-layer Distillation

$L_{pred} = CE(z^T/t, z^S/t)$

其中， $z^S, \quad z^T$ 分别是学生网络和教师网络预测的logits向量， $CE$ 代表交叉熵损失， $t$ 是temperature value，当 $t = 1$ 时，表现良好。

对上述三个部分的loss函数进行整合，则可以得到教师网络和学生网络之间对应层的蒸馏损失如下：

$\begin{equation} L_{layer} = \left\{ \begin{array}{lr} L_{embd}, & m=0 \\ L_{hidn} + L_{attn}, & M \geq m > 0 \\ L_{pred}, & m = M + 1 \end{array} \right. \end{equation}$

5.3. 实验结果

图3: Results evaluated on GLUE benchmark

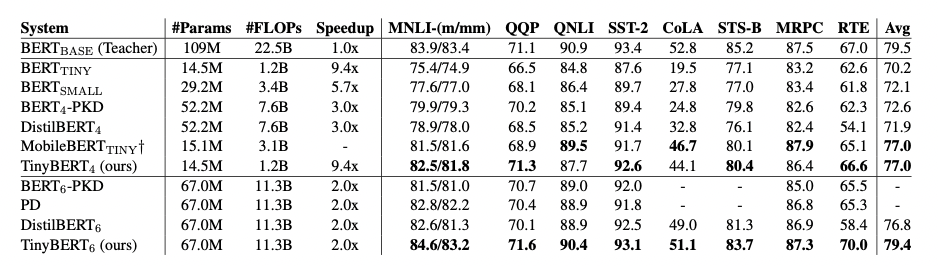
作者在GLUE基准上评估了TinyBERT的性能，模型大小、推理时间速度和准确率如图3所示。实验结果表明，TinyBERT在所有GLUE任务上都优于 $BERT_{TINY}$ ，并在平均性能上获得6.8%的提升。这表明论文中提出的知识整理学习框架可以有效的提升小模型在下游任务中的性能。同时， $TinyBERT_4$ 以~4%的幅度显著的提升了KD SOTA基准线（比如，BERT-PKD和DistilBERT），参数缩小至~28%，推理速度提升3.1倍。与teacher $BERT_{base}$ 相比，TinyBERT在保持良好性能的同时，模型缩小7.5倍，速度提升9.4倍。