常见骨干网络介绍

news2024/11/25 7:03:28

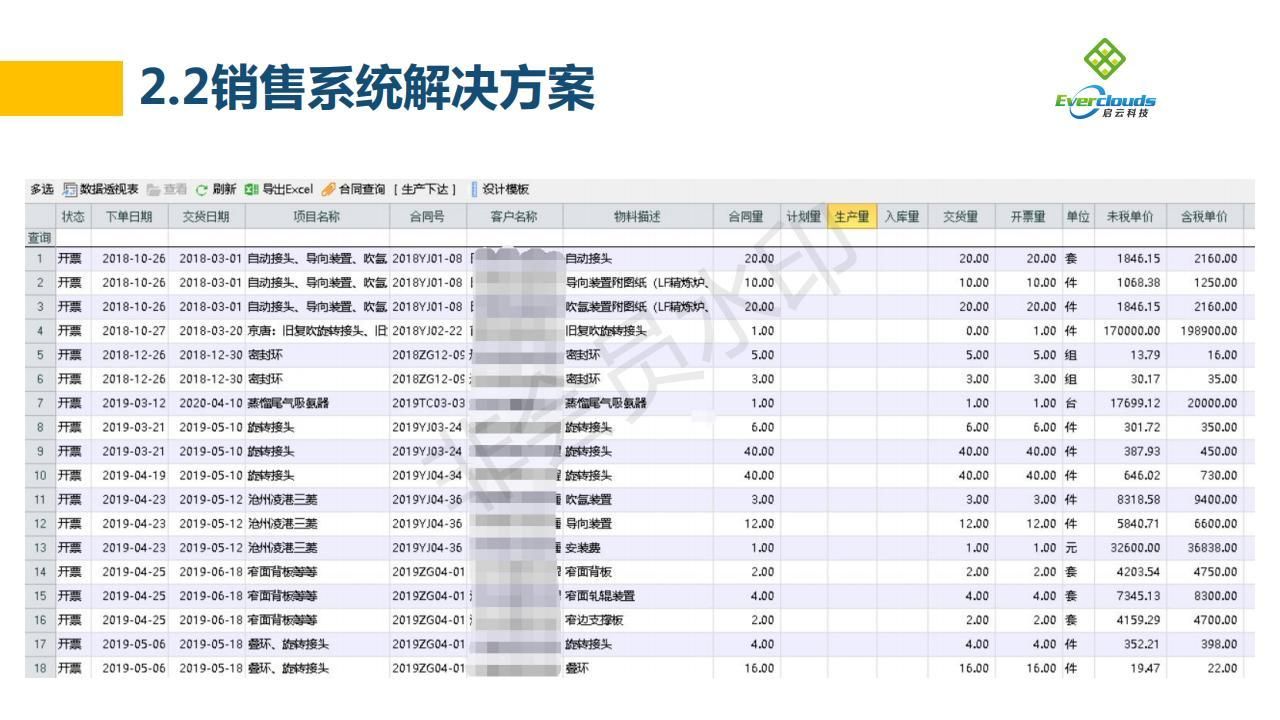
骨干网络

骨干网络（backbone network）顾名思义，是深度学习中最核心的网络组成。本文按时间顺序，简要介绍几种影响重大的backbone设计思路，我们或许可以从窥探前人的设计思路中获得启发和灵感。

1.1 AlexNet, 2012

这是2012年提出的世界上第一种深度神经网络，它率先打破了CV领域特征工程的垄断地位，以巨大优势赢得了当年ImagNet比赛。
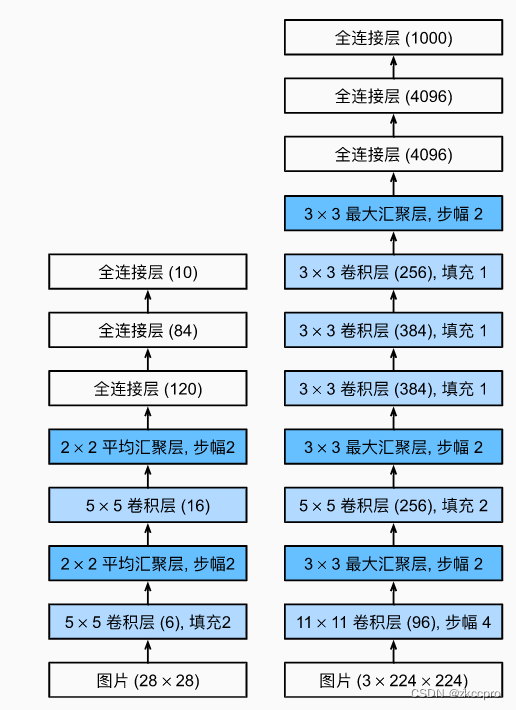
请添加图片描述
图1 LeNet（左）与AlexNet（右）网络结构

乍一看，和LeNet比好像也没啥特别的，，就是层数多了。但还有一些著名的细节技术方案在AlexNet第一次被提出或使用：

  1. 第一次采用ReLU替代sigmod作为激活函数，可以降低运算量、避免梯度消失。
  2. 在最后的全连接层使用Dropout以控制模型复杂度。
  3. 训练时采用大量的数据增强（翻转、裁剪、变色）以提高模型鲁棒性，减少过拟合。

最后，附上AlexNet的pytorch实现：

import torch
from torch import nn

net = nn.Sequential(
    # 这里，我们使用一个11*11的更大窗口来捕捉对象。
    # 同时，步幅为4，以减少输出的高度和宽度。
    # 另外，输出通道的数目远大于LeNet
    nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 减小卷积窗口，使用填充为2来使得输入与输出的高和宽一致，且增大输出通道数
    nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 使用三个连续的卷积层和较小的卷积窗口。
    # 除了最后的卷积层，输出通道的数量进一步增加。
    # 在前两个卷积层之后，汇聚层不用于减少输入的高度和宽度
    nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Flatten(),
    # 这里，全连接层的输出数量是LeNet中的好几倍。使用dropout层来减轻过拟合
    nn.Linear(6400, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    # 最后是输出层。由于这里使用Fashion-MNIST，所以用类别数为10，而非论文中的1000
    nn.Linear(4096, 10))

1.2 VGG, 2014

VGG是2014年由牛津大学提出的，它最大的改进和贡献在于以【块】为基本单位进行骨干网设计。这确实很大程度上影响了后来网络设计的思路。

VGG的提出者发现：深度卷积神经网络的基本组成无非是：

  1. 卷积层
  2. 激活函数
  3. 池化层

那好，我把这仨东西作为一个块，用这个块来堆积成网络：
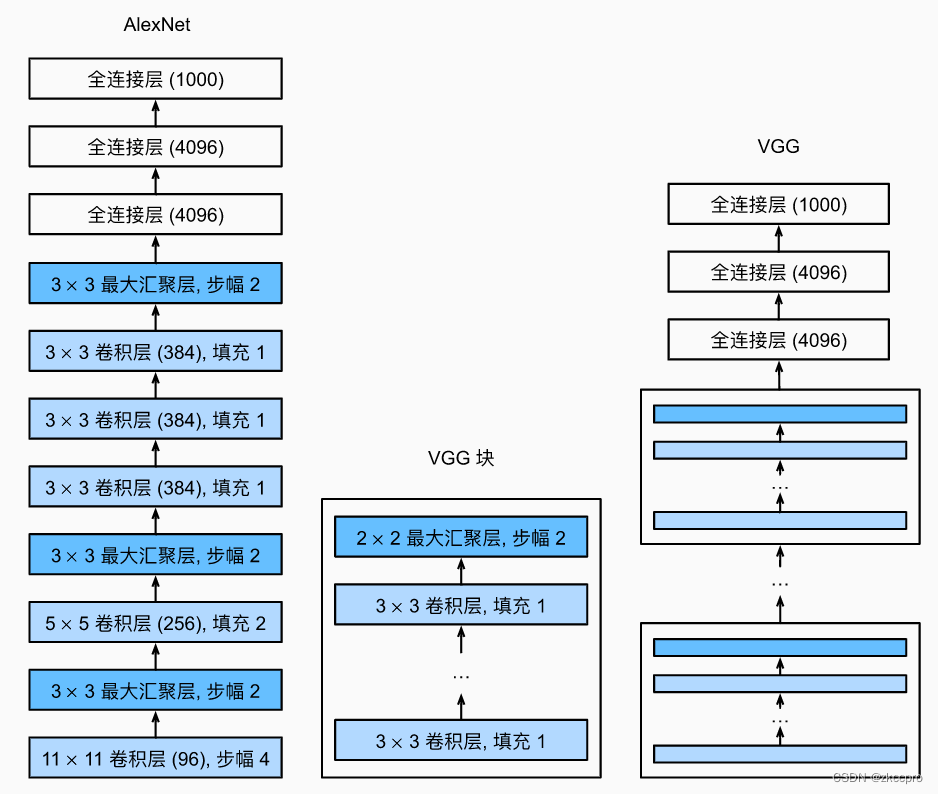
请添加图片描述
图2 AlexNet与VGG

数一数上图（右）有几层（卷积层+全连接层）？有n层我们就管这个网络叫VGG-n（比如VGG-11、VGG-19…）

1.3 GoogLeNet, 2014

VGG网络只是提出了一种规范化的深度学习网络设计思路，但确实没啥新东西出现。同样是2014年的GoogLeNet在ImageNet比赛中大获全胜，也提出了一种更有效的 Inception block：
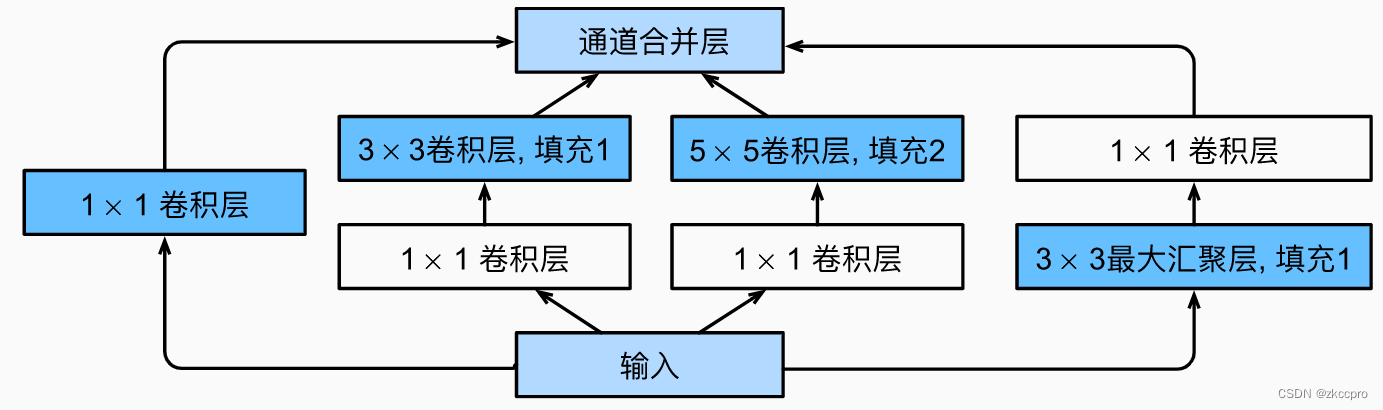
请添加图片描述
图3 Inception block

说白了这东西就是由很多不同尺寸的卷积核并联起来…以让网络自己决定到底该使用哪一种尺寸的卷积核更多一些…看起来很简单的设计，但更有效就是硬道理。

进一步地，GoogLeNet用了Inception块作为骨干网的基础组成，GoogLeNet的整体结构如下：
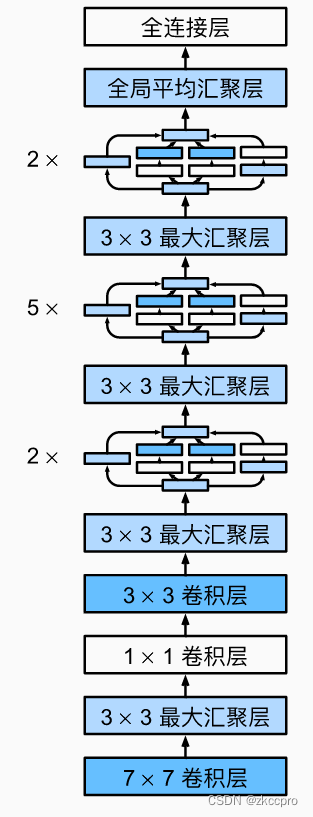
请添加图片描述
图4 GoogLeNet结构

最后，附上Inception块的pytorch实现：

import torch
from torch import nn
from torch.nn import functional as F


class Inception(nn.Module):
    # c1--c4是每条路径的输出通道数
    def __init__(self, in_channels, c1, c2, c3, c4, **kwargs):
        super(Inception, self).__init__(**kwargs)
        # 线路1，单1x1卷积层
        self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)
        # 线路2，1x1卷积层后接3x3卷积层
        self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
        # 线路3，1x1卷积层后接5x5卷积层
        self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
        # 线路4，3x3最大汇聚层后接1x1卷积层
        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)

    def forward(self, x):
        p1 = F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        # 在通道维度上连结输出
        return torch.cat((p1, p2, p3, p4), dim=1)

1.4 ResNet, 2016

ResNet可以说是里程碑式的骨干网络结构，它在2016年由何凯明、孙剑等人提出。（十分遗憾的是孙剑在2022年去世）

ResNet的提出基于这样一个【观察】：AlexNet之后，深度学习领域形成了一个信念：网络层数越深，效果越好。但[resnet]中却发现并不是这样，当网络层深达到一定程度之后，学习效果反而开始下降了，这怎么可能呢？

[resnet]中给出了自己的【分析】：你说，当n层网络能学习到一个东西的时候，那n+1层网络能不能学到这个东西？直观来说一定可以啊，因为如果n层都能办到，那只需n+1层做一个【恒等映射】不就行了吗？？？怎么会造成学习效果下降呢？？？？所以上面的观察现象很奇怪，神经网络不是可以拟合任何复杂的线性、非线性函数吗？怎么连最简单的恒等映射都实现不了呢？？？？？

紧接着，[resnet]给出了自己的【猜想】：神经网络发展到现在，或许是能拟合世界上最复杂的非线性函数，但也正因为此，它连最简单的恒等映射就是实现不了…那既然如此，我让它能实现恒等映射不就完了吗？

于是，[resnet]提出了一种【解决方案】：用残差块 提供给 层 恒等映射的能力。
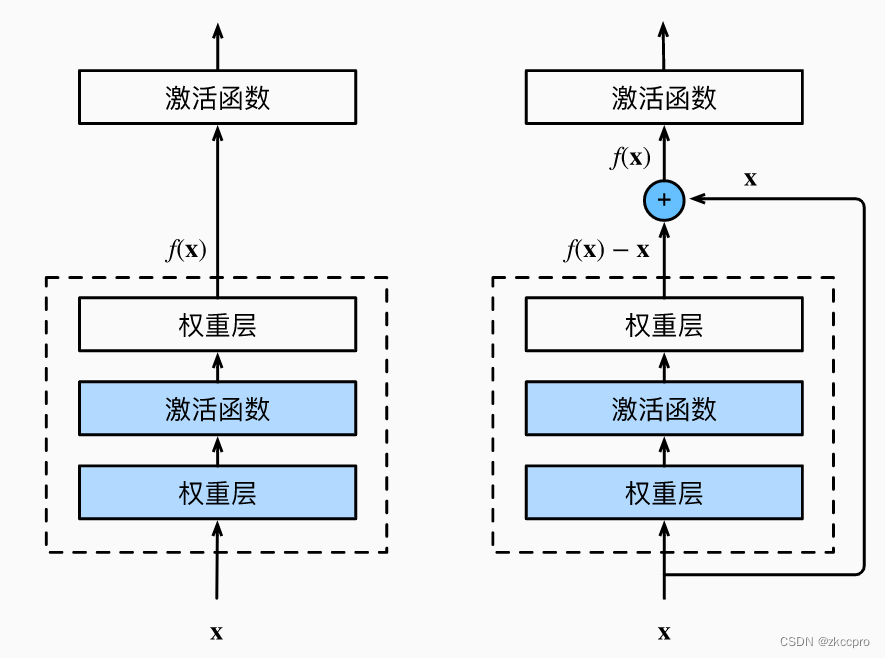
请添加图片描述
图5 正常块（左）与残差块（右）

同样，结构简洁明了，效果拔群，残差神经网络在今天（2022年）仍然是最受欢迎的骨干网方案之一。不近如此，它的设计思路也启发了后续的很多设计，还是非常伟大的。

而且其中的论文思路：【观察】、【分析】、【猜想】、【解决方案】也非常值得我们学习。

ResNet结构和其他骨干网类似，堆积残差块即可：
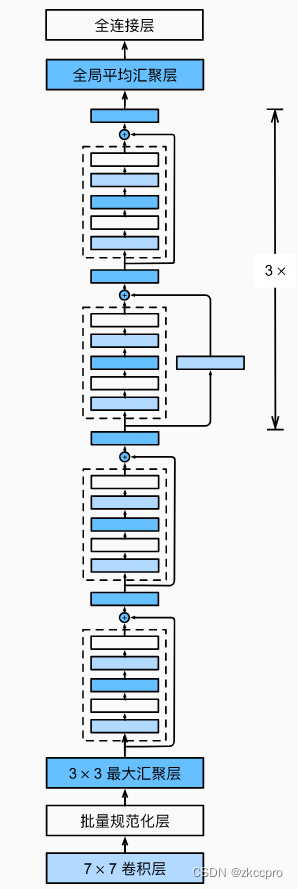
请添加图片描述
图6 ResNet结构

不仅如此，在[resnet]的工作中，还有一些细节改进：

  1. 提出并使用warmup训练策略。
  2. 在残差块中，每个卷积层后都使用了BatchNorm。（但BN不是[resnet]提出的）
  3. 还提出了一种瓶颈模块（Bottleneck Block）以降低参数量

下面附上残差块和瓶颈块具体实现，实现时还是有一些细节需要注意的：

# 网络模块接口
class BlockInterface(nn.Module):
    # 参数：输入通道数，输出通道数，是否开启BN，是否开启Dropout
    def __init__(self, input_channels, output_channels,
                BN=True, Dropout=False):
        super().__init__()
        self.input_channels = input_channels
        self.output_channels = output_channels
        self.BN = BN
        self.Dropout = Dropout

    def forward(self, x):
        pass


# 残差模块
# 参数量：input*output*3*3+output*output*3*3+input*output
class ResidualBlock(BlockInterface):
    def __init__(self, input_channels, output_channels, 
                BN=True, Dropout=False):
        super().__init__(input_channels, output_channels,
                        BN=BN, Dropout=Dropout)

        self.conv1 = nn.Sequential(
            nn.Conv2d(input_channels, output_channels, kernel_size=3, padding=1).to(globalParam.device),
            nn.BatchNorm2d(output_channels).to(globalParam.device),
            nn.ReLU()
        ) if self.BN == True else nn.Sequential(
            nn.Conv2d(input_channels, output_channels, kernel_size=3, padding=1).to(globalParam.device),
            nn.ReLU()
        )

        self.conv2 = nn.Sequential(
            nn.Conv2d(output_channels, output_channels, kernel_size=3, padding=1).to(globalParam.device),
            nn.BatchNorm2d(output_channels).to(globalParam.device)
        ) if self.BN == True else nn.Sequential(
            nn.Conv2d(input_channels, output_channels, kernel_size=3, padding=1).to(globalParam.device),
            nn.ReLU()
        )
        # 旁路卷积，卷积核为1，控制通道改变，只对输入各像素产生整体线性变化
        self.conv_side = nn.Conv2d(input_channels, output_channels, kernel_size=1).to(globalParam.device)

    def forward(self, x):
        y = self.conv1(x)
        y = self.conv2(y)
        if self.input_channels != self.output_channels:
            x = self.conv_side(x)
        return F.relu(x + y)


# 瓶颈模块
# 参数量：input*low+low*low*3*3+low*output+(input*output)
# 输出通道不为1，为1时考虑用residual block
class BottleneckBlock(BlockInterface):
    def __init__(self, input_channels, output_channels, 
                BN=True, Dropout=False):
        super().__init__(input_channels, output_channels,
                        BN=BN, Dropout=Dropout)
        low_channels = output_channels // 4  # 默认low_channels是output_channels的四分之一

        self.conv1 = nn.Sequential(
            nn.Conv2d(input_channels, low_channels, kernel_size=1).to(globalParam.device),
            nn.BatchNorm2d(low_channels).to(globalParam.device),
            nn.ReLU()
        ) if self.BN == True else nn.Sequential(
            nn.Conv2d(input_channels, low_channels, kernel_size=1).to(globalParam.device),
            nn.ReLU()
        )

        self.conv2 = nn.Sequential(
            nn.Conv2d(low_channels, low_channels, kernel_size=3, padding=1).to(globalParam.device),
            nn.BatchNorm2d(low_channels).to(globalParam.device),
            nn.ReLU()
        ) if self.BN == True else nn.Sequential(
            nn.Conv2d(low_channels, low_channels, kernel_size=3, padding=1).to(globalParam.device),
            nn.ReLU()
        )

        self.conv3 = nn.Sequential(
            nn.Conv2d(low_channels, output_channels, kernel_size=1).to(globalParam.device),
            nn.BatchNorm2d(output_channels).to(globalParam.device),
        ) if self.BN == True else nn.Sequential(
            nn.Conv2d(low_channels, output_channels, kernel_size=1).to(globalParam.device),
        )

        # 旁路卷积，卷积核为1，控制通道改变，只对输入各像素产生整体线性变化
        self.conv_side = nn.Conv2d(input_channels, output_channels, kernel_size=1).to(globalParam.device)

    def forward(self, x):
        y = self.conv1(x)
        y = self.conv2(y)
        y = self.conv3(y)
        if self.input_channels != self.output_channels:
            x = self.conv_side(x)
        return F.relu(x + y)

1.5 DenseNet, 2017

DenseNet（稠密连接网络）就是一种受到ResNet启发而设计的网络结构。其主题思想和ResNet一致的，但有两点区别：

  1. 跨层连接使用cat（通道叠加）而不是简单地相加
  2. 稠密连接，套娃连接…
  3. 由于使用cat增大了通道数，所以还得使用过渡层适当减小通道数。
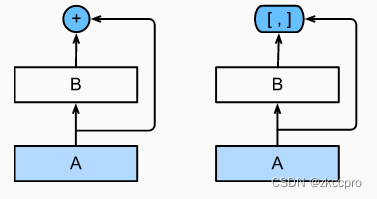
    请添加图片描述
    图7 稠密块的通道叠加

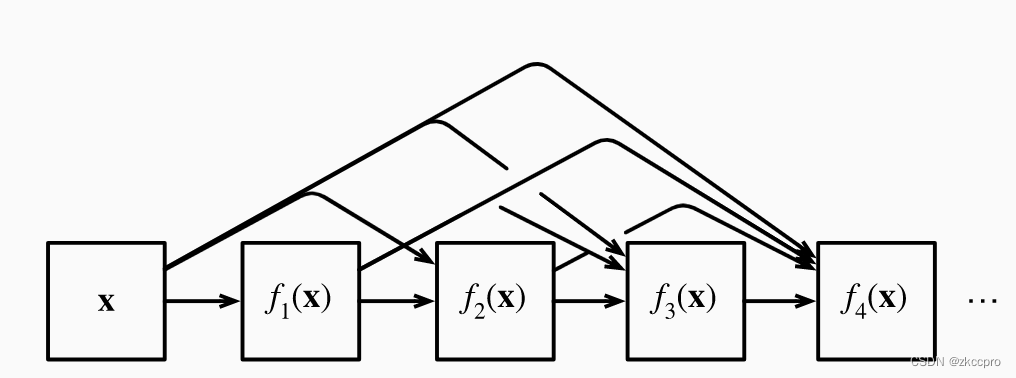
请添加图片描述
图8 稠密连接示意

附上稠密块、过渡块以及DesNet整体模型的pytorch实现：

import torch
from torch import nn


def conv_block(input_channels, num_channels):
    return nn.Sequential(
        nn.BatchNorm2d(input_channels), nn.ReLU(),
        nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1))

# 稠密块
class DenseBlock(nn.Module):
    def __init__(self, num_convs, input_channels, num_channels):
        super(DenseBlock, self).__init__()
        layer = []
        for i in range(num_convs):
            layer.append(conv_block(
                num_channels * i + input_channels, num_channels))
        self.net = nn.Sequential(*layer)

    def forward(self, X):
        for blk in self.net:
            Y = blk(X)
            # 连接通道维度上每个块的输入和输出
            X = torch.cat((X, Y), dim=1)
        return X


# 过渡层
def transition_block(input_channels, num_channels):
    return nn.Sequential(
        nn.BatchNorm2d(input_channels), nn.ReLU(),
        nn.Conv2d(input_channels, num_channels, kernel_size=1),
        nn.AvgPool2d(kernel_size=2, stride=2))


# DenseNet整体实现
# num_channels为当前的通道数
num_channels, growth_rate = 64, 32
num_convs_in_dense_blocks = [4, 4, 4, 4]
blks = []
for i, num_convs in enumerate(num_convs_in_dense_blocks):
    blks.append(DenseBlock(num_convs, num_channels, growth_rate))
    # 上一个稠密块的输出通道数
    num_channels += num_convs * growth_rate
    # 在稠密块之间添加一个转换层，使通道数量减半
    if i != len(num_convs_in_dense_blocks) - 1:
        blks.append(transition_block(num_channels, num_channels // 2))
        num_channels = num_channels // 2
densenet = nn.Sequential(
    b1, *blks,
    nn.BatchNorm2d(num_channels), nn.ReLU(),
    nn.AdaptiveAvgPool2d((1, 1)),
    nn.Flatten(),
    nn.Linear(num_channels, 10))

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/652020.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

10倍|中科院再传好消息：比英伟达还快，“新技术”实现弯道超车

10倍|中科院再传好消息：比英伟达还快，“新技术”实现弯道超车

中科院再传好消息：在光芯片上有了重大突破，李明-祝宁华团队研制出了一款超高集成度光学卷积处理器。 这种方案具有高算力密度、超高的线性扩展性！ 基于这种技术的，光芯片的性能将再次提升，光芯片是用于AI,如果能变成现…
阅读更多...
每日算法（第二十四期）

每日算法（第二十四期）

先来回顾一下上期的问题及答案： 2023年6月15日 「电话号码的字母组合」（Letter Combinations of a Phone Number）。以下是题目的描述： 给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。给出数字到字母的…
阅读更多...
记录--前端如何优雅导出多表头xlsx

记录--前端如何优雅导出多表头xlsx

这里给大家分享我在网上总结出来的一些知识，希望对大家有所帮助 前言 xlsx导出是比较前后端开发过程中都比较常见的一个功能。但传统的二维表格可能很难能满足我们对业务的需求，因为当数据的维度和层次比较多时,二维表格很难以清晰和压缩的方式展现所有的…
阅读更多...
macOS Ventura 13.5beta3（22G5048d）发布

macOS Ventura 13.5beta3（22G5048d）发布

系统介绍 黑果魏叔 6 月 16 日消息，苹果今日向 Mac 电脑用户推送了 macOS 13.5 开发者预览版 Beta 3 更新（内部版本号：22G5048d），本次更新距离上次发布隔了 15 天。 macOS Ventura 带来了台前调度、连续互通相机、Fa…
阅读更多...
【Axure 教程】中继器（进阶篇）

【Axure 教程】中继器（进阶篇）

一、修改、删除指定行 首先我们还是在 Axure 页面中拖入一个【中继器】，并双击打开，在默认的【矩形】后面加上【修改】和【删除】按钮： 然后我们给修改按钮添加【中继器事件】，选择【更新行】： 可以看到，由…
阅读更多...
Axure RP 9 基础教程 元件基础3

Axure RP 9 基础教程 元件基础3

11、组合元件 Axure中可以将多个元件组合起来，组合可以被命名，也可以被当成一个元件来进行交互，调整位置和大小等。选中多个元件，在顶部菜单中点击组合图标即可。选中一个组合，点击取消组合，可以就地解散。…
阅读更多...
多传感器融合分类及对比

多传感器融合分类及对比

1.多传感器融合的体系结构 在多传感器融合中，按照对原始数据处理方法的不同，多传感器融合系统的体系结构可以分为三种：集中式，分布式和混合式(混合式又分为有反馈结构和无反馈结构)。 集中式融合：将各传感器获得的原始…
阅读更多...
软件设计的核心方法及实例解析

软件设计的核心方法及实例解析

李连杰电影版《倚天屠龙记》里有个经典的名场面，祖师爷爷张三丰花了三分钟教张无忌太极拳，张无忌学成打败了对手。三丰爷爷的教学思路是这样的：爷爷演示太极拳让张无忌跟着练，边练边问张无忌记住了多少，等张无忌把所有…
阅读更多...
网络系统安全——MS15_034漏洞利用与安全加固

网络系统安全——MS15_034漏洞利用与安全加固

Kali 192.168.124.162 Windows server 2008 192.168.124.169 检查2008服务器的IIS网站是否正常，进入2008服务器，使用ie浏览器访问本机地址 切换到kali，使用命令ping来测试他们的连通性 然后使用使用命令curl测试，测试&#x…
阅读更多...
FTP协议，带你了解FTP协议

FTP协议，带你了解FTP协议

目录 一、FTP的概述 1.FTP的理念 2.FTP数据连接模式 3.连接模式分类 4.主动和被动模式的工作原理 二、配置FTP服务 1、配置匿名用户FTP服务 1. 1安装FTP服务器软件 1.2 配置FTP服务器 1.3 重启FTP服务器 1.4 测试FTP服务器 2.关闭防火墙安装vsftpd软件包 3.开启FTP…
阅读更多...
单片机中移植lua解释器

单片机中移植lua解释器

一、基本开发环境 开发环境基于野火STM32开发板。 前测试的 Lua 解释器版本为 5.4.2。 官网下载lua资源包，下载地址如下： https://www.lua.org/ https://github.com/rjpcomputing/luaforwindows/releases lua: Lua 国内镜像 (gitee.com)‍ 二、移植Lua解…
阅读更多...
AIGC数据库工具-阿里开源Chat2DB

AIGC数据库工具-阿里开源Chat2DB

前言 今天无意间发现了一个AIGC数据库工具，chat2DB，重点！！！阿里开源，其设计产品的思想给了我很多灵感，故记录一下，并分享给大家。 概述： Chat2DB 是一款有开源免费的多…
阅读更多...
驱动开发：内核RIP劫持实现DLL注入

驱动开发：内核RIP劫持实现DLL注入

本章将探索内核级DLL模块注入实现原理，DLL模块注入在应用层中通常会使用CreateRemoteThread直接开启远程线程执行即可，驱动级别的注入有多种实现原理，而其中最简单的一种实现方式则是通过劫持EIP的方式实现，其实现原理可总结为&am…
阅读更多...
【C++】入门基础知识详解（二）

【C++】入门基础知识详解（二）

目录 一、内联函数 1、概念 2、特性 3、内联函数与宏的优缺点 二、auto关键字(C11) 1、auto 简介 2、auto的使用细则 2.1 auto与指针和引用结合起来使用 2.2 在同一行定义多个变量 3、auto不能推导的场景 3.1 auto 不能作为函数的参数 3.2 auto 不能直接用来声明数组 三、…
阅读更多...
英语中如何描述五颜六色

英语中如何描述五颜六色

前言 如何用英语描述五颜六色，看完这篇文章，你就学会了 🏠个人主页：我是沐风晓月 🧑个人简介：大家好，我是沐风晓月，阿里云社区博客专家 😉😉 💕 …
阅读更多...
Axure RP 9 基础教程 元件基础2

Axure RP 9 基础教程 元件基础2

第一章：Axure RP 9的元件(2) 6、改变元件的位置 要改变元件的位置，只需要拖动对应的元件即可。另外也可以在顶部快捷样式菜单中设置坐标值，然后按回车键，让元件移动到指定位置。 X轴是横轴，改变可以调整左右的位置。 Y…
阅读更多...
技术科普与解读：ChatGPT 大模型硬核解读！（一）家族历史从GPT-1到ChatGPT

技术科普与解读：ChatGPT 大模型硬核解读！（一）家族历史从GPT-1到ChatGPT

多模态，指的是融合文本、图像、视频或音频等多种模态作为输入或输出。 GPT-4是严格意义上的多模态模型，可以支持图像和文字两类信息的同时输入，输出为文本。从学术界的分析来看，无论是知识/能力获取还是与现实物理世界的交互&…
阅读更多...
【应用安全架构】什么是联合身份管理？

【应用安全架构】什么是联合身份管理？

介绍 联合身份管理是一种可以在两个或多个信任域之间进行的安排，以允许这些域的用户使用相同的数字身份访问应用程序和服务。这称为联合身份，使用这种解决方案模式称为身份联合。 联合身份管理建立在两个或多个域之间的信任基础之上。例如，信…
阅读更多...
如此有艺术感的AI生成式二维码，你肯定没有见过

如此有艺术感的AI生成式二维码，你肯定没有见过

这是一张很常见的图片，要说有特殊的话可能是由 AI 来生成的，其它并无特别之处。但给它加上三个定位点后，这张图就变成一个可以扫描识别的二维码： 真的假的？不信你长按图片识别一下！我一次看到时&#xff0c…
阅读更多...
基于Hexo和Butterfly创建个人技术博客，(8) 博客网站butterfly主题UI框架美化

基于Hexo和Butterfly创建个人技术博客，(8) 博客网站butterfly主题UI框架美化

Butterfly官方网站，请 点击进入 说明： 此文中的设置并不影响网站的整体，只是一些视觉上的调整，可以按需调整。 本章目标： 掌握butterfly主题的配置，优化UI样式 一、特效 1、过场动画 在每个页面打开前会有…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023