先来回顾一下上期的问题及答案:
2023年6月15日
「电话号码的字母组合」(Letter Combinations of a Phone Number)。以下是题目的描述:
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
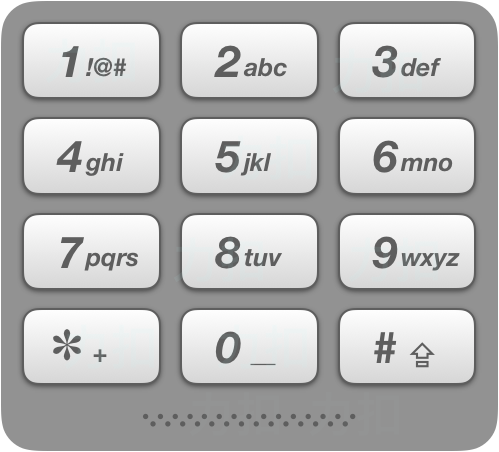
示例:
输入:"23"
输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]说明:
尽管上面的答案是按字典序排列的,但是你可以任意选择答案输出的顺序。
以下是对应的JavaScript解答:
const letterCombinations = function(digits) {
if (!digits || digits.length === 0) {
return [];
}
const mappings = {
"2": ["a", "b", "c"],
"3": ["d", "e", "f"],
"4": ["g", "h", "i"],
"5": ["j", "k", "l"],
"6": ["m", "n", "o"],
"7": ["p", "q", "r", "s"],
"8": ["t", "u", "v"],
"9": ["w", "x", "y", "z"]
};
const combinations = [];
const backtrack = (current, nextDigits) => {
if (nextDigits.length === 0) {
combinations.push(current);
return;
}
const letters = mappings[nextDigits[0]];
for (let i = 0; i < letters.length; i++) {
backtrack(current + letters[i], nextDigits.slice(1));
}
};
backtrack("", digits);
return combinations;
};解题思路:
使用回溯法来构建所有可能的字母组合。
定义一个映射
mappings,将数字和对应的字母数组进行关联。初始化一个空数组
combinations,用于存储所有的字母组合。编写回溯函数
backtrack,该函数接受两个参数:当前已经组合的字母字符串current和剩余的数字字符串nextDigits。当剩余数字字符串的长度为 0 时,说明已经遍历完所有的数字,将当前组合的字母字符串加入
combinations数组中。如果剩余数字字符串的长度不为 0,则获取剩余数字字符串的第一个数字对应的字母数组。
遍历该字母数组的每个字母,将当前字母与剩余数字字符串的子串进行递归调用
backtrack。最终返回
combinations数组,即所有可能的字母组合。
时间复杂度分析:
假设输入的数字字符串的长度为 n,最坏情况下每个数字对应的字母有 4
个,那么总共会有 4^n 个字母组合。
构建所有字母组合的时间复杂度为 O(4^n)。
空间复杂度分析:
使用了常数级别的额外空间来存储字母组合结果和映射关系,不考虑输出结果的空间占用。
空间复杂度为 O(1)。
2023年6月16日
「四数之和」(4Sum)。
题目描述:
给定一个包含 n 个整数的数组 nums 和一个目标值 target,判断 nums 中是否存在四个元素 a、b、c 和 d,使得 a + b + c + d 的值与 target 相等?找出所有满足条件且不重复的四元组。
注意:
答案中不可以包含重复的四元组。
示例:
输入:nums = [1,0,-1,0,-2,2],target = 0输出:[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]
提示:
可以使用双指针法来解决。可以固定两个数,然后使用双指针在剩余的部分进行查找。
需要注意的是,由于题目要求不可以包含重复的四元组,所以在查找过程中要注意去重。
上面问题的答案会在第二天的公众号推文中公布,大家可以关注公众号:程序员每日三问,第一时间获得推送内容。
学习不打烊,充电加油只为遇到更好的自己,每天早上9点纯手工发布面试题(死磕自己,愉悦大家) 希望大家在这浮夸的程序员圈里保持冷静,每天坚持花20分钟来学习与思考,在千变万化,类库层出不穷的今天,不要等到找工作时才狂刷题,提倡每日学习。