又是鸽了三千万年

马上要打csp了，开始回流学j组的知识了，浅说一下二分吧（）

---------------------------------------------------------------------------------------------------------------------------------

二分查找

二分查找，是一种极其高效的算法。它适用于在一个有序数组中找一个元素。注意：一定是有序，无序数组的查找答案是无意义的

假设在一个升序数组里寻找一个数字，定义一个区间，两个变量，表示区间的起始和终止坐标。每次去寻找这个区间内的中间值，分为三种可能性：

（1）这个数就是要找的，那么结束搜索。

（2）这个数比要找的小，那么改变区间的起始坐标，将区间整体右移。

 

 

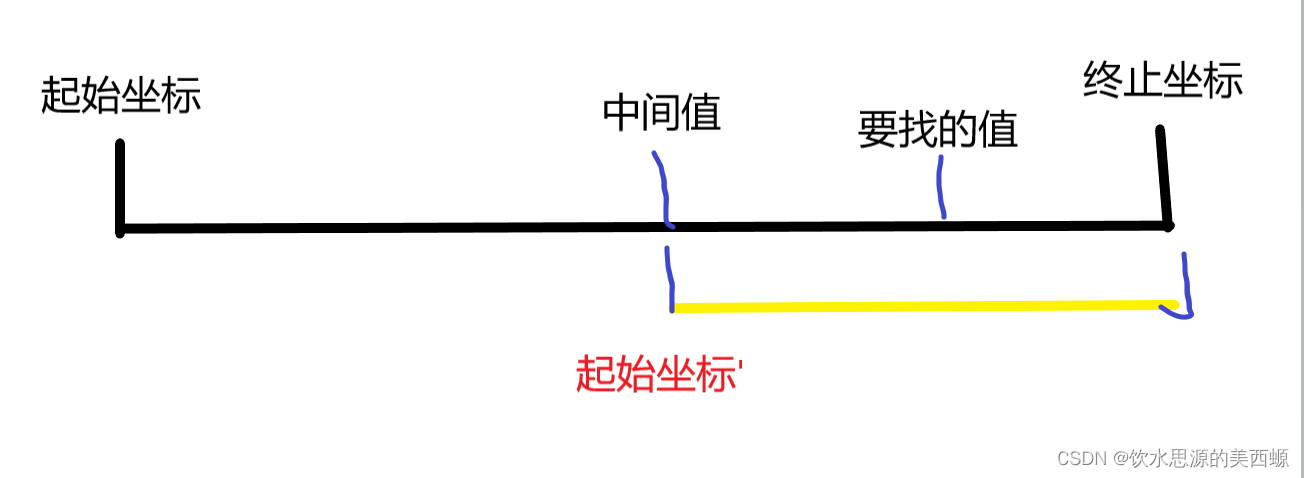
（3）这个数比要找的大，那么改变区间的终止坐标，将区间整体左移。

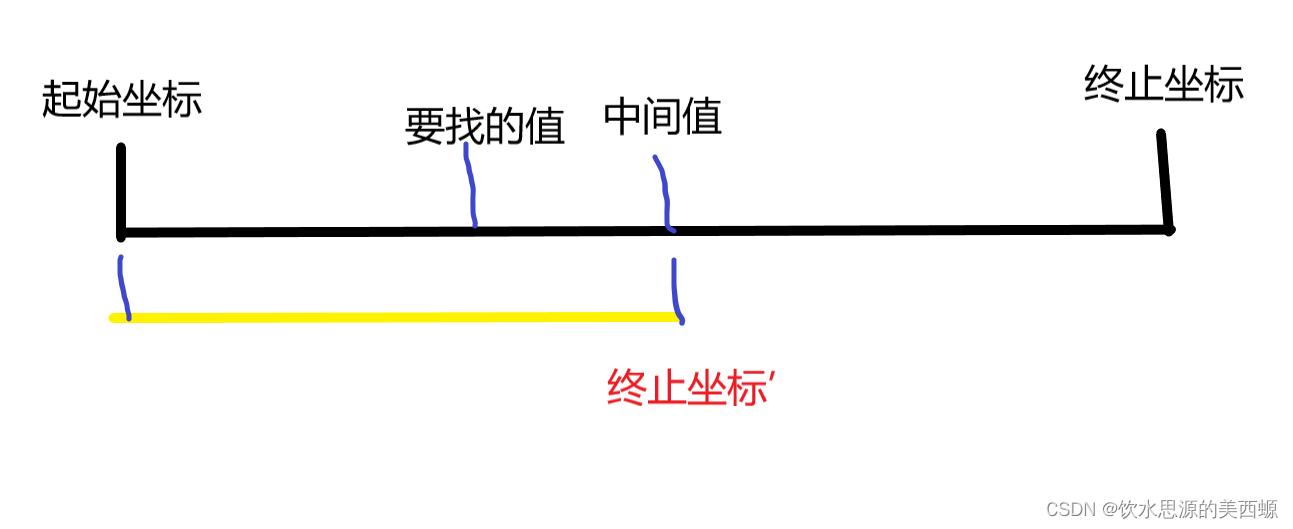
那么我们定义一个循环，且区间的起始坐标默认为1，终止坐标默认为n，只要起始坐标小于等于终止坐标（意思是说，这个区间还存在）循环中每次去取这个区间的中间坐标，再按照刚才的步骤去对比，不断调整，直到跳出循环。

以上是升序数组的方法，降序则相反

核心代码：

其中left,right代表区间起始终止坐标，a代表原数组值，mid代表每次取的中间值

 在STL中，给出了三个有关二分查找的函数：upper_bound,lower_bound,binary_search，这三个函数使用前都需引用<algorithm>

1.upper_bound:返回序列中第一个大于等于此元素的值。运用形式：upper_bound(a,a+1+n,x)，其中a与代码中的意思一样，都是目标数组，x为此元素。

2.lower_bound:返回序列中第一个大于此元素的值。运用形式：lower_bound(a,a+1+n,x)，其中a与代码中的意思一样，都是目标数组，x为此元素。

3.binary_search:二分模版，输入一个元素，输出位置。binary_search(a,a+1+n,x)，其中a与代码中的意思一样，都是目标数组，x为此元素。

需要注意的是：以上三个函数如果在序列中找不到目标元素（即大于目前元素或大于等于目前元素），那么就会返回a+1+n，是无效值。

以上三个函数默认是对升序数组进行排序，如果想要更改排序准则，需自写函数。如果想要对降序数组排序，可以这样：

先自写一个cmp排序数组

然后在函数的最后加上cmp，如：upper_bound(a,a+1+n,x,cmp)

二分查找例题： 

题目描述

输入 n 个不超过 10^9 的单调不减的（就是后面的数字不小于前面的数字）非负整数 a1​,a2​……，an​，然后进行 m 次询问。对于每次询问，给出一个整数 q，要求输出这个数字在序列中第一次出现的编号，如果没有找到的话输出 −1 。

输入格式

第一行 2 个整数n 和 m，表示数字个数和询问次数。

第二行 n 个整数，表示这些待查询的数字。

第三行 m 个整数，表示询问这些数字的编号，从 1开始编号。

输出格式

输出一行，m 个整数，以空格隔开，表示答案。

输入 #1
11 3
1 3 3 3 5 7 9 11 13 15 15
1 3 6
输出 #1
1 2 -1 

 题目中明确说“单调不减”，很明显的提示了不降序数列，直接套一下二分查找模版即可。

这道题就留给大家了，在这里不过多讲解了~

分析优劣性：

优点：高效，省时省力，算下来只有O(log n)的时间复杂度

缺点：不同的题目在判断情况时容易混淆“<"和“<="或者“>"和">="。

---------------------------------------------------------------------------------------------------------------------------------

今天对于二分查找的讲解就到这里，大家有问题随时评论区提问~~