目录

1，概念

2，数学知识

3，前提条件

4，序列不平稳时的平稳性方法

5，模型定阶，确定P和Q

6，模型训练与检验

---

1，概念

        ARIMA模型（英语：Autoregressive Integrated Moving Average model），差分整合移动平均自回归模型，ARIMA(p，d，q)中，AR是自回归，p为自回归项数；MA为滑动平均，q为滑动平均项数，d为使之成为平稳序列所做的差分次数（阶数）。“差分”一词虽未出现在ARIMA的英文名称中，却是关键步骤。

        大致思路就是：1，当前时刻点的取值与之前相邻一个或者多个时刻点自相关，并假设他们满足一个线性关系。2，由于每一个时刻点采集的数据都存在服从一定分布的误差，且当前时刻不仅由自己的采集误差，也与之前一个或者多个时刻的误差相关，并假设他们满足一个线性关系。3，将这两部分结合在一起就是ARIMA模型。

2，数学知识

        假设检验时如何设置原假设和备选假设。一般原假设都不是我们所期望的情况，我们的目的就是去寻找证据推翻原假设，即拒绝原假设接受备选假设，备选假设就是我们所想要的情况。

        原因是：犯第二类错误也叫取假错误，把错的当真的，这是万万不可的。犯第一类错误时，我们还有一个显著性水平α来限制我们犯错，这是可以接受的，俗称赌一把。如果证据不足，无法推翻原假设，这时我们不得不接受原假设，就完全避免了犯第二类错误的情况。如证据充足，我们能够推翻原假设，接受了备选假设，此时我们犯错的概率小于显著性水平α，但是α很小，即我们犯错的可能性很低。

3，前提条件

        ARIMA模型只能对平稳序列进行分析，无法对非平稳序列进行分析。所以拿到一个时间序列之后，首先需要进行平稳性检验和白噪声检验。

• 白噪声检验

        白噪声是指序列是纯随机数据，纯随机游走，是无意义的数据，继续研究毫无意义，比如使用random生成的服从正态分布的一串时间序列就属于白噪声。白噪声检验也称为纯随机性检验，当数据是纯随机数据时，再对数据进行分析就没有任何意义了。常使用acorr_ljungbox函数对序列进行白噪声检验。

from statsmodels.stats.diagnostic import acorr_ljungbox  # 随机性检验库
# 数据的纯随机性检验函数
acorr_ljungbox(data)

        acorr_ljungbox的原理：原假设H0：是白噪声；备选假设H1：是非白噪声。他构造了卡方统计量，显著性水平为0.5。且使用p_value这个更强的证据来做证明，当p远小于α显著性水平时我们拒绝原假设接受备选假设，当p值大于0.5时，证据不足，无法推翻原假设，序列就是白噪声。

• 平稳性检验

        平稳性就是指记录的某个特征变量如果满足正态分布U(0,1),那么在任意时刻记录的值都服从Z(0,1)，而不是Z(0,2)。一般使用ADF单位根进行平稳性检验。

        ADF是假设检验的应用。H0原假设：是序列不平稳，即存在单位根；H1备选假设：是序列平稳，不存在单位根。我们需要做的就是找证据来推翻原假设，如果证据不足无法推翻我们就能够避免用ARIMA去分析序列这种错误做法。而且我们设置了显著性水平α，如果我们找到了证据推翻了原假设，我们犯错的概率(第一类的弃真错误)也是很小的。

        判断依据：ADF检验设计了一个ADF统计量，具体服从什么分布不清楚，一般默认t分布(用样本标准差代替总体方差)或者z分布。他是双侧检验，给定显著性水平之后，我们就能够知道拒绝域了，拒绝域的横坐标对应着相应的统计量计算值，只要计算出的ADF统计量在指定横坐标外侧我们就能够拒绝原假设，接受备选假设，即我们找到了证据证明序列不是不平稳的。  

        p值是比统计量更强的证据，假如统计量服从正态(0,1)分布，且拒绝域的横坐标是-2.56和2.56，但是我们计算出来的ADF统计量是3，那么p值就是X>3的概率值。其值越小越好，小于显著性水平α即可认为原假设不对，接受备选假设，即序列非平稳。

from statsmodels.tsa.stattools import adfuller

result = adfuller(data)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[4].items():
    print('\t%s: %.3f' % (key, value))

2.平稳性检验的一些其他方法

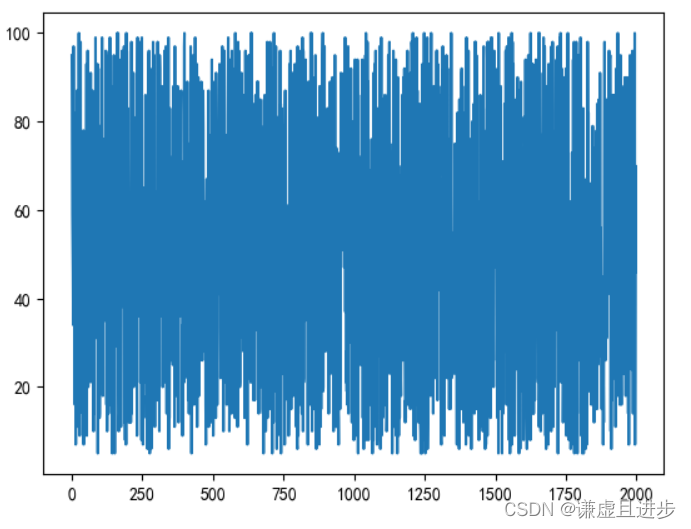
• 将数据使用plt画出来，用眼睛看，如果趋势变化明显，随着时间前进波动幅度变大，一般都是非平稳。下面这种随着时间前进，最大值和最小值的距离越来越多，肯定非平稳。

• 使用ACF图和PACF图进行眼睛看，如果没有出现截尾或者拖尾，那肯定是非平稳。

4，序列不平稳时的平稳性方法

        经过检验序列非平稳，可以使用差分让数据变为平稳，一般只进行一阶差分，如果一阶差分序列还是非平稳序列，那么最好的做法是：赶紧换个模型(比如LSTM等神经网络模型)，别死磕ARIMA。

        得到一阶差分之后，我们同样对一阶差分序列进行白噪声检验和平稳性检验，和对原序列的方法一致。一般一阶差分之后都会平稳，如果不平稳赶紧换模型。一般平稳序列的图如下所示：这种围绕某个值上下波动的情况都可以认为是平稳序列了。当然最直接的还是ADF检验。

5，模型定阶，确定P和Q

        如果原序列就是平稳的，定阶就使用原序列数据；如果进行了一阶差分变成了平稳序列，那么就使用一阶差分序列进行定阶。

        方法1：根据平稳序列的PACF定P，ACF定Q

        PACF的后截尾阶数就是P；ACF的后截尾阶数就是Q。PACF图中，最左边的相关系数是1，原因是自己跟自己的相关性当然是1。然后与其前1个、2个时刻的系数分别是-0.25左右，但是前第7个时刻由存在0.25左右的相关性。蓝色区域表示他们虽然存在相关性，但是可以忽略不计。

        ACF图也类似，说明存在一定的周期相关性。

        方法2：暴力求解法

        上面的方法过于无语，做了也是白做。下面介绍一种万无一失的方法，AIC和BIC定阶方法。由于我们已经得到了d的取值，要么0要么1。即P、Q、d我们知道了d，那么直接暴力遍历P、Q的取值，看一下那种组合下的AIC和BIC取值最小，我们就用那种组合。

import statsmodels.api as sma

# AR最大阶不超过6，MA最大阶不超过4。
aic_res= sma.tsa.arma_order_select_ic(diff1,max_ar=6,max_ma=4,ic=['aic']) # AIC
print('AIC', aic_res['aic_min_order'])

bic_res = sma.tsa.arma_order_select_ic(diff1,max_ar=6,max_ma=4,ic=['bic']) # BIC
print('BIC', bic_res['bic_min_order'] )

6，模型训练与检验

        通过上述过程，确定P、Q、d之后就可以拿数据拟合模型了，注意：如果进行了差分拟合数据得是差分数据才行。

        模型的残差检验：

        模型残差检验是想弄清楚模型是否完全的将数据特征提取完毕。可以这么认为：模型残差是白噪声，我们就认为序列特征已经被提取完毕。

modelf = sma.tsa.ARIMA(diff, order=(3, 4, 1))  # 传入参数，构建并拟合模型
result = modelf.fit()

# Ljung-Box检验
xx = acorr_ljungbox(result.resid, lags=10)
print(xx)

        上面就是使用arima模型的一般步骤。