回溯思想:


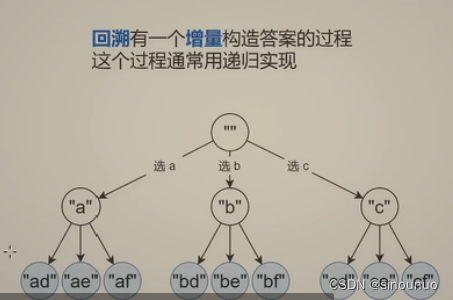

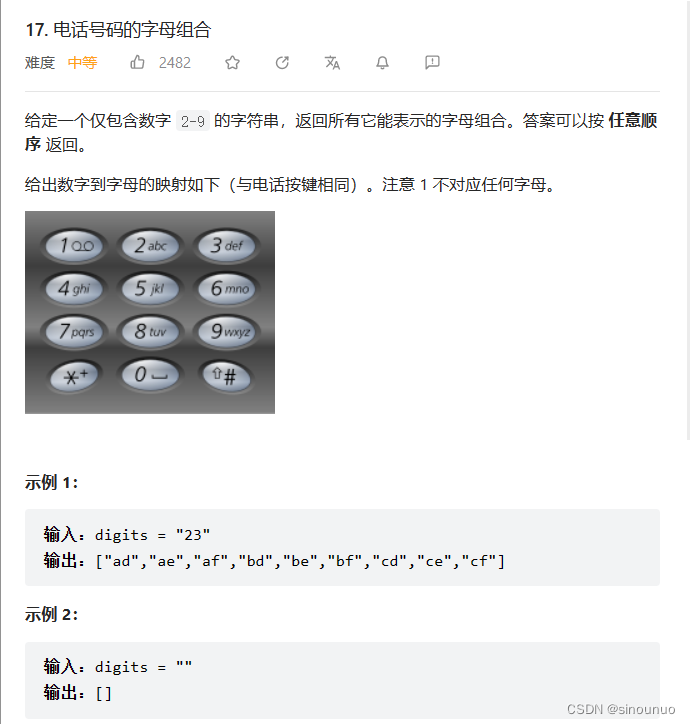
思路:这种出现全部xx组合的,基本都是回溯算法。首先,当digits是空,那返回也是空。当回溯到边界条件的时候,就更新答案,在非边界条件的时候,循环该数值下的全部情况。
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
dict_letter = {'2':['a','b','c'],
'3':['d','e','f'],
'4':['g','h','i'],
'5':['j','k','l'],
'6':['m','n','o'],
'7':['p','q','r','s'],
'8':['t','u','v'],
'9':['w','x','y','z']}
if len(digits) == 0:
return []
ans = []
def letter(path,num): #将每次的新组合传递下去
if len(num) == 0: #何时停止递,更新答案?
ans.append(path)
return
for c in dict_letter[num[0]]: #循环的子问题
letter(path+c,num[1:])
letter('',digits)
return ans

子集型回溯:

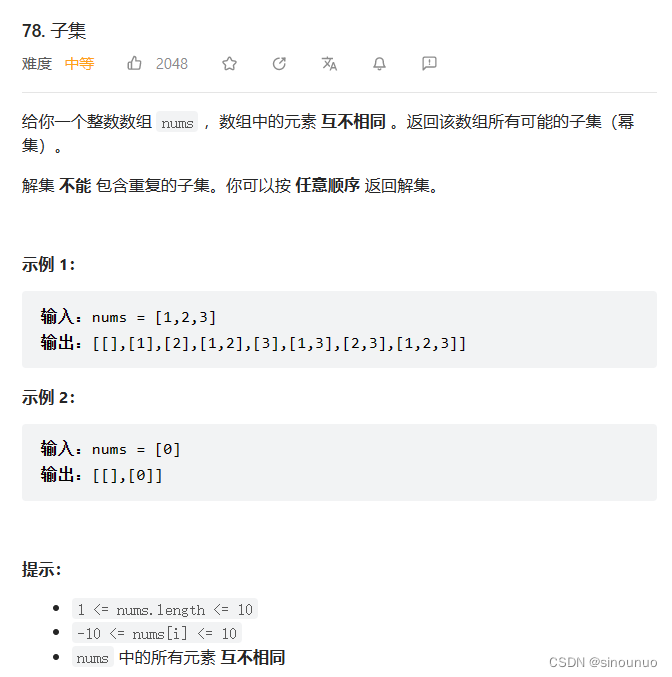
思路:对于nums中的每一个数字,都有选和不选两种可能,一共有n次选择的机会,用n来控制递归,每选择一次,就给n减一再去递归,直到n是0,就要将path写入答案。注意path是全局变量,要用copy固定答案,以及某一次选择子集之后,要恢复现场。(退回到根节点)
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
ans = []
path = []
n = len(nums)
def sets(n):
if n == 0:
ans.append(path.copy())#固定答案
return
sets(n-1) #不选该子集,直接递归
path.append(nums[n-1]) #选该子集
sets(n-1) #选该子集
path.pop() #恢复现场
sets(n)
return ans
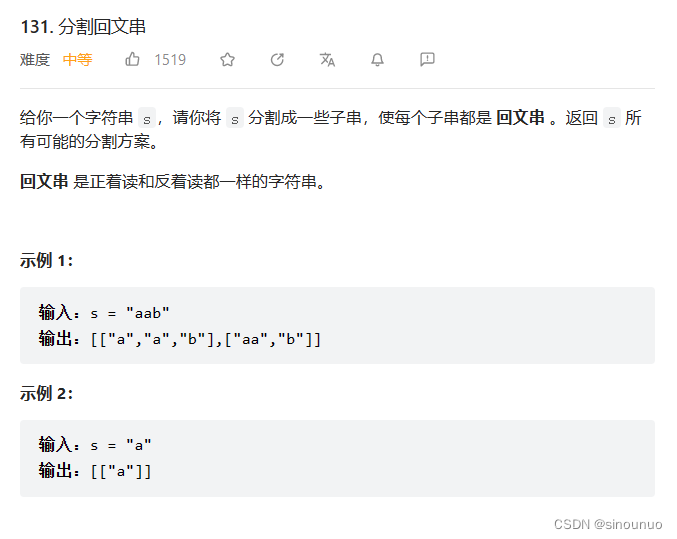
思路一:遍历子串的结束位置,对于每一个传入的i,遍历子串的结束位置,如果是回文串,就加入path中,然后继续递归之后的子串。
class Solution:
def partition(self, s: str) -> List[List[str]]:
ans = []
path = []
n = len(s)
def part(i): #子串的开始位置
if i == n:
ans.append(path.copy())
return
for j in range(i,n):#遍历子串的结束位置
t = s[i:j+1]
if t == t[::-1]: #是回文串
path.append(t)
part(j+1) #递归剩下的子串
path.pop()#恢复现场
part(0)
return ans
思路二:假设每个字母之间存在一个逗号,每次遇到逗号都要选择或者不选择。当不选择逗号时,初始位置start不变,但是终止位置i+1(i截止到n-1),当选择逗号时,意味着从逗号处开始分割,取此时的s[start:i+1],判断是否是回文串,如果是,就加入到path中,继续递归剩下的字符串(s[i+1:],开始位置和结束位置都重新设置为i+1),递归之后要恢复现场。
class Solution:
def partition(self, s: str) -> List[List[str]]:
ans = []
path = []
n = len(s)
def part(start,i): #子串的开始位置,结束的位置
if i == n:
ans.append(path.copy())
return
#不选择逗号
if i < n-1:
part(start,i+1) #只增加结束位置
#选择逗号
t = s[start:i+1] #取当前分割的字符串
if t == t[::-1]: #是回文串
path.append(t)
part(i+1,i+1) #递归剩下的子串
path.pop()#恢复现场
part(0,0)
return ans
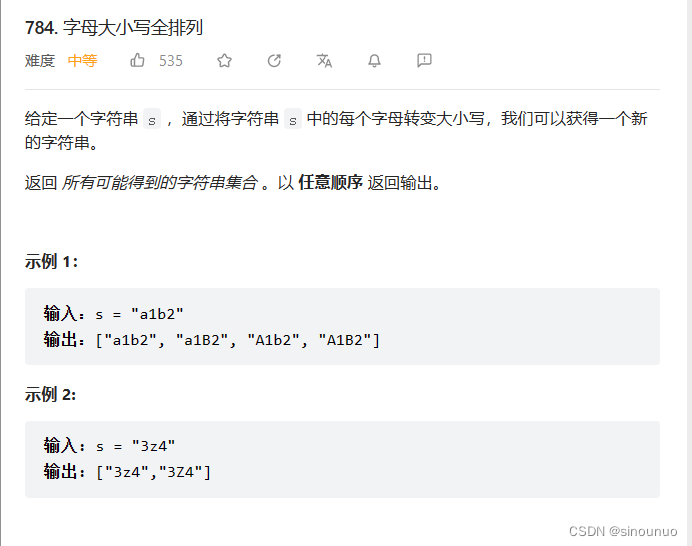
思路一:对于每个s[i]选择反转或者选择不反转
class Solution:
def letterCasePermutation(self, s: str) -> List[str]:
ans = []
n = len(s)
def bfs(i,path): #将层数和路径一起传递下去
if i == n:
ans.append(path)
return
#选择不反转
bfs(i+1,path+s[i])
#选择反转
if 'a' <= s[i] <= 'z' or 'A' <= s[i] <= 'Z':
bfs(i+1,path+s[i].swapcase())
bfs(0,'')
return ans
思路二:枚举s[i]判断是否是字母并修改,由于没有包含不修改选项,所以递归入口处就要把答案写进去,然后对剩下的字符串修改。
class Solution:
def letterCasePermutation(self, s: str) -> List[str]:
ans = []
n = len(s)
path = list(s)
def bfs(i):
ans.append(''.join(path)) #先写入答案
if i == n:
return
for j in range(i,n):#枚举下标并修改
if 'a' <= s[j] <= 'z' or 'A' <= s[j] <= 'Z':
path[j] = path[j].swapcase() #修改
bfs(j+1) #递归
path[j] = path[j].swapcase() #恢复现场
bfs(0)
return ans

思路:按照由简单到复杂的顺序来思考这个题:我们需要一个path来存储满足累加序列的list或者是只有两个元素的list。首先我们假设path不需要任何限制条件,就是找num的全部分割子集(代码中的橘色部分),然后我们需要考虑到,如果一个数首位是0,就不符合分割,加一个限制条件。然后我们path中要求满足累加,把path分成两种情况,第一种是有了两个元素了,就要判断是否满足累加,满足就加到path中。另一种情况是不足两个元素,那就直接加到path中,不需要判断。最后在递归的边界条件,要判断一下,path是否是大于两个元素,大于才能放入ans中。
class Solution:
def isAdditiveNumber(self, num: str) -> bool:
ans = []
path = []
n = len(num)
if n < 3:
return False
def dfs(i):
if i == n:
if len(path) >= 3: #长度大于2才能放入ans
ans.append(path.copy())
return
for j in range(i, n):
t = num[i:j+1]
if len(t) > 1 and t[0] == '0': #不符合分割的限制条件
continue
if len(path) >= 2:
if path[-1] + path[-2] == int(t): #是否满足累加
path.append(int(t))
dfs(j+1)
path.pop()
if len(path) < 2: #直接加到path中,不需要判断
path.append(int(t))
dfs(j+1)
path.pop()
dfs(0)
return len(ans) > 0

思路:对于[1,n]中的数字,每一个我们都要判断一下是否是符合

设置一个函数sumi,如果函数返回true,就符合,那就将其平方和加入答案中。sumi中先分割i*i的十进制,在边界条件中判断path和是否是i,是就加入ans,最后输出len(ans) > 0.。
class Solution:
def sumi(self,i):
power2 = str(i*i)
ans = []
path = []
n = len(power2)
def dfs(a):
nonlocal i
if a == n:
if sum(path) == i:
ans.append(path.copy())
return
for j in range(a,n):
t = power2[a:j+1]
path.append(int(t))
dfs(j+1)
path.pop()
dfs(0)
return len(ans) > 0
def punishmentNumber(self, n: int) -> int:
ans = 0
for i in range(1,n+1):
if self.sumi(i):
ans += i*i
return ans
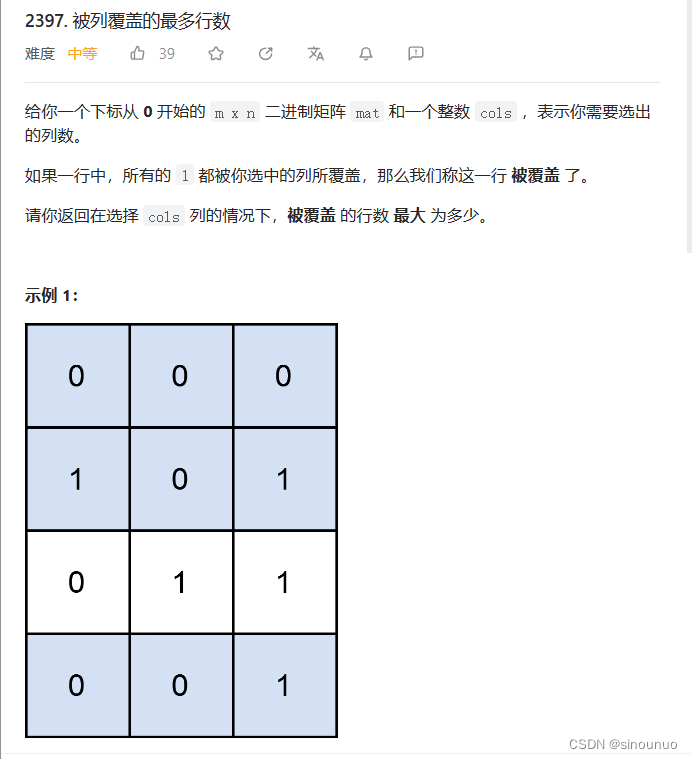
思路:将问题拆分开,我们首先计算出[0,len(mat[0])](一共多少列)有多少种可能的不重复的子集 (橘色),这些子集中,我们需要的path长度是cols,当长度符合时,去更新答案。对于任何一个确定的子集,计算行的和是否等于被覆盖的数的和,是则更新答案。
class Solution:
def rows(self,path,matrix):
ans = 0
for i in matrix:
sumj = 0
for j in path:
sumj += i[j] #被覆盖的数的和
if sum(i) == sumj: #行和是否等于被覆盖的数和
ans += 1 #被覆盖的行数
return ans
def maximumRows(self, matrix, numSelect: int) -> int:
res = -1
path = []
nums = [i for i in range(len(matrix[0]))] #求nums的可能子集
def dfs(i):
nonlocal res,path,nums
if i == len(nums):
if len(path) == numSelect: #当子集长度符合时,更新答案
res = max(self.rows(path.copy(),matrix),res)
return
dfs(i+1) #选
path.append(i) #不选
dfs(i+1)
path.pop()
dfs(0)
return res