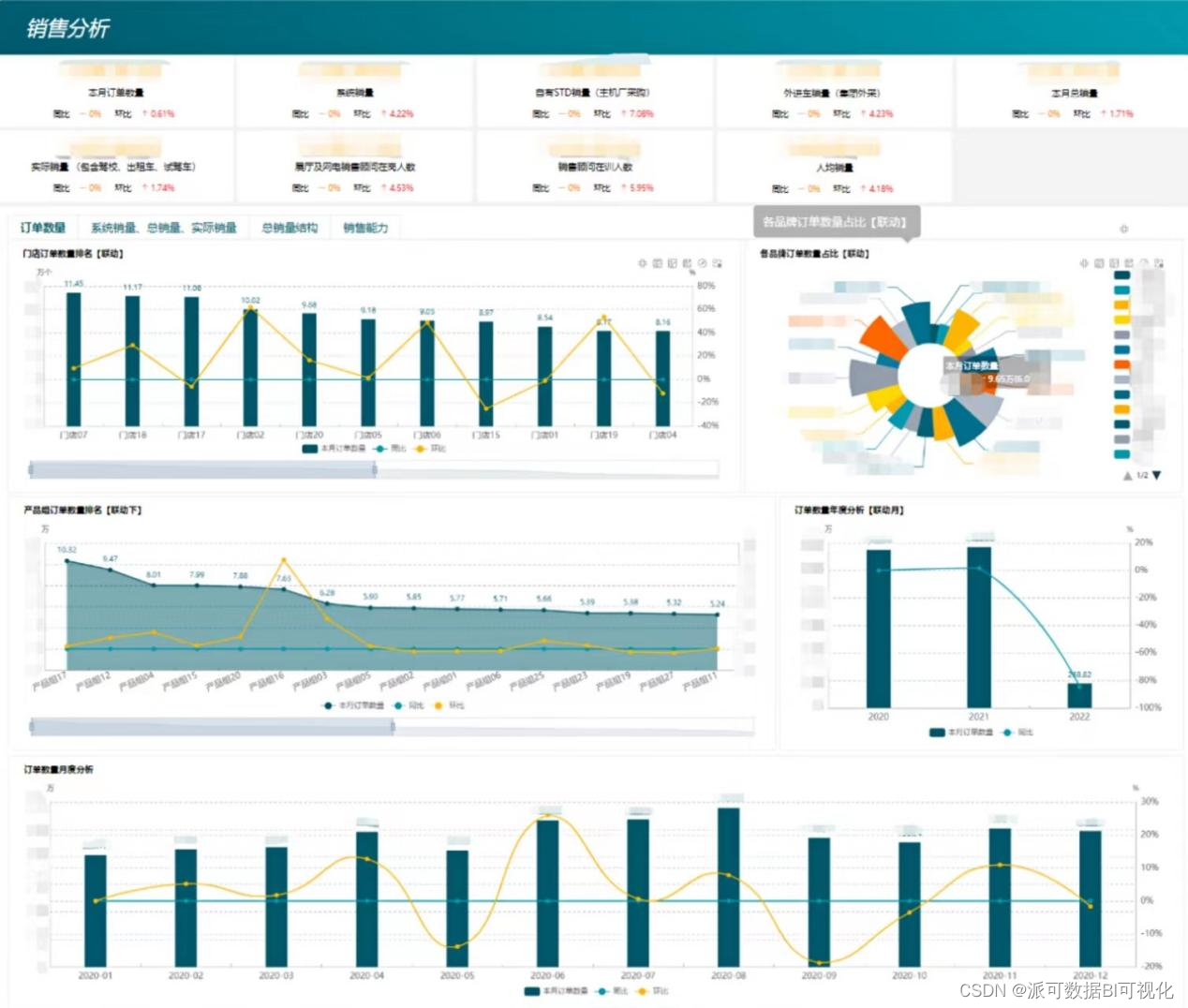
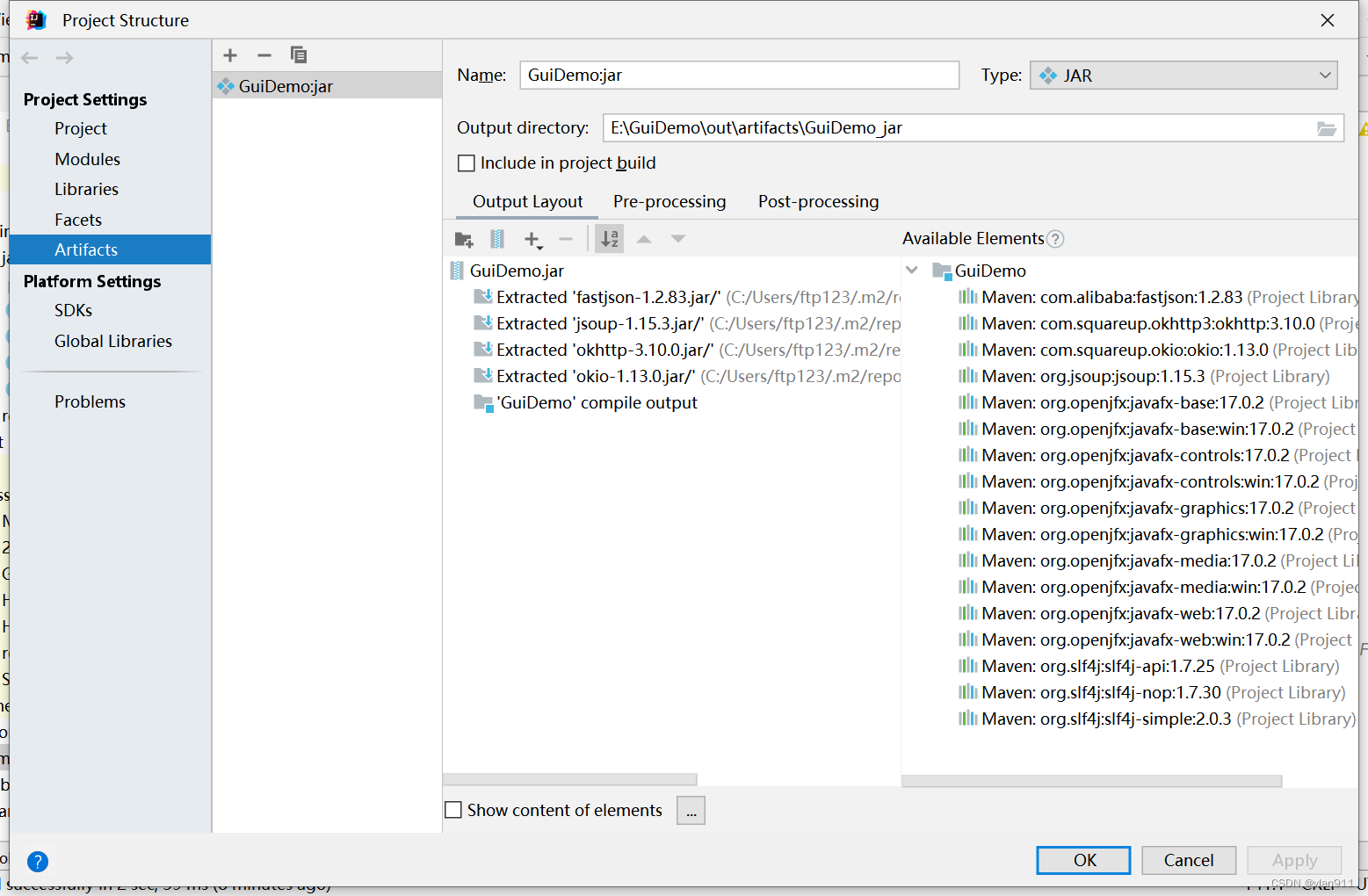
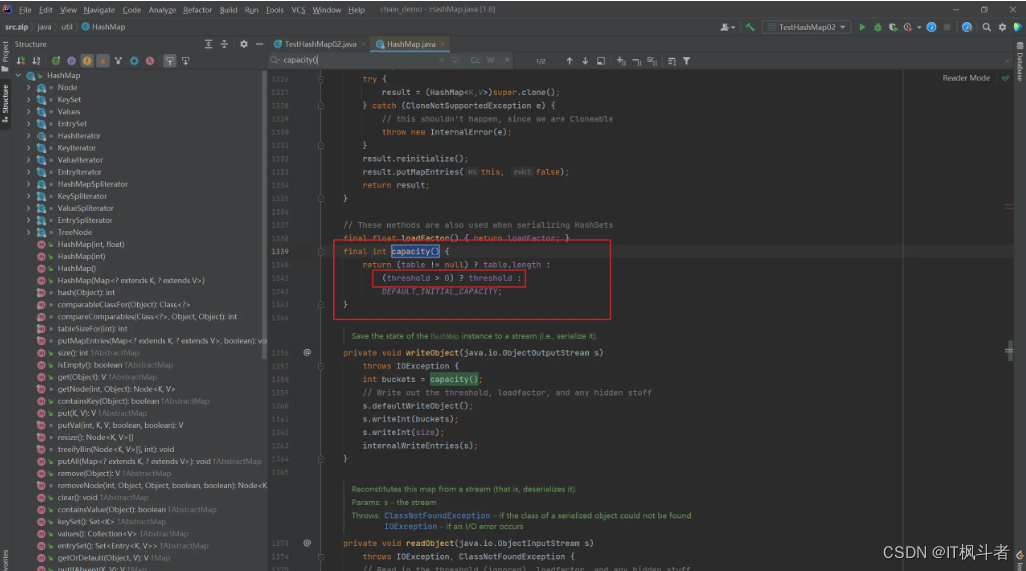
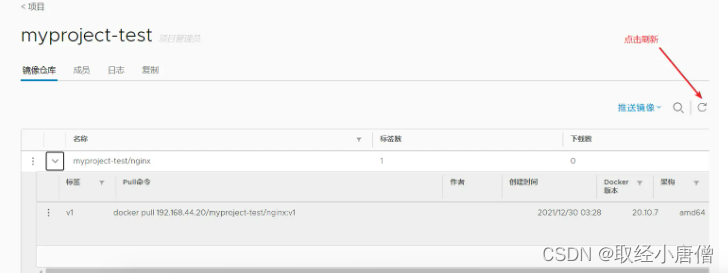
贝叶斯隐马尔可夫模型是一种用于分割连续多变量数据的概率模型。该模型将数据解释为一系列隐藏状态生成。每个状态都是重尾分布的有限混合,具有特定于状态的混合比例和共享的位置/分散参数。
相关视频:马尔可夫链原理可视化解释与R语言区制转换Markov regime switching实例
马尔可夫链原理可视化解释与R语言区制转换Markov regime switching实例
,时长07:25
相关视频
马尔可夫链蒙特卡罗方法MCMC原理与R语言实现
,时长08:47
该模型中的所有参数都配备有共轭先验分布,并通过变化的贝叶斯(vB)推理算法学习,其本质上与期望最大化相似。该算法对异常值具有鲁棒性,并且可以接受缺失值。
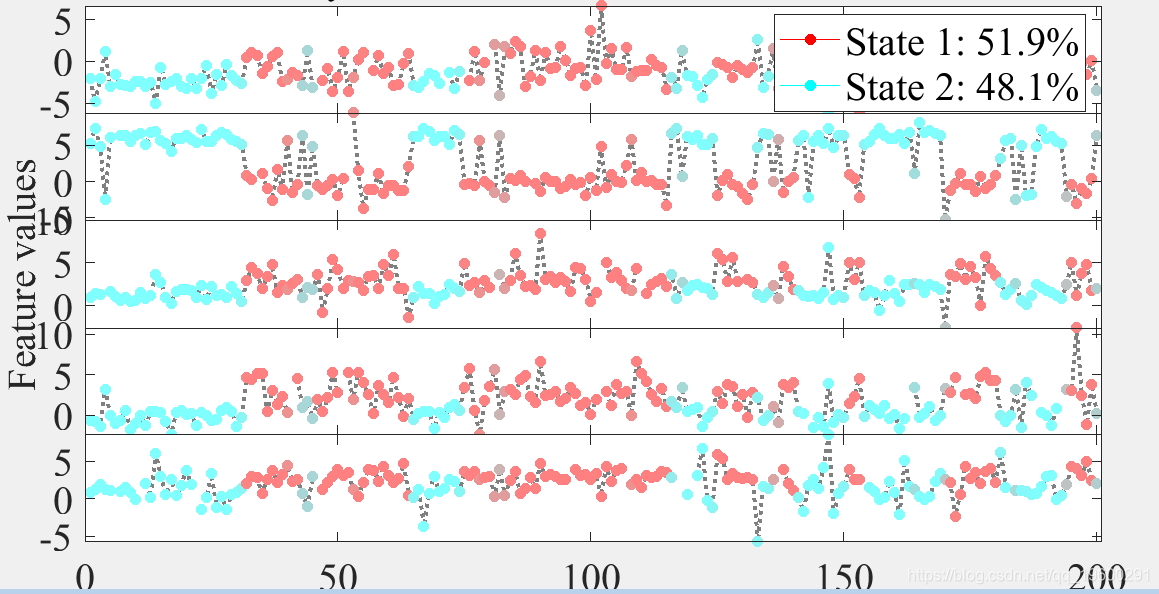
去年,我们为一家公司进行了短暂的咨询工作,该公司正在构建一个主要基于贝叶斯隐马尔可夫hmm的分析应用程序。本文从未知的BRHMM生成一组数据序列 参数,并仅从这些数据中估算出 生成它们的模型。 结果绘制为 时间序列
设置状态,符号和特征的数量
NumState=2;
NumSym=3;
NumFeat=5;设置序列数,每个序列点数和缺失值
NumSeq=2;
NumPoint=100;
NumMiss=20;设置参数生成选项。TransParam=1/5
EmissParam=1/5;
LocParam=2;
DispParam=5;设置采样选项
NumDeg=5;
NumObs=1000;打印 和显示状态
fprintf('\n')
fprintf('Sampling data ... ')生成用于采样的参数
[Trans,Emiss,Loc,Disp]=GenParam(NumState,NumSym,NumFeat,...
TransParam,EmissParam,LocParam,DispParam);

创建用于采样的模型
Obj= bhnn(NumState,NumSym,NumFeat);
设置超参数
Obj.TransWeight=Trans;
Obj.TransStren(:)=NumObs;
Obj.EmissWeight=Emiss;
Obj.EmissStren(:)=NumObs;
Obj.CompLoc=Loc;
Obj.CompScale(:)=NumObs;
Obj.CompDisp=Disp;
Obj.CompPrec(:)=max(NumObs,NumFeat);采样数据并随机删除值
更新状态
fprintf('Done\n')
fprintf('Estimating model ... ')创建估计模型
Obj=BHMM(NumState,NumSym,NumFeat);
约束过渡参数
Obj.TransWeight=Trans;
Obj.TransStren(:)=NumObs;估计模型和状态概率
更新状态

绘制结果

% 更新状态
fprintf('Done\n')
fprintf('\n')
end 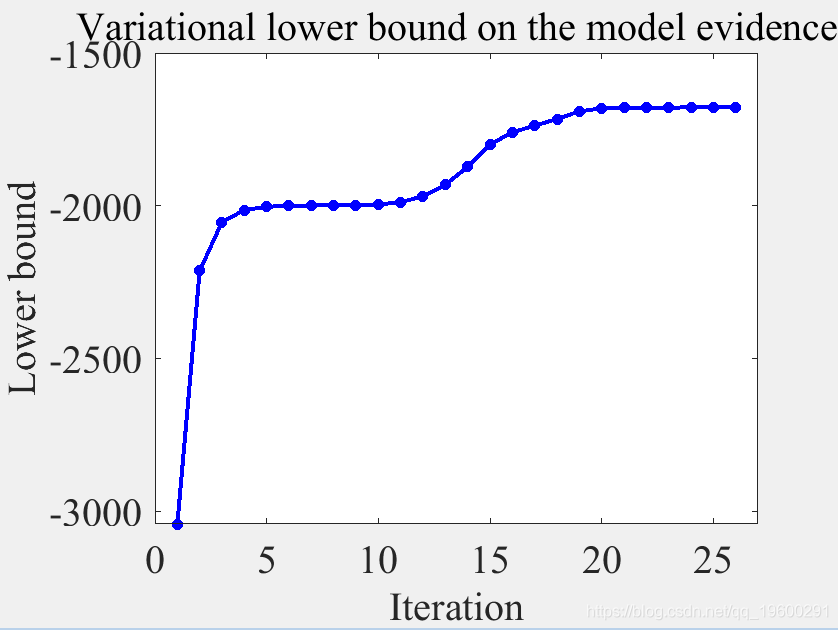



![[附源码]计算机毕业设计基于vuejs的文创产品销售平台app](https://img-blog.csdnimg.cn/dc78f1bb02974fa2bec3229d742fd92a.png)
![[附源码]计算机毕业设计甜品购物网站Springboot程序](https://img-blog.csdnimg.cn/6147589df72c4c79bfbd3358715dfbf3.png)