给你一个 m x n 的矩阵，其中的值均为非负整数，代表二维高度图每个单元的高度，请计算图中形状最多能接多少体积的雨水。

示例 1:

输入: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
输出: 4
解释: 下雨后，雨水将会被上图蓝色的方块中。总的接雨水量为1+2+1=4。

示例 2:

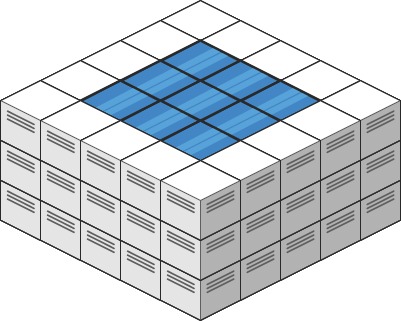
输入: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
输出: 10

提示:

• m == heightMap.length
• n == heightMap[i].length
• 1 <= m, n <= 200
• 0 <= heightMap[i][j] <= 2 * 104

int trapRainWater(vector<vector<int>>& heightMap)
{
    //1.把外围的点放到优先队列,优先队列把最小优先出队
    //2.每天点都要四个方面都要访问

    typedef pair<int, int> qp;
    priority_queue<qp, vector<qp>, greater<qp> >que;//从小到大排序
    vector<int> direction = { -1,0,1,0,-1 };//左、上、右、下

    int row = heightMap.size();
    int col = heightMap[0].size();
    vector<vector<bool>>visitedVec(row, vector<bool>(col, false));
    

    //
    for (int i = 0; i < row; i++)
    {
        for (int j = 0; j < col; j++)
        {
            if (true == visitedVec[i][j])
            {
                continue;
            }
            if (i == 0 || i == row - 1 || j == 0 || j == col - 1)//外围点保存
            {
                que.push(qp{ heightMap[i][j],i*col + j });
                visitedVec[i][j] = true;
            }
        }
    }

    int result = 0;
    while (!que.empty())
    {
        qp top =que.top();
        que.pop();
        int nx = top.second / col;
        int ny = top.second % col;
        for (int k = 0; k < 4; k++)
        {
            int x = nx+direction[k];
            int y = ny+direction[k + 1];
            if (x == 0 || x == row - 1 || y == 0 || y == col - 1)//外围
            {
                continue;
            }
            if (x<0 || x> row - 1 || y<0 || y>col - 1)//超出范围
            {
                continue;
            }
            if (visitedVec[x][y] == true)
            {
                continue;
            }
            if (heightMap[x][y]>top.first)
            {
                que.push(qp{ heightMap[x][y],x*col + y });
                visitedVec[x][y] = true;
            }
            else
            {
                result += top.first - heightMap[x][y];
                heightMap[x][y] = top.first;
                que.push(qp{ heightMap[x][y],x*col + y });
                visitedVec[x][y] = true;
            }
        }
    }
    return result;

}