实例
投币寄物柜是这样使用的:
- 首先,将物品放人寄物柜中。然后,投入硬币并拔出钥匙,就可以将寄物柜关闭了。关闭后的寄物柜,没有钥匙是无法打开的。
- 只要有硬币,任何人都可以关闭寄物柜,但寄物柜一旦被关闭,再怎么投币也无法打开。
- 打开寄物柜需要使用钥匙,而不是硬币。
因此我们可以说,硬币是关闭寄物柜的密钥,而钥匙则是打开寄物柜的密钥。
密钥配送问题
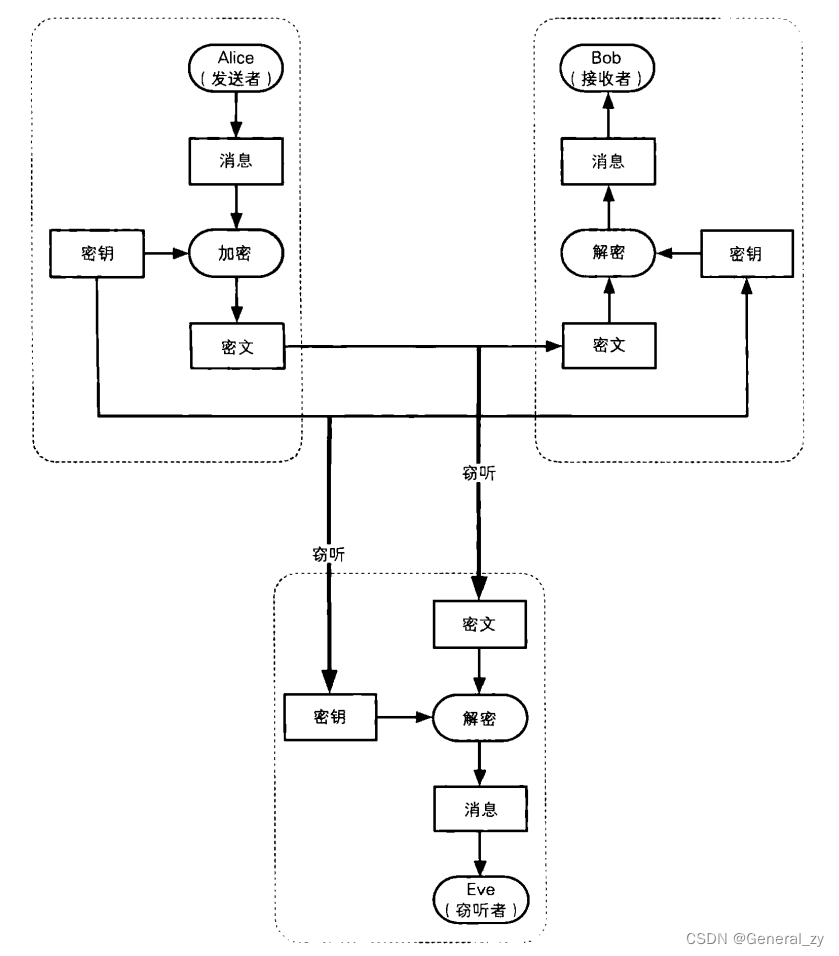
将邮件加密后发送到接收者,但密钥要如何告诉接收者呢?
如果密文和密钥都通过邮件发送,两者就都会被窃听者 Eve 窃听到。这样一来,同时得到密文和密钥的 Eve 就能够像Bob —样完成密文的解密并看到明文的内容了。也就是说,如果同时发送密钥,则 Eve 也能够完成解密。
解决方案
- 通过事先共享密钥来解决:在人数很多的情况下,通信所需要的密钥数量也会
增大,最终级别可能上千万 - 通过密钥分配中心来解决:随着员工数量的增加,密钥分配中心的负荷也会随之增加。如果密钥分配中心计算机发生故障,全公司的加密通信就会瘫痪。
- 通过 Diffie-Hellman 密钥交换来解决密钥配送问题:根据所交换的信息,双方可以各自生成相同的密钥,而窃听者 Eve 却无法生成相同的密钥。Eve 虽然能够窃听到双方所交换的信息,但却无法根据这些信息生成和双方相同的密钥。
- 通过公钥密码来解决密钥配送问题:在对称密码中,加密密钥和解密密钥是相同的,但公钥密码中,加密密钥和解密密钥却是不同的。只要拥杳加密密钥,任何人都可以进行加密,但没有解密密钥是无法解密的。因此,公钥密码的一个重要性质,就是只有拥有解密密钥的人才能够进行解密。接收者事先将加密密钥发送给发送者,这个加密密钥即便被窃听者获取也没有问题。发送者使用加密密钥对通信内容进行加密并发送给接收者,而只有拥有解密密钥的人( 即接收者本人 )才能够进行解密。这样一来,就用不着将解密密钥配送给接收者了,也就是说,对称密码的密钥配送问题,可以通过使用公钥密码来解决。
公钥密码
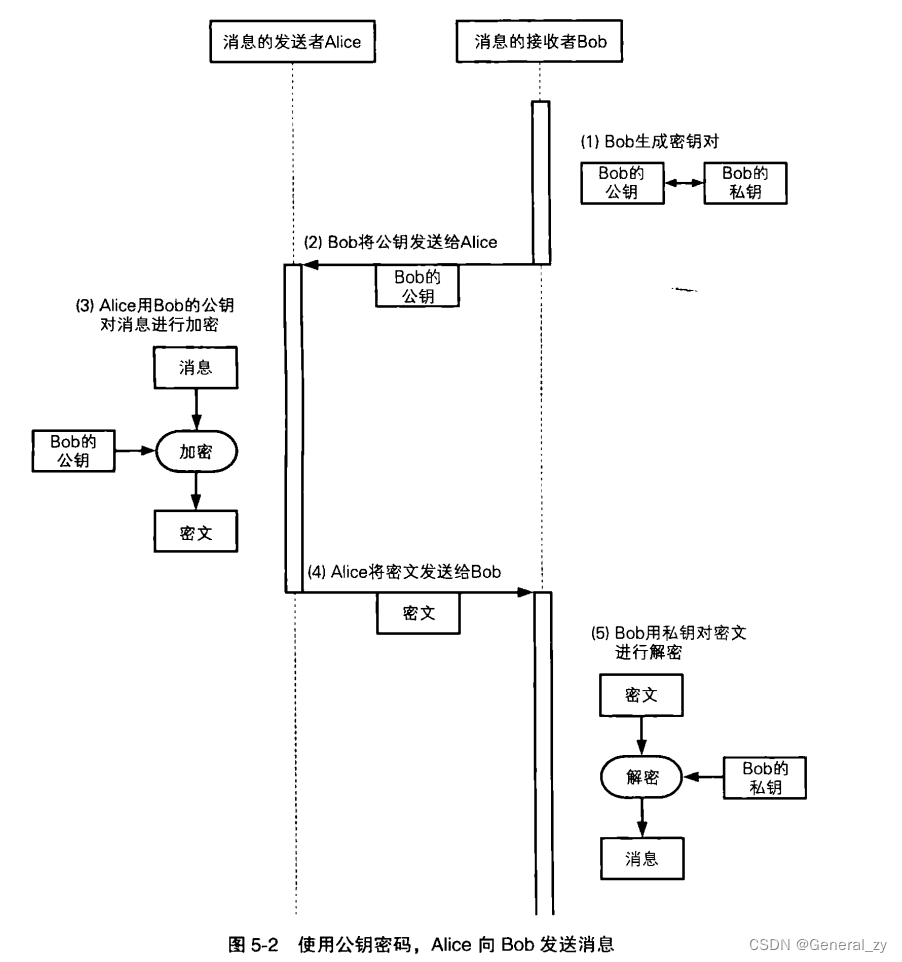
- 公钥密码( public-key cryptography )中,密钥分为加密密钥和解密密钥两种。
- 发送者用加密密钥对消息进行加密,接收者用解密密钥对密文进行解密。
- 要理解公钥密码,清楚地区分加密密钥和解密密钥是非常重要的。加密密钥是发送者加密时使用的,而解密密钥则是接收者解密时使用的。
- 也就是说,解密密钥从一开始就是由接收者自己保管的,因此只要将加密密钥发给发送者就可以解决密钥配送问题了,而根本不需要配送解密密钥。
公钥密码无法解决的问题
公钥密码解决了密钥配送问题,但这并不意味着它能够解决所有的问题,因为我们需要判断所得到的公钥是否正确合法,这个问题被称为公钥认证问题。
mod 运算
为 “除法求余数的运算” 定义一个运算符,即mod
RSA
RSA 是一种公钥密码算法,它的名字是由它的三位开发者,即 RonRivest 、 Adi Shamir 和Leonard Adleman 的姓氏的首字母组成的( Rivest-Shamir-Adleman )。
RSA 加密
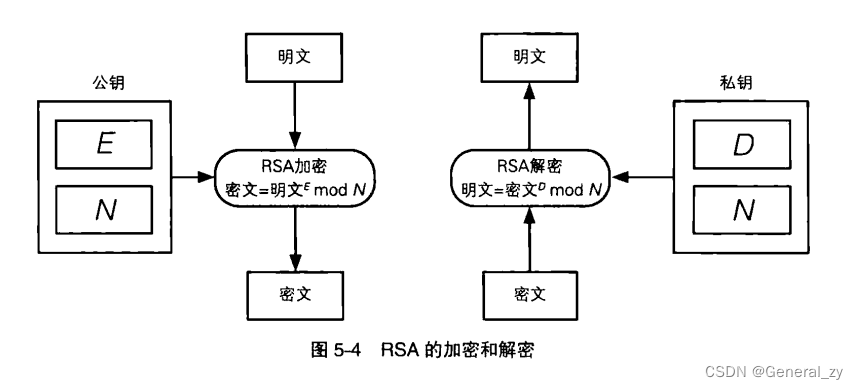
仅仅对明文进行乘方运算并求 mod 即可,这就是整个加密的过程。
密文 = 明文的E次方 mod N ( RSA 加密 )
其中,E和W是 RSA 加密的密钥,也就是说,E和N的组合就是公钥。
E 和N 这两个数并不是密钥对( 公钥和私钥的密钥对 )。E和N两个数才组成了一个公钥,因此我们一般会写成 “公钥是(E,N)” 或者"公钥是{E,N}” 这样的形式。
RSA 解密
数 D 和数 N 组合起来就是 RSA 的解密密钥,因此 D 和 N 的组合就是私钥。
明文 = 密文的D次方 mod N ( RSA 解密 )

生成密钥对
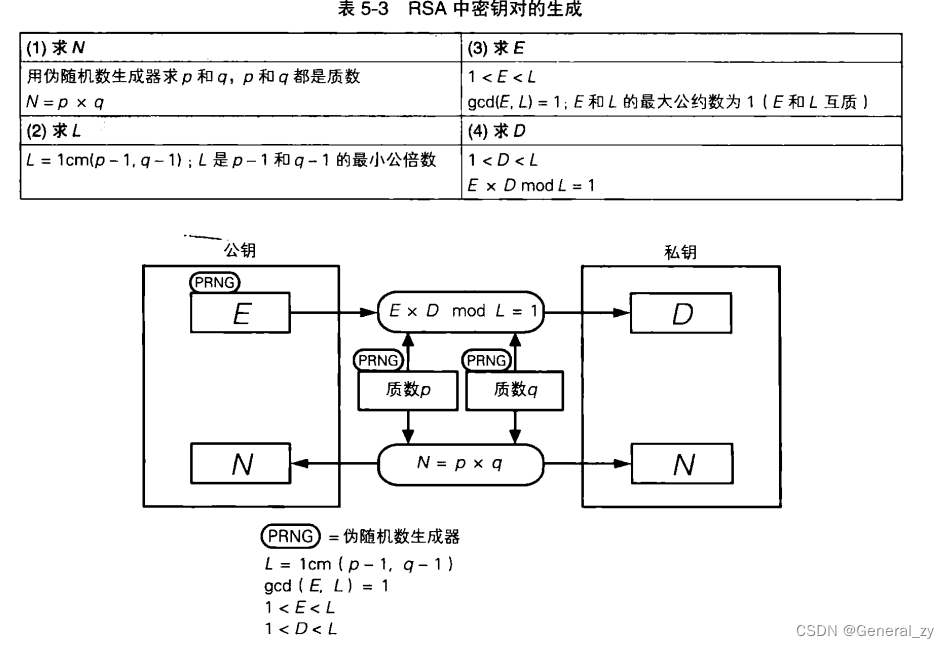
由于 E 和 N是公钥,D 和 N 是私钥,因此求 E、D 和 N 这三个数就是生成密钥对。RSA 密钥对的生成步骤如下。
(1) 求 N
(2) 求 L 是仅在生成密钥对的过程中使用的数 )
(3) 求 E
(4) 求 D
安全隐患
要防御中间人攻击,还需要一种手段来确认所收到的公钥是否真的属于 Bob, 这种手段称为认证,在这种情况
下,我们可以使用公钥的证书。
其他公钥密码
- ElGamal方式
- Rabin 方式
- 椭圆曲线密码:椭圆曲线密码( Elliptic Curve Cryptography, ECC )是最近备受关注的一种公钥密码算法。
它的特点是所需的密钥长度比 RSA 短。椭圆曲线密码是通过将椭圆曲线上的特定点进行特殊的乘法运算来实现的,它利用了这种乘法运算的逆运算非常困难这一特性






![[Database] 脏读、幻读这些都是什么?事务隔离级别又是什么?MySQL数据库的事务隔离级别都有哪些?](https://img-blog.csdnimg.cn/0b42b3bc46874658a5c93fe5e8c41c09.png)

![[ vulhub漏洞复现篇 ] Apache Solr RemoteStreaming 文件读取与SSRF漏洞 (CVE-2021-27905)](https://img-blog.csdnimg.cn/28832ea87c804360b84daca5bde7768e.png)