目录
编辑
贪心算法简介
什么时候使用贪心算法
贪心算法缺陷
贪心算法应用
贪心算法JAVA代码实现
贪心算法简介
贪心算法(又称贪婪算法)Greedy Algorithm 是一种不断做出局部最优解的选择,最终期望得到全局最优解的算法。
简单地说,贪心算法就是在每一步都做出当前最优的选择,以期望能够得到全局最优的解。
贪心算法是一种常用于求解优化问题的算法,在实际应用中,它常被用于求解一些经典问题,如背包问题、最短路径问题、最小生成树问题等。
其中贪心算法最佳实践为用于压缩数据的霍夫曼编码(Huffman encoding)还有用于寻找图中最短路径的Dijkstra算法。
什么时候使用贪心算法
贪心算法的优点是简单、高效,容易理解和实现。但同时,由于贪心算法是基于局部最优决策的,无法保证全局最优解,所以有一定的局限性。在实践中,贪心算法通常适用于满足以下两个条件的优化问题:
- 贪心选择性质:通过在每一步中选择最优选项(比如最小值或最大值),可以达到全局(整体)最优解。
- .最优子结构性质:如果整个问题的最优解包含子问题的最优解,则该问题具有最优子结构。
如果上面两个性质都成立,则可以使用贪心算法来解决问题。
贪心算法缺陷
由于贪心算法每次只考虑局部最优解,所以它无法保证能够得到全局最优解。在某些情况下,贪心算法会得到次优解甚至无解。比如下面的这一个例子。
在下面的示例中通过贪心算法寻求找到和最大数值的路径。它通过在每一步选择最大的可用数字来实现这一点。然而,贪心算法无法找到最大的和,因为它只根据每一步所掌握的信息做出决策,而不考虑整体问题。
示例1:
在下面的图中,贪心算法试图找到最大的一个数字。它在算法的每一步中选择最大的数字。我们一眼就可以看出该算法不会得到正确的解决方案。
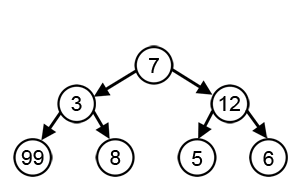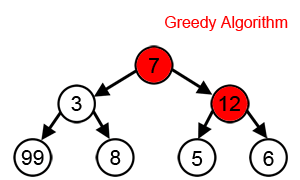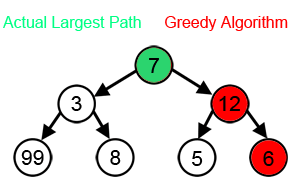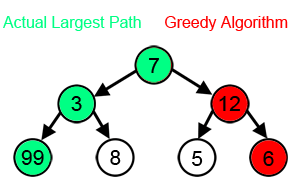
正确的解决方案是什么?为什么贪婪算法不适合这个问题?

正确的找到最大数值的路径为( 7,3,1,99) 那为什么使用贪心算法不能正确的得到答案呢?因为贪心算法总是每一步去选取最大数字的路径然后沿着此路径一直寻找下去。使用贪心算法的路径为( 7 -> 12 ->6 ->9)
示例2:
此示例和上面的示例一样,在此不在赘述,大家自行理解即可。
贪心算法应用
这里我们讲解一个使用 Dijkstra's algorithm(迪杰斯特拉算法)算法来寻找图中节点之间的最短路径。
Dijkstra算法用于在图中查找节点之间的最短路径。该算法维护一组未访问的节点,并计算从给定节点到另一个节点的暂定距离(这个距离时临时的后面有更短的再更新)。
如果算法发现了一种到达给定节点的更短路径,则将之前的路径更新至更短的路径。
此问题具有令人满意的优化子结构,因为如果A连接到B,B连接到C,并且路径必须通过A和B才能到达目的地C,则从A到B的最短路径和从B到C的最短路径必须是从A到C的最短路径的一部分。因此,子问题的最优解最终形成了最终的最优解,这正是贪心算法的典型应用。
请大家在看下面的图,大家找出从 A到B最短的距离。
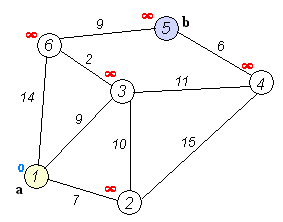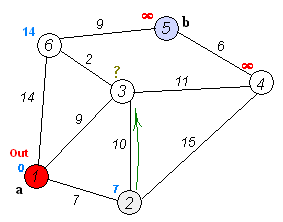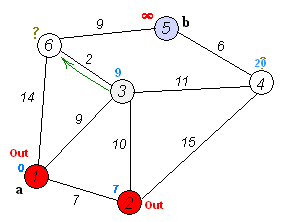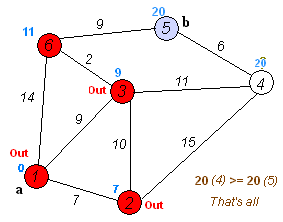
在这里我们要分开多步进行探索,通过每一步找出最小路径,然后最终找到最优的路径,下面是找解的一个过程。
- 起点 ① 出发,相邻的节点为 ②(7) ③(9) ⑥(14),很明显 ② ① 节点距离最短为 7
- 起点② 出发,相邻的节点为 ② ③(10) ② ④(15) ,那么③① (7+10 = 17) ④①(7+15=22) ,而③直接到①的距离为9 所以 ③① 节点为最短距离,值为9。
- 起点 ③(9) 出发,相邻节点 ③④(9+11=20) ③⑥(9+2=11) 故 ⑥ 节点为到①节点最短距离 值为11
- 起点⑥(11) 出发 相邻节点 ⑥⑤(11 +9 = 20) ⑥①(11 +14 = 25),所以⑥⑤节点距离最短, 而 ⑤节点正是我们要到达的节点,所以a-b最短距离为 20
贪心算法JAVA代码实现
下面我们使用JAVA代码来完成上面的这个 Dijkstra's algorithm 从图中找到a-b最短距离。代码中有详细的注释,通俗易懂。
/**
* 用 Dijkstra 算法求解图中两节点间的最短距离
*/
public class ShortestDistance {
public static void main(String[] args) {
// 构造节点列表
List<Node> nodes = buildNodeList();
// 计算节点0和节点5之间的最短距离
int distance = shortDistance(nodes.get(0), nodes.get(4), nodes.size());
System.out.println("节点0 和 5 之间的最短距离是:" + distance);
}
/**
* 构造节点列表
* @return 节点列表
*/
public static List<Node> buildNodeList() {
List<Node> nodes = Arrays.asList(
new Node("1"),
new Node("2"),
new Node("3"),
new Node("4"),
new Node("5"),
new Node("6")
);
// 添加节点间距离
nodes.get(0).addEdge(nodes.get(1), 7);//1-2
nodes.get(0).addEdge(nodes.get(2), 9);//1-3
nodes.get(0).addEdge(nodes.get(5), 14);//1-6
nodes.get(1).addEdge(nodes.get(2), 10);//2-3
nodes.get(1).addEdge(nodes.get(3), 15);//2-4
nodes.get(2).addEdge(nodes.get(3), 11);//3-4
nodes.get(2).addEdge(nodes.get(5), 2);//3-6
nodes.get(3).addEdge(nodes.get(4), 6);//4-5
nodes.get(4).addEdge(nodes.get(5), 9);//5-6
return nodes;
}
/**
* 通过 Dijkstra 算法计算两个节点间的最短距离
* @param start 起始节点
* @param end 目标节点
* @param numsOfNodes 节点个数
* @return 起点到目标节点的最短距离
*/
public static int shortDistance(Node start, Node end, int numsOfNodes) {
// 记录每个节点到起始节点的距离,初始化为最大值
PriorityQueue<Node> pq = new PriorityQueue<>(numsOfNodes, Comparator.comparingInt(n -> n.distanceFromStart));
// 将起始节点到自身的距离设为 0 并加入队列
start.distanceFromStart = 0;
pq.offer(start);
// 使用 Dijkstra 算法计算最短路径
while (!pq.isEmpty()) {
// 取出为空的并且距离起点最近的节点
Node currentNode = pq.poll();
// 如果当前节点是目标节点,则返回当前节点到起点的距离
if (currentNode == end) {
return currentNode.distanceFromStart;
}
// 遍历当前节点的每个相邻节点并更新距离
for (Map.Entry<Node, Integer> neighbor : sortAdjacentNode(currentNode.adjacentDistance).entrySet()) {
Node adjacentNode = neighbor.getKey();
Integer adjacentDistance = neighbor.getValue();
// 计算经当前节点到该相邻节点的距离
int distanceFromStart = currentNode.distanceFromStart + adjacentDistance;
// 如果该距离比之前计算的距离更短,则更新距离
if (distanceFromStart < adjacentNode.distanceFromStart) {
// 如果该节点已经加入过队列,将其删除
if (adjacentNode.isInQueue){
pq.remove(adjacentNode);
}
//更新该节点距离及是否在队列中
adjacentNode.distanceFromStart = distanceFromStart;
adjacentNode.isInQueue = true;
// 将该相邻节点加入到队列中
pq.offer(adjacentNode);
}
}
}
// 如果没有找到路径,则返回-1
return -1;
}
/**
* 将邻接节点排序并返回
* @param adjacentNodes 邻接节点及其权值
* @return 排序后的邻接节点及其权值
*/
public static Map<Node, Integer> sortAdjacentNode(Map<Node, Integer> adjacentNodes) {
return adjacentNodes.entrySet().stream()
.sorted(Comparator.comparingInt(Map.Entry::getValue))
.collect(Collectors.toMap(
Map.Entry::getKey,Map.Entry::getValue,(e1,e2)->e1,LinkedHashMap::new
));
}
static class Node {
String name;
Map<Node, Integer> adjacentDistance;
Integer distanceFromStart = Integer.MAX_VALUE;
// 标记该节点是否加入队列
boolean isInQueue;
public Node(String name) {
this.name = name;
adjacentDistance = new HashMap<>();
}
/**
* 添加相邻节点的权重
* @param node 相邻节点
* @param distance 距离
*/
public void addEdge(Node node, Integer distance) {
this.adjacentDistance.put(node, distance);
node.adjacentDistance.put(this, distance);
}
@Override
public String toString() {
return "Node{"+this.name+"}";
}
}
}到此,贪心算法介绍完毕,希望大家在阅读完此篇文章之后,对于贪心算法能够有一个更深入的认识,感谢大家的阅读。如大家对于贪心算法有任何疑惑之处,请留言给我。