第六章彩色图像处理

6.1彩色基础

颜色特性：

亮度：表达了无色的强度概念
色调：光波混合中与波长有关的属性（即颜色）
饱和度：即相对纯净度，或一种颜色混合白光的数量。饱和度与所加白光成反比

光的混合：

6.2彩色基础

6.2.1RGB彩色模型

在RGB 彩色模型中表示的图像由3个分量图像组成，每种原色一幅分量图像。当送人RGB 监视器时，这3幅图像在屏幕上混合生成一幅合成的彩色图像。在RGB空间中，用于表示每个像素的比特数称为像素深度。考虑一幅RGB 图像，其中每一幅红、绿、蓝图像都是一幅8比特图像，在这种条件下，可以说每个RGB彩色像素[即(R, G, B)值的三元组]有24比特的深度(3个图像平面乘以每个平面的比特数)。术语全彩色图像通常用来表示一幅24比特的RGB 彩色图像。在24比特RGB图像中，颜色总数是 $2^8)^3=16777216$ 。在这里插入图片描述

6.2.2CMY和CMYK彩色模型

$\begin{bmatrix}C\\ M\\ Y\end{bmatrix}=\begin{bmatrix}1\\ 1\\ 1\end{bmatrix}-\begin{bmatrix}R\\ G\\ B\end{bmatrix}$

HSI颜色空间是从人的视觉系统出发，用色调（Hue）、色饱和度（Saturation）和亮度（Intensity）来描述色彩。HSI颜色空间可以用一个圆锥空间模型来描述。用这种描述HSI色彩空间的圆锥模型相当复杂，但确能把色调、亮度和色饱和度的变化情形表现得很清楚。

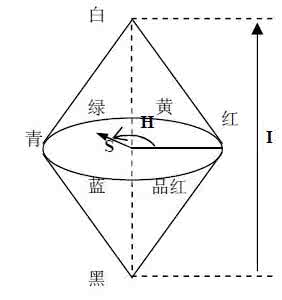
上图是HSI的双圆锥模型。模型中双圆锥的上顶点对应I=1，即白色；下顶点对应I=0，即黑色。色调（色相）用角度表示，0°表示红色，互补色相差180°。饱和度的取值范围从0到1，0对应于垂直轴的中心线（也就是说这条线上没有色彩，只有灰度），I=0.5时红色的饱和度为1，颜色空间中的点到I轴的距离即是其饱和度。

RGB转HSI：
给定一幅RGB彩色格式的图像，每个RGB像素的H分量可用下式得到： $H=\begin{cases}{\theta},\quad&B\leqslant G\\ 360-\theta,\quad&B>G\end{cases}$
其中， $\theta=\arccos\left[\frac{\frac{1}{2}[(R-G)+(R-B)]}{\left[(R-G)^{2}+(R-B)(G-B)\right]^{1/2}}\right]$
饱和度分量由下式给出： $S=1-\frac{3}{(R+{G}+B)}\big[\min(R,{G},{B})\big]$
最后，强度分量由下式给出： $I=\frac{1}{3}(R+G+B)$

HSI转RGB

RG扇区（ $0^{\circ}\leqslant H<120^{\circ}$ ）： $\begin{gathered}B=I\left(1-S\right) \\R=I\left[1+{\frac{S\cos H}{\cos(60^{\circ}-H)}}\right] \\G=3I-\left(R+B\right) \end{gathered}$
GB扇区（ $120^{\circ}\leqslant H<240^{\circ}$ ）： $\begin{gathered}H=H-120^{\circ}\\ R=I\left(1-S\right) \\ G=I\left[1+{\frac{S\cos H}{\cos(60^{\circ}-H)}}\right] \\ B=3I-(R+G) \end{gathered}$
BR扇区（ $240^{\circ}\leqslant H<360^{\circ}$ ）： $\begin{gathered}H=H-240^{\circ}\\ R=I\left(1-S\right) \\ G=I\left[1+{\frac{S\cos H}{\cos(60^{\circ}-H)}}\right] \\ B=3I-(G+B) \end{gathered}$

6.3伪彩色图像处理

6.3.1灰度分层

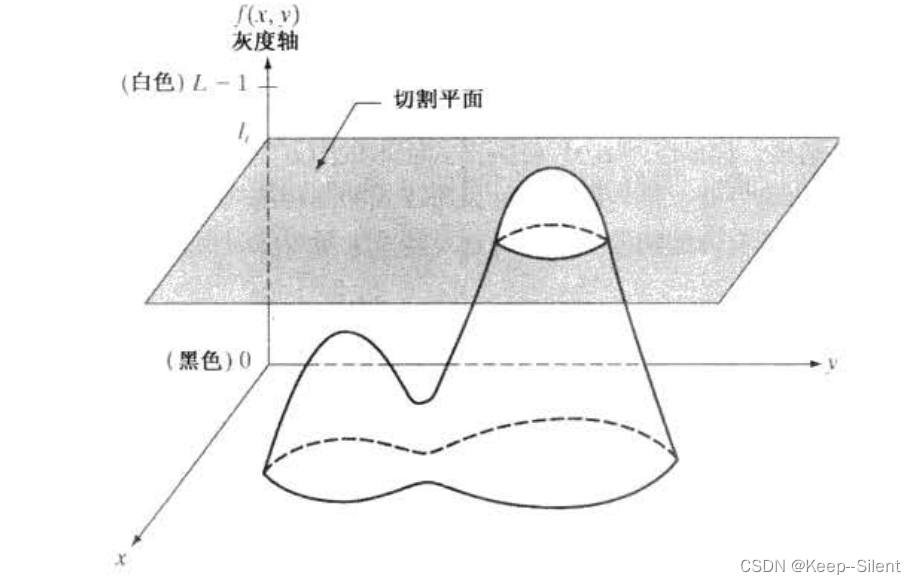
灰度分层(有时称为密度分层)和彩色编码技术是伪彩色图像处理的最简单的例子之一。如果一幅图像被描述为三维函数，则分层方法可以看成是放置一些平行于该图像的坐标平面的平面，然后,每个平面在相交的区域中“切割”图像函数。下图显示了使用位于f(x, y) =1处的一个平面把该图像函数切割为两部分的一个例子。
在这里插入图片描述

6.3.2灰度到彩色的变换

import cv2
import numpy as np
import matplotlib.pyplot as plt
import random
import math
import copy
def cv2_show(*args):
    for ttt in range(len(args)):
        img=args[ttt]
        cv2.imshow('img', img)
        cv2.waitKey(0)    
        cv2.destroyAllWindows() 

def plt_show(*args):
    for ttt in range(len(args)):
        img = args[ttt]
        if (len(img.shape) == 3):
            img = cv2.cvtColor(img, cv2.COLOR_RGB2BGR)
        elif (len(img.shape) == 2):
            img = cv2.cvtColor(img, cv2.COLOR_GRAY2RGB)
        plt.subplot(331+ttt), plt.imshow(img)

img=cv2.imread('zzx.jpg')
img2 = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
img3=cv2.cvtColor(img2, cv2.COLOR_GRAY2BGR)
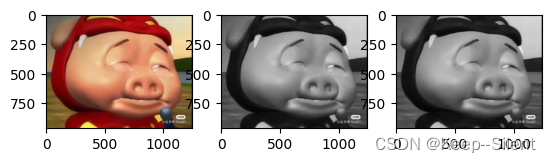
plt_show(img,img2,img3)

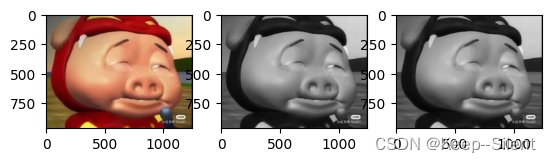
在这里插入图片描述

上图中分别是：彩图img，彩图转灰度图img2，灰度图转彩图img3
其中，彩图转灰度图时： $GR A Y = 0.3 * R + 0.59 * G + 0.11 * B$
而灰度图转彩图时： $[R, G, B] = [GR A Y, GR A Y, GR A Y]$

6.4全彩色图像处理基础

令c代表RGB彩色空间中的一个任意向量： $\mathcal{C}=\begin{bmatrix}c_R\\ c_G\\ c_B\end{bmatrix}=\begin{bmatrix}R\\ G\\ B\end{bmatrix}$
该式指出,c的分量仅是一幅彩色图像在一点处的RGB 分量。我们可以这样认为，彩色分量是坐标(x, y)的函数,表示为： $\mathcal{c}(x,y)=\begin{bmatrix}c_R(x,y)\\c_G(x,y)\\c_B(x,y)\end{bmatrix}=\begin{bmatrix}R(x,y)\\G(x,y)\\B(x,y)\end{bmatrix}$

6.5彩色变换

6.5.1公式

公式： $g(x,y)=T\left[f(x,y)\right]$
关键在于T的设计

6.5.2补色

img=cv2.imread('zzx.jpg')
K=255
n,m,o=img.shape
img2=copy.deepcopy(img)
for i in range(n):
    for j in range(m):
        for k in range(o):
            img2[i][j][k]=K-img[i][j][k]
plt_show(img,img2)

在这里插入图片描述

6.5.3彩色分层

对一幅彩色图像分层的最简方法之一是，把某些感兴趣区域之外的彩色映射为不突出的无确定性质的颜色。如果感兴趣的颜色由宽为w、中心在原型(即平均)颜色点并具有分量( $a_1, a_2,…,a_n$ )的立方体所包围，则必要的一组变换为

$s_i=\begin{cases} 0.5, &\Big[|r_j-a_j|>\frac{W}{2}\Big]_{1 \leq j \leq n}\quad i=1,2,\dots,n \\ r_i,& \mathrm{else}\end{cases}$

6.5.5直方图处理

def hist_show(img,name):#展示图片的直方图
    v=img.reshape(-1)
    n=len(v)
    plt.hist(v,weights=[1/n]*n,bins=64, alpha=0.5,label=name)
    plt.legend()
def getImgProbability(img):#  得到概率
    v=img.reshape(-1)
    n=len(v)
    k=1/n
    dt={i:0 for i in range(256)}
    for t in v:
        dt[t]+=k
    return [dt[t] for t in dt]
def histogramEqualization(img): #得到T(r)
    weight2=getImgProbability(img)
    for t in range(1,256):
        weight2[t]+=weight2[t-1]
    return [x*255 for x in weight2]
def imgHistogramEqualization(img):
    Tr=histogramEqualization(img)
    img_t=np.zeros(img.shape)
    for x in range(len(img)):
        for y in range(len(img[x])):
            img_t[x][y]=int(Tr[img[x][y]])
    return img_t.astype(np.uint8)

img=cv2.imread('me.jpg')
imgR,imgG,imgB=img[:,:,0],img[:,:,1],img[:,:,2]
print(imgR.shape)
imgR=imgHistogramEqualization(img[:,:,0])
imgG=imgHistogramEqualization(img[:,:,1])
imgB=imgHistogramEqualization(img[:,:,2])
img2= cv2.merge([imgR,imgG,imgB])
plt_show(img[:,:,0],img[:,:,1],img[:,:,2],
         imgR,imgG,imgB,
         img,img2)

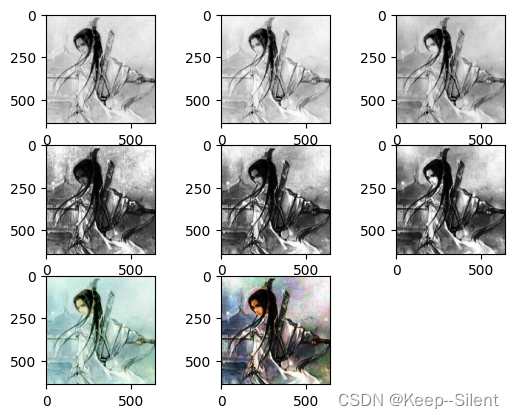
在这里插入图片描述

上图分别为：
原图R通道，原图B通道，原图G通道
R直方图均衡化，B直方图均衡化，G直方图均衡化
原图，原图直方图均衡化

hist_show(img[:,:,1],'Before')
hist_show(imgG,'After')

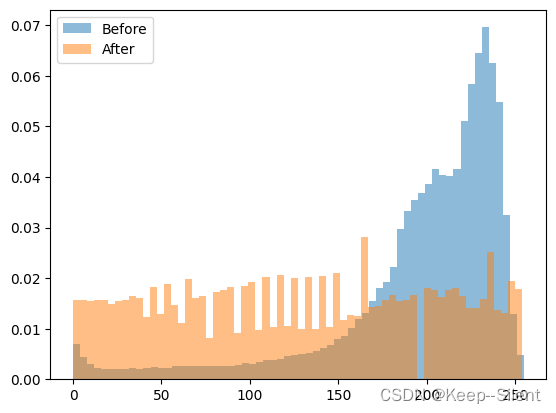
在这里插入图片描述

上图为原图G通道的直方图，和G通道直方图均衡后的直方图

同第三章的直方图处理一样，进行直方图均衡处理。不同点在于彩色是三通道（RGB），需要分别处理后进行合成。

6.6平滑和锐化

6.6.1彩色图像平滑

在一幅RGB彩色图像中，令 $S_{xy}$ 表示中心位于 $(x, y)$ 的邻域定义的一组坐标。在该邻域中RGB分量的向量平均值为 $\overline{\mathfrak{c}}(x,y)=\frac{1}{K}\sum_{(s,t)\in S_{s_{xy}}}{c}(s,t)$ 其遵循向量相加原则： $\overline{\mathcal{C}}(x,y)=\begin{bmatrix}\displaystyle \frac{1}{K}\sum_{(s,t)\in s_{xy}}R(s,t)\\ \displaystyle \frac{1}{K}\sum_{(s,t)\in s_{xy}}G(s,t)\\ \displaystyle \frac{1}{K}\sum_{(s,t) \in s_{xy}}B(s,t)\end{bmatrix}$

6.6.2彩色图像锐化

在第三章灰度变换与空间滤波中，已经提到过锐化，仅需将三通道分别处理后合并即可 $\nabla^2\left[c(x,y)\right] = \begin{bmatrix} \nabla^2R(x,y)\\ \nabla^2G(x,y) \\ \nabla^2B(x,y)\end{bmatrix}$

def WaveFilter(img,w):
    size=len(w)
    n,m=len(img),len(img[0])
    img2=np.zeros([n,m])
    img=np.pad(img,(size-1)//2)
    for x in range(n):
        for y in range(m):
            f=img[x:x+size,y:y+size]
            img2[x][y]=np.vdot(f,w) +img[x][y]         
            if img2[x][y]<0:
                img2[x][y]=0
            elif img2[x][y]>255:
                img2[x][y]=255
    img2=img2.astype(np.uint8)
    return img2

img=cv2.imread('caigou.jpg')
imgR,imgG,imgB=img[:,:,0],img[:,:,1],img[:,:,2]
print(imgR.shape)
imgR=WaveFilter(img[:,:,0],[[-1,-1,-1],[ -1,8,-1],[ -1,-1,-1]])
imgG=WaveFilter(img[:,:,1],[[-1,-1,-1],[ -1,8,-1],[ -1,-1,-1]])
imgB=WaveFilter(img[:,:,2],[[-1,-1,-1],[ -1,8,-1],[ -1,-1,-1]])
img2= cv2.merge([imgR,imgG,imgB])
plt_show(img[:,:,0],img[:,:,1],img[:,:,2],
         imgR,imgG,imgB,
         img,img2,img2-img)

在这里插入图片描述

上图分别为：
原图R通道，原图B通道，原图G通道
R拉普拉斯锐化，BR拉普拉斯锐化，GR拉普拉斯锐化
原图，原图R拉普拉斯锐化，原图和拉普拉斯锐化图相减

6.7基于彩色的图像分割

6.7.2RGB向量空间中的分割

欧式距离： $D(z,\boldsymbol{a})=\|z-\boldsymbol{a}\|=\left[(z-\boldsymbol{a})^{\text{T}}(\boldsymbol{z}-\boldsymbol{a})\right]^{\frac{1}{2}}=\left[(z_R-a_R)^2+(z_G-a_G)^2+(z_B-a_B)^2\right]^{\frac{1}{2}}$
给定一个任意的彩色点，如同采用距离公式那样，通过确定它是否在盒子表面或内部来进行分割。

6.8彩色图像中的噪声

通常,彩色图像的噪声内容在每个彩色通道中具有相同的特性,但噪声对不同的彩色通道所造成的影响不同。一种可能是个别通道的电子学故障。然而，不同的噪声水平像是由每个彩色通道的相对照射强度的差异造成的。例如,在CCD摄像机中红色滤镜的使用将减小用于红色传感器的照射强度。CCD传感器在低照明水平下就是噪声源，因此，这种情况下得到的RGB 图像的红色分量图像与其他两幅分量图像相比往往是噪声源。