算法拾遗三十三Morris遍历
- 常规二叉树遍历
- Morris遍历
- Morris遍历判断是否是搜索二叉树
- 给定一颗二叉树的头节点head,求以head为头的树中,最小深度是多少?
常规二叉树遍历
public static class Node {
public int value;
Node left;
Node right;
public Node(int data) {
this.value = data;
}
}
public static void process(Node root) {
if (root == null) {
return;
}
// 1 先序遍历
process(root.left);
// 2 中序遍历
process(root.right);
// 3 后序遍历
}
时间复杂度为O(N)
空间复杂度为O(M)树的高度
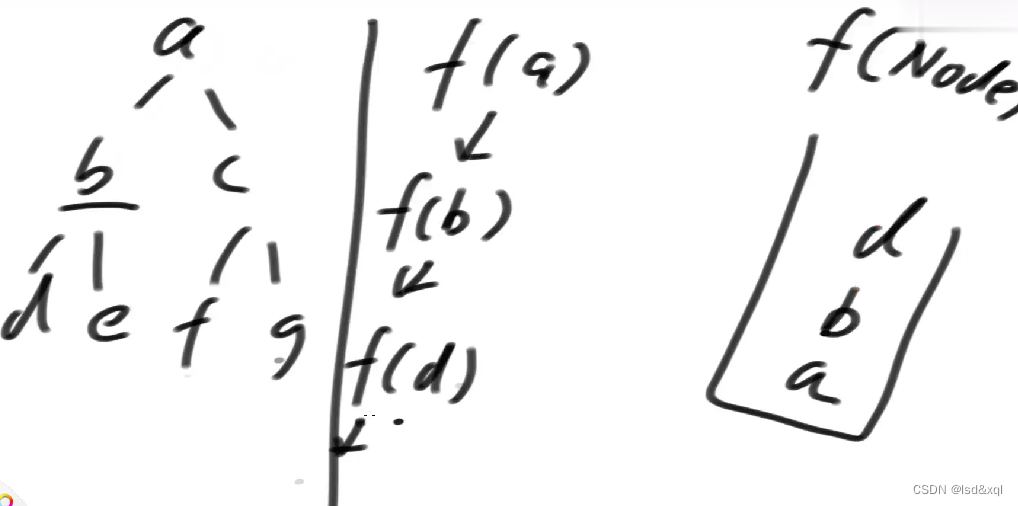
从一开始会依次调用f(a)->f(b)->f(d),到f(d)后的后续操作为空,返回。递归跑起来是因为有系统在内部进行压栈,看起来在代码层次没有申请空间,但是系统内部生成了这么一个系统栈来让整个递归跑起来。【栈的大小为二叉树的高度】
之前学的所有二叉树的遍历高度这个空间是省不掉的。
Morris遍历
可以实现时间复杂度为O(N),可以优化空间复杂度为O(1),利用了一棵树上大量的指针空闲空间来完成遍历。
遍历细节:

流程:
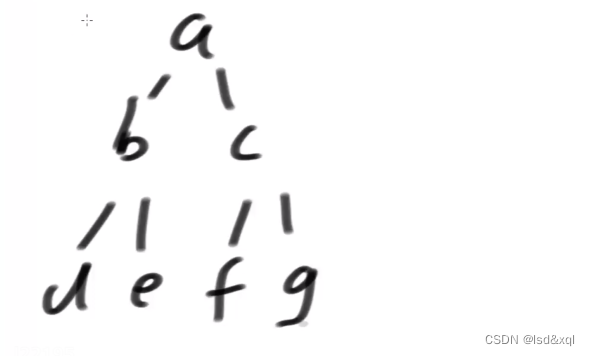
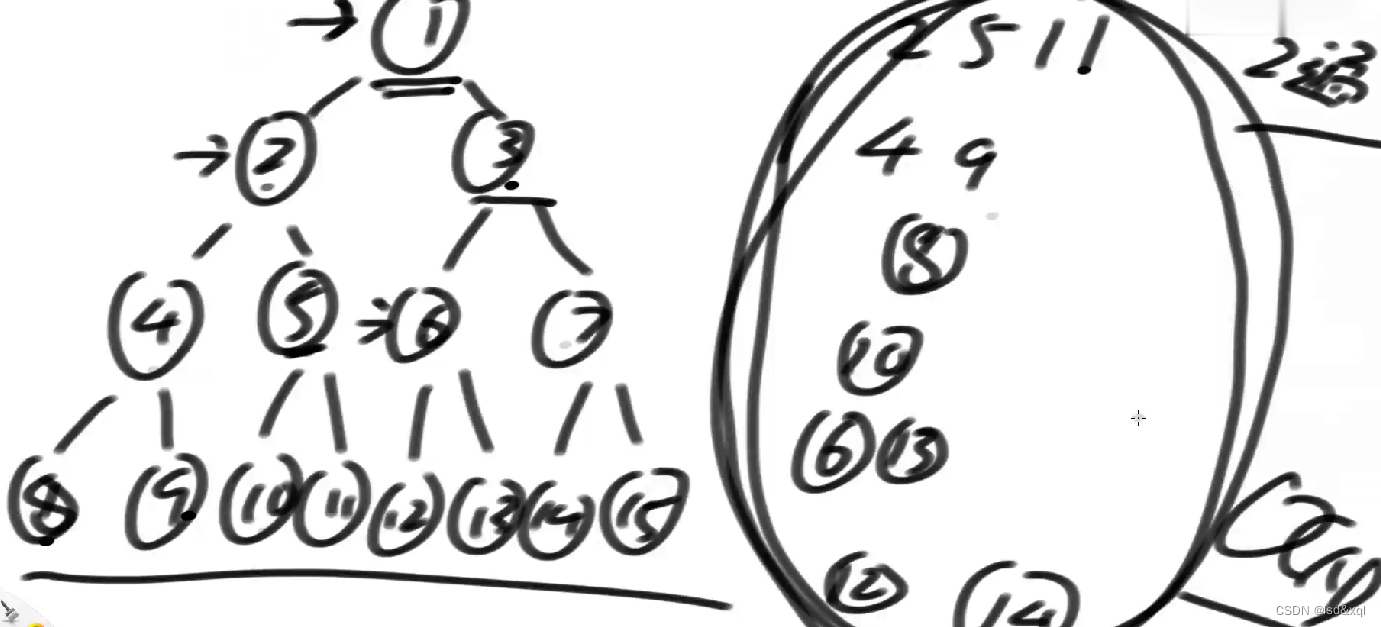
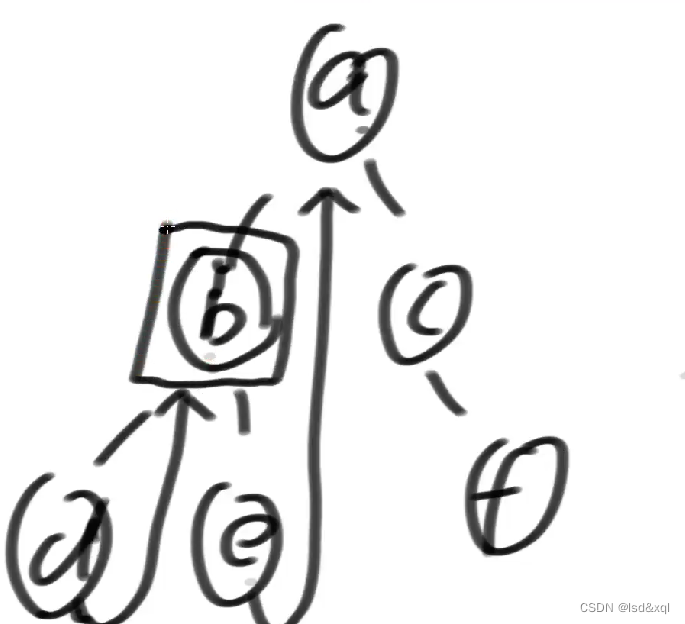
如上图例子
1、当前节点来到头节点的位置
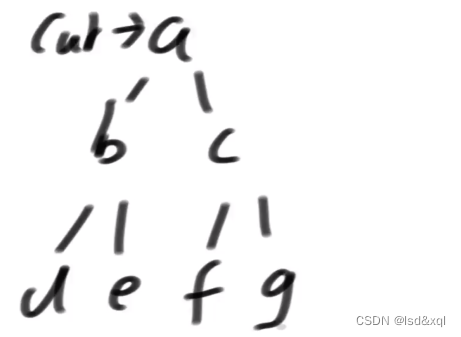
1)如果cur无左树,cur直接往右移动cur= cur.right。
2)如果cur有左树,则需要找到左树上的最右节点(mostRight),如果mostRight的右指针指向是空的,那么让它指向当前节点,然后cur向左移动。
如果mostRight的右指针是指向当前节点,这个时候让它指回空,然后cur向右移动
如上图例子:
1、首先cur是有左子树的
2、则找到左子树的最右节点e
4、e的右指针指向空的,让e指向cur
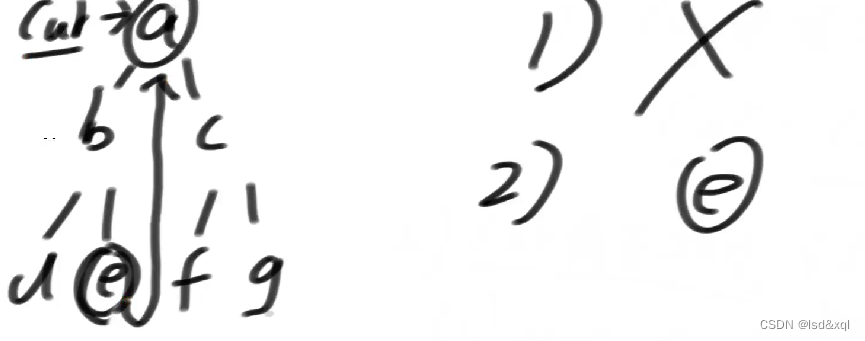
5、cur往左移动来到b
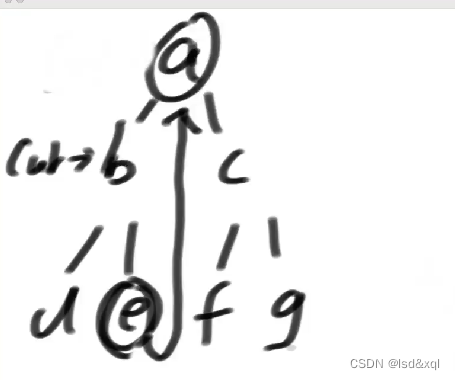
cur来到b后有左树,左树的最右节点为d,然后让d的右指针指向b
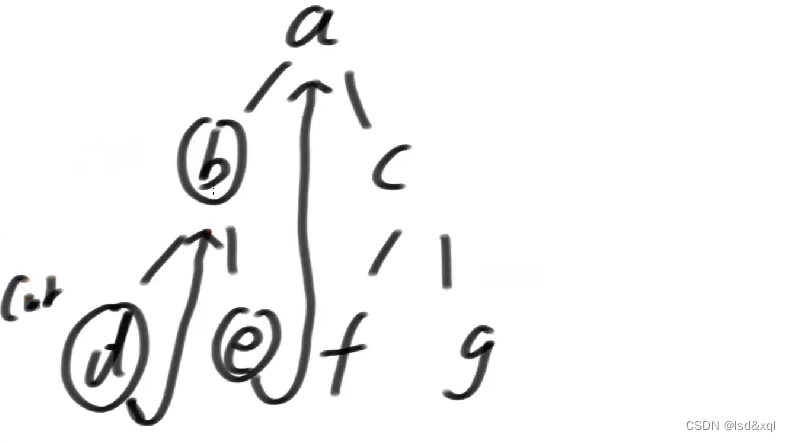
然后cur来到d位置。
然后d位置左子树为空,则cur向右移动,cur回到b
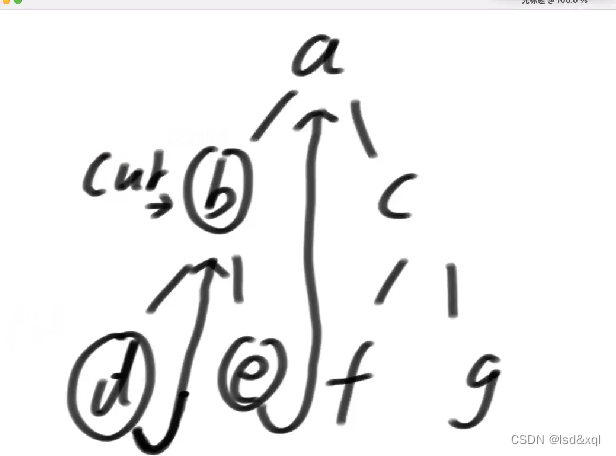
然后中了2)条件中的第二种情况【如果mostRight的右指针是指向当前节点,这个时候让它指回空,然后cur向右移动】,cur来到e
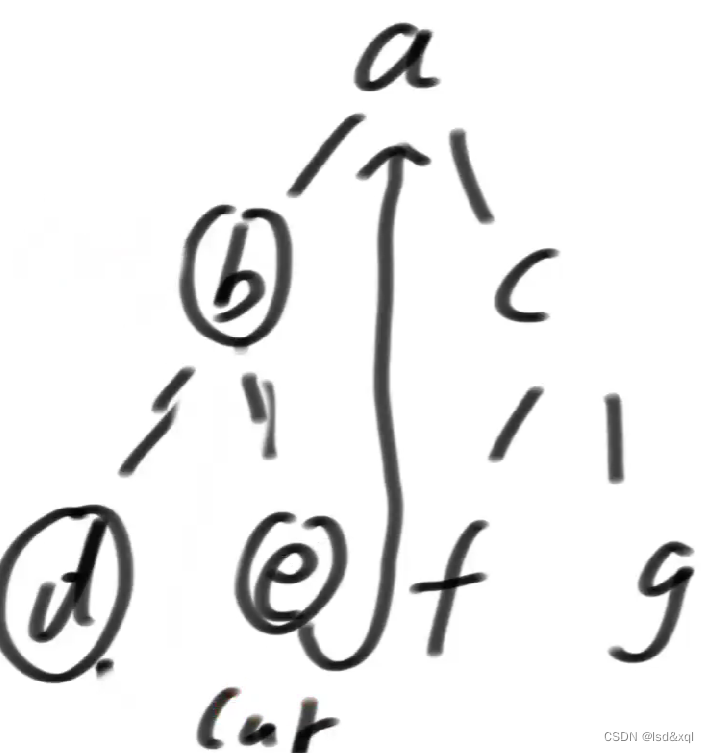
由于e没有左树,所以直接往右移动回到了a
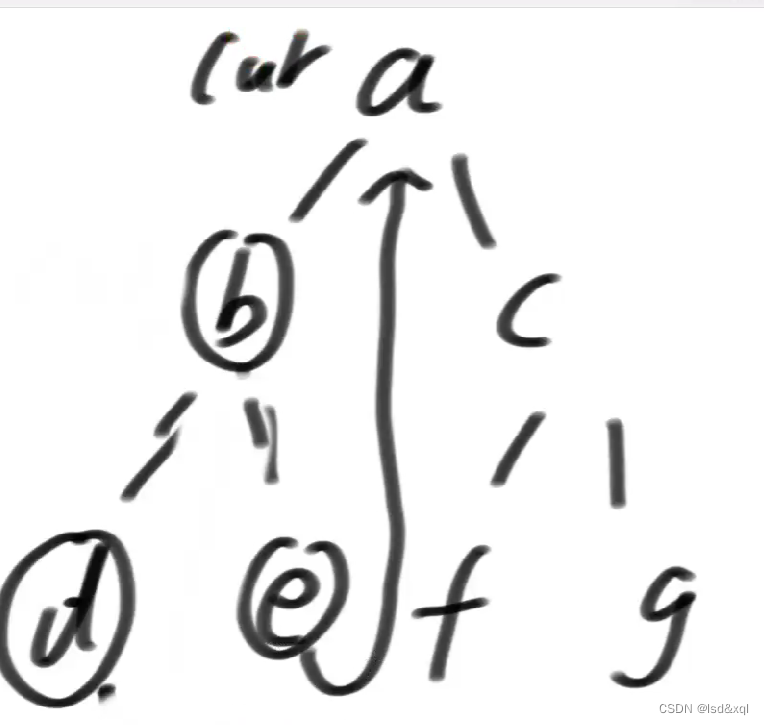
回到a之后,左树上的最右节点e,e的右指针指向了cur本身。把e指向a改为指向空,然后cur向右移动到c。直到最后移动完【发现每个节点一定都能遍历到】
遍历的顺序为:a,b,d,b,e,a,c,f,c,g
特点,任何一个节点有左树,那么这个节点一定到两次,如果某一个节点没有左树只会到一次
流程实质:
是在用左树上的最右节点的右指针状态来标记我到底是第一次到的这个节点还是第二次。
先序:
Morris加工先序:对于能回到自己两次的节点只打印第一次,对于只到达自己一次的节点只处理一次
先序:a,b,d,e,c,f,g
中序:
对于能回到自己两次的节点,则在第二次打印,对于只能回到自己一次的节点,则第一次打印
中序:d,b,e,a,f,c,g
public static class Node {
public int value;
Node left;
Node right;
public Node(int data) {
this.value = data;
}
}
public static void morris(Node head) {
if (head == null) {
return;
}
//cur指针初始在头节点
Node cur = head;
Node mostRight = null;
while (cur != null) {
//mostRight先来到左孩子
mostRight = cur.left;
if (mostRight != null) {
//如果左孩子不是空
//左树上的最右指针指向空和左树上的最右指针指向自己两种情况需停止
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
//如果mostRight的右指针指向空,让其指向cur,
// 然后cur向左移动(cur = cur.left)
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue;
} else {
//如果mostRight的右指针指向cur,让其指向null,
//然后cur向右移动(cur = cur.right)
mostRight.right = null;
}
}
//如果cur没有左孩子,cur向右移动(cur = cur.right)
cur = cur.right;
}
}
Morris遍历找左树的最右节点的时间复杂度之所以为O(N)是因为在遍历的过程中不会每个节点的左树最右节点不会出现重复
先序遍历
public static void morrisPre(Node head) {
if (head == null) {
return;
}
Node cur = head;
Node mostRight = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
//有左树第一次来的时候打印
System.out.print(cur.value + " ");
mostRight.right = cur;
cur = cur.left;
continue;
} else {
mostRight.right = null;
}
} else {
//如果没有左树,直接打印
System.out.print(cur.value + " ");
}
cur = cur.right;
}
System.out.println();
}
中序遍历
public static void morrisIn(Node head) {
if (head == null) {
return;
}
Node cur = head;
Node mostRight = null;
while (cur != null) {
mostRight = cur.left;
//如果当前节点没有左树直接跳过打印当前值
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
//如果当前节点要到两次,第一次到的时候已经continue了
//只有第二次来到自己要往右边走的过程才打印
continue;
} else {
mostRight.right = null;
}
}
System.out.print(cur.value + " ");
cur = cur.right;
}
System.out.println();
}
后续遍历:
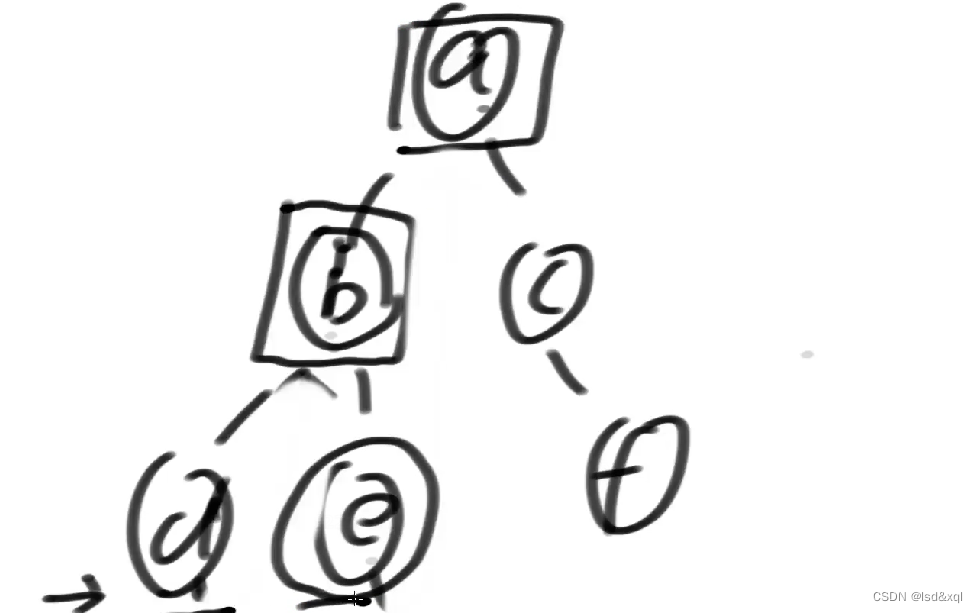
还是刚才的二叉树给定morris序列
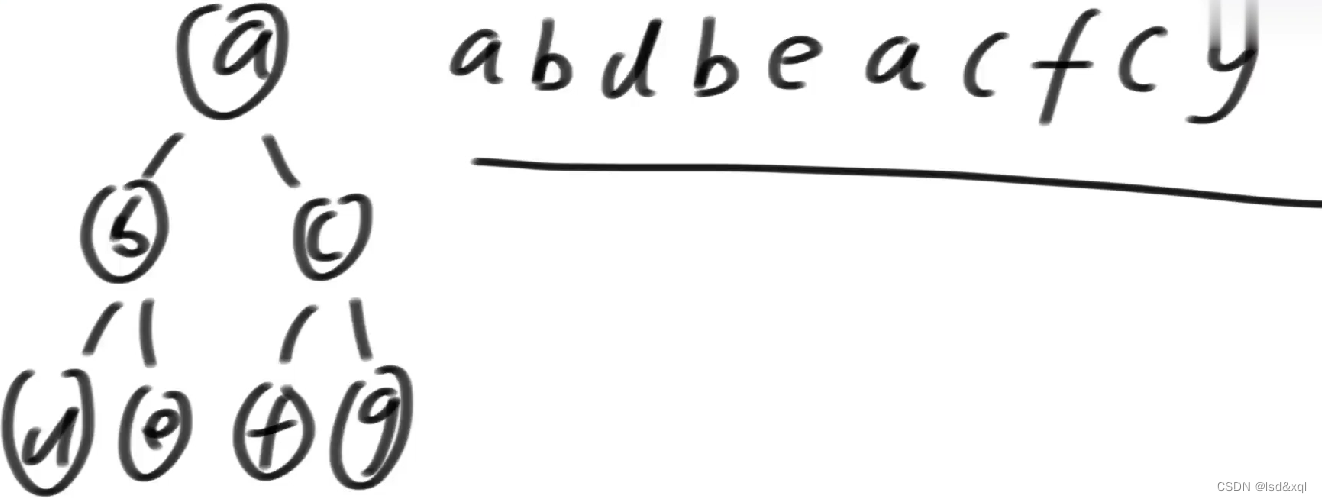
我们把处理时机只放在能回到自己两次的节点,然后在第二次回到自己的时候处理,如上图只对a,b,c做处理。
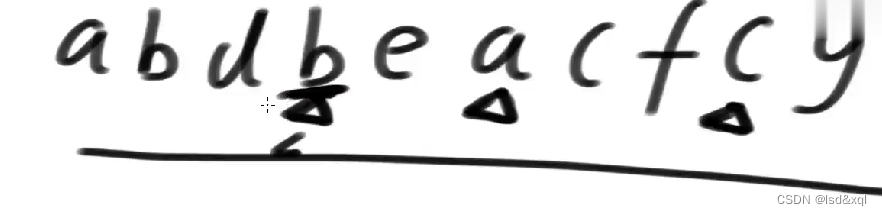
当来到要处理的节点的时候需要逆序的打印其左树的右边界。
d,e,b,f,g,c
public static void morrisPos(Node head) {
if (head == null) {
return;
}
Node cur = head;
Node mostRight = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue;
} else {
mostRight.right = null;
printEdge(cur.left);
}
}
cur = cur.right;
}
printEdge(head);
System.out.println();
}
public static void printEdge(Node head) {
Node tail = reverseEdge(head);
Node cur = tail;
while (cur != null) {
System.out.print(cur.value + " ");
cur = cur.right;
}
reverseEdge(tail);
}
public static Node reverseEdge(Node from) {
Node pre = null;
Node next = null;
while (from != null) {
next = from.right;
from.right = pre;
pre = from;
from = next;
}
return pre;
}
Morris遍历判断是否是搜索二叉树
public static boolean isBST(Node head) {
if (head == null) {
return true;
}
Node cur = head;
Node mostRight = null;
Integer pre = null;
boolean ans = true;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue;
} else {
mostRight.right = null;
}
}
//上一个节点的值不为空,且上一个节点的值大于当前节点的值,则不是搜索二叉树
if (pre != null && pre >= cur.value) {
//不能直接return false,因为此处直接返回morris遍历可能会将整棵树打乱
ans = false;
}
pre = cur.value;
cur = cur.right;
}
return ans;
}
给定一颗二叉树的头节点head,求以head为头的树中,最小深度是多少?
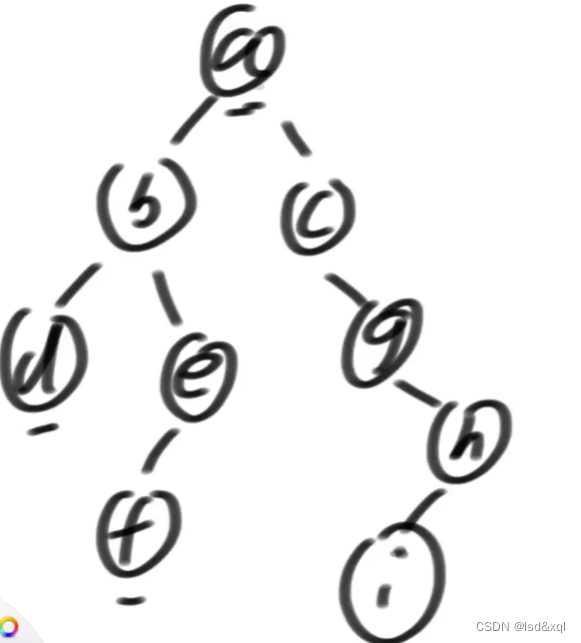
1、morris遍历cur来到任何节点的时候,这个level能够正确的更新出来到了第几层。
2、需要正确的发现叶子节点。
如果上面两个问题都解决了,那么问题解决。
如果知道x的层数,y是x的左孩子,那么y一定在x的下一层。
如果知道x的层数,y是x的右孩子,如果y左树上的最右节点指向非x那么y一定在x的下一层。如果是x
那么需要数一下它左树右边界上有几个节点,则用x的层数减去边界上的节点树,这样就解决了第一个问题。
第二个问题:如何发现所有的叶节点,对于能回到自己两次的节点,第二次回到的时候判断其下的是不是叶子节点:如第二次回到b判断d是否是叶子节点,第二次回到a恢复完后判断e是否是叶子节点,最后再判断整棵树的最右节点是否是叶子节点。
走一下流程:
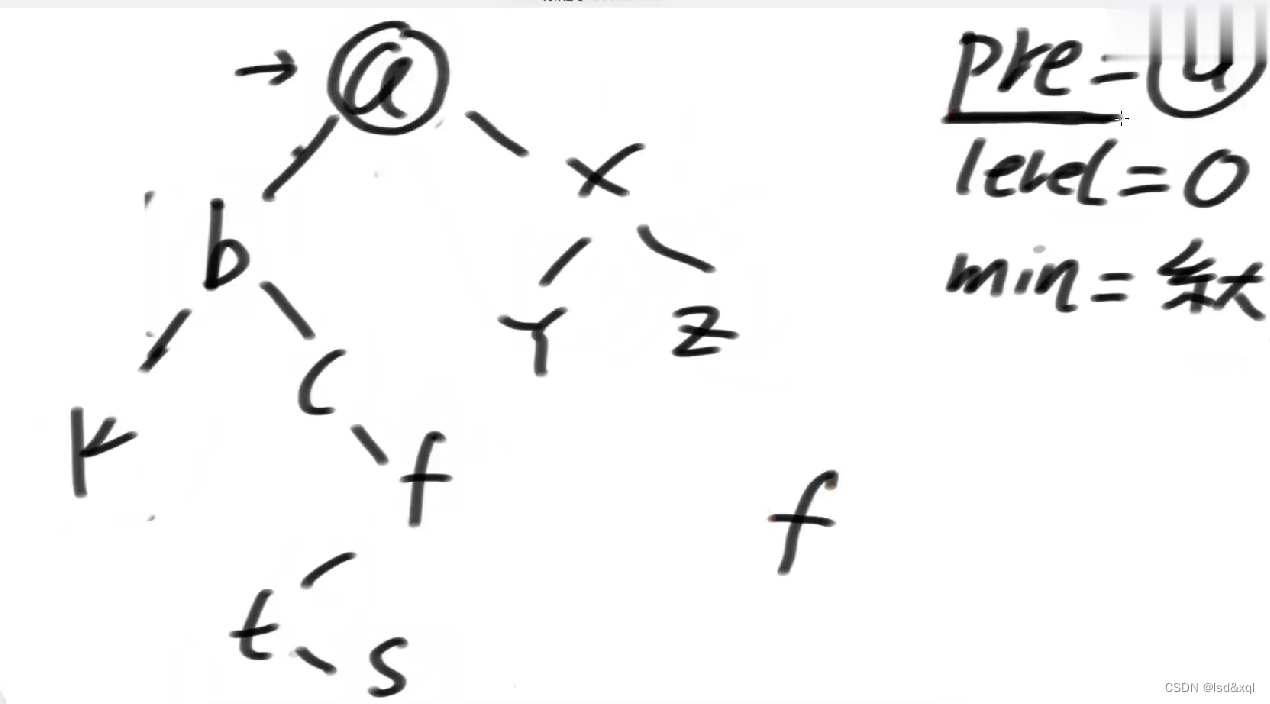
一开始pre = a
level = 0
min = 系统最大
首先a是找a左树的最右节点f,更新level为1,以及指向
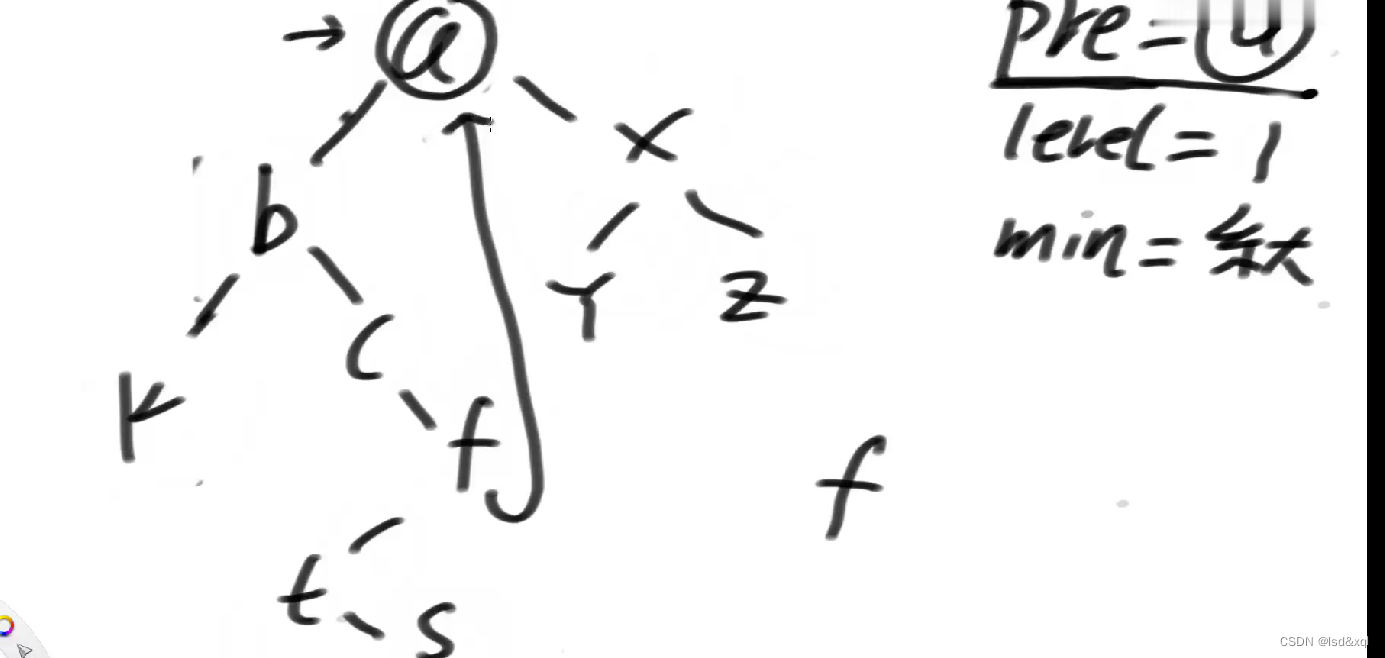
然后cur来到b
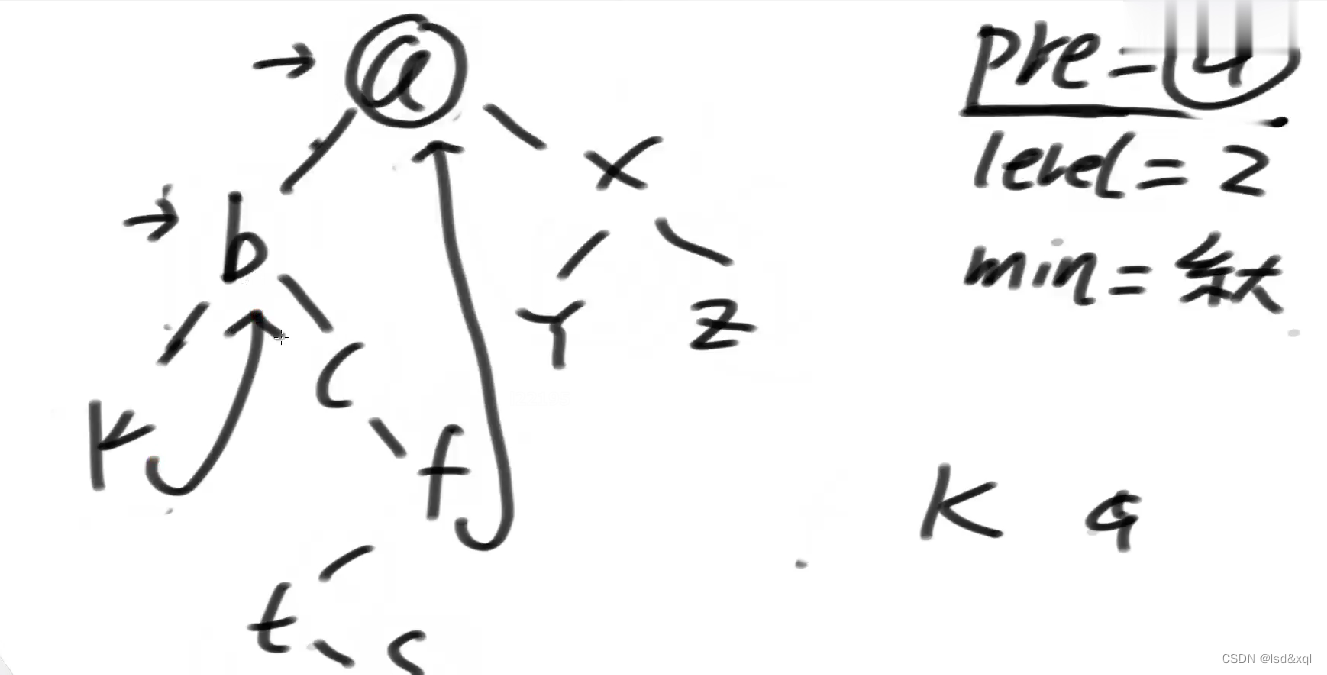
来到k,k左树的最右节点为空,不等于b,k的level是3
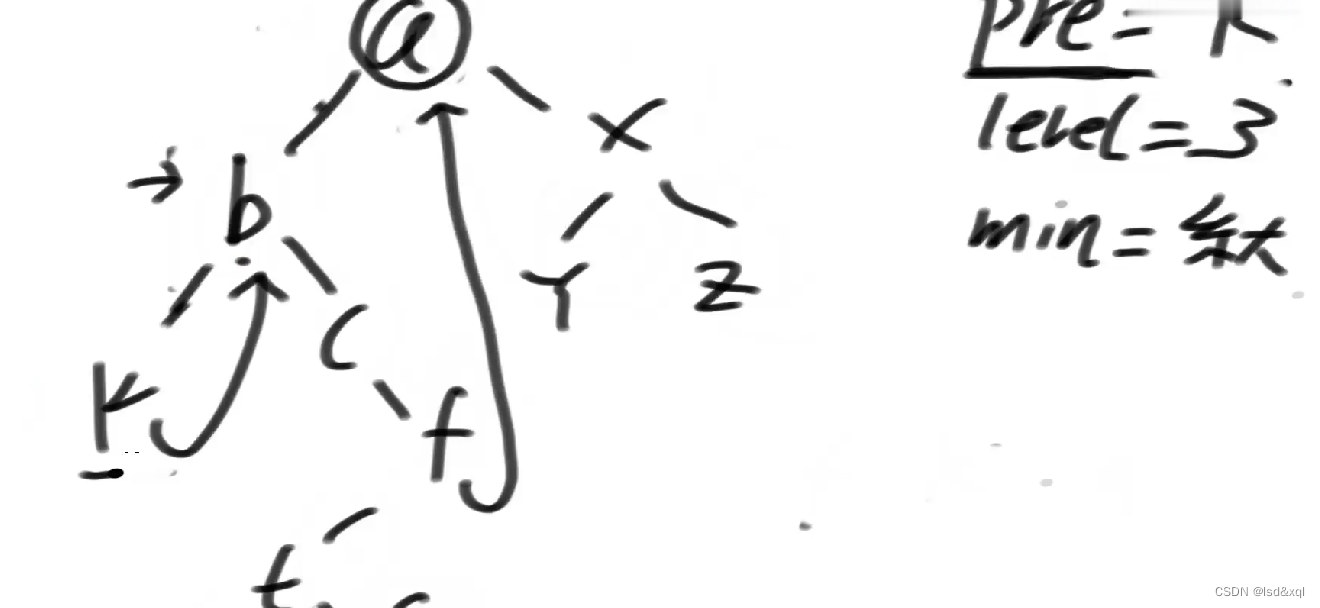
回到b,level = 2,然后更新min = 3
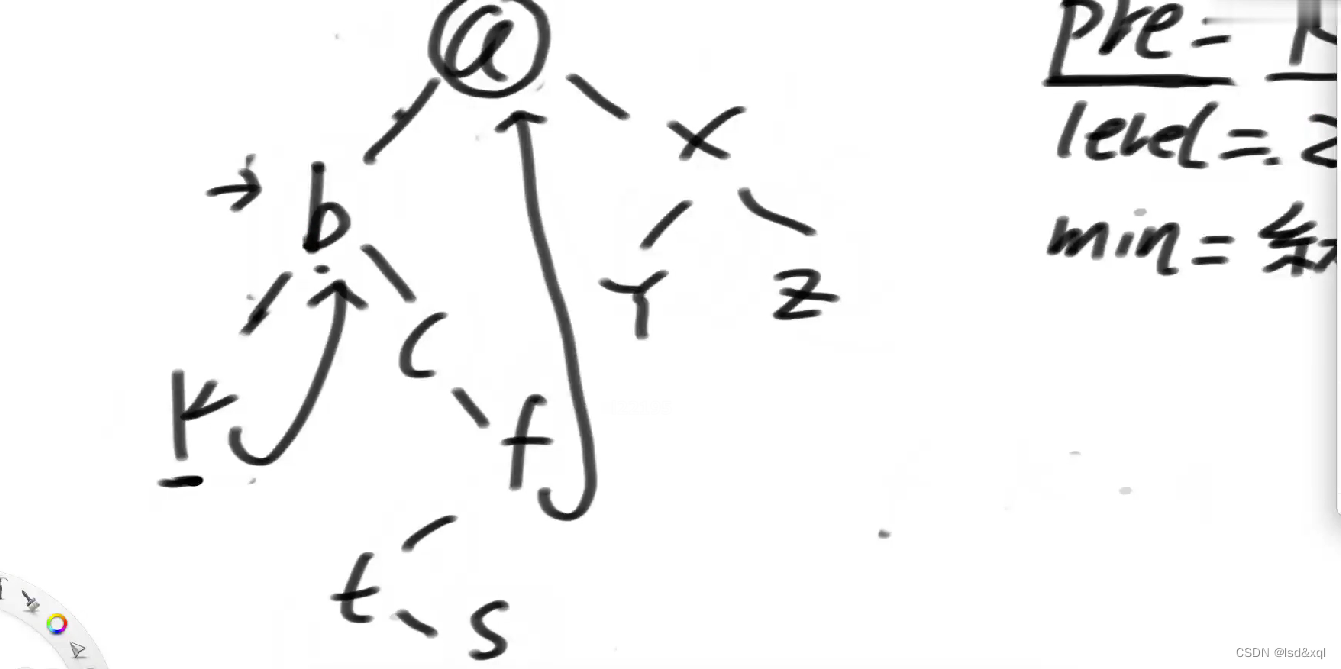
然后来到c
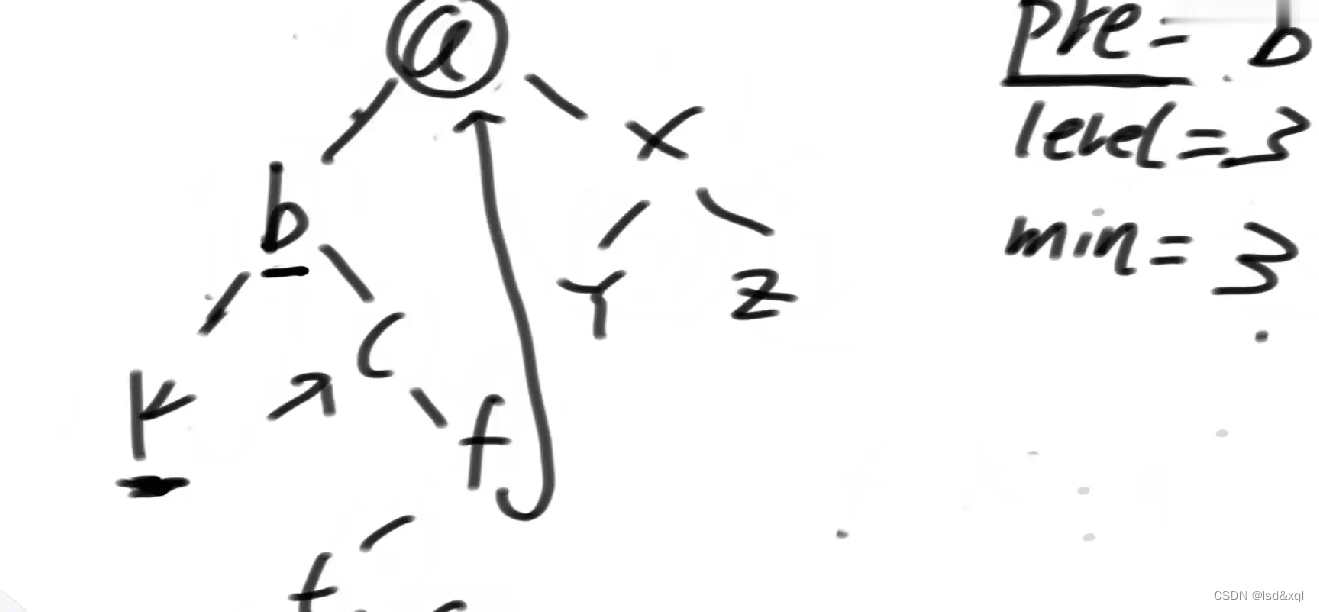
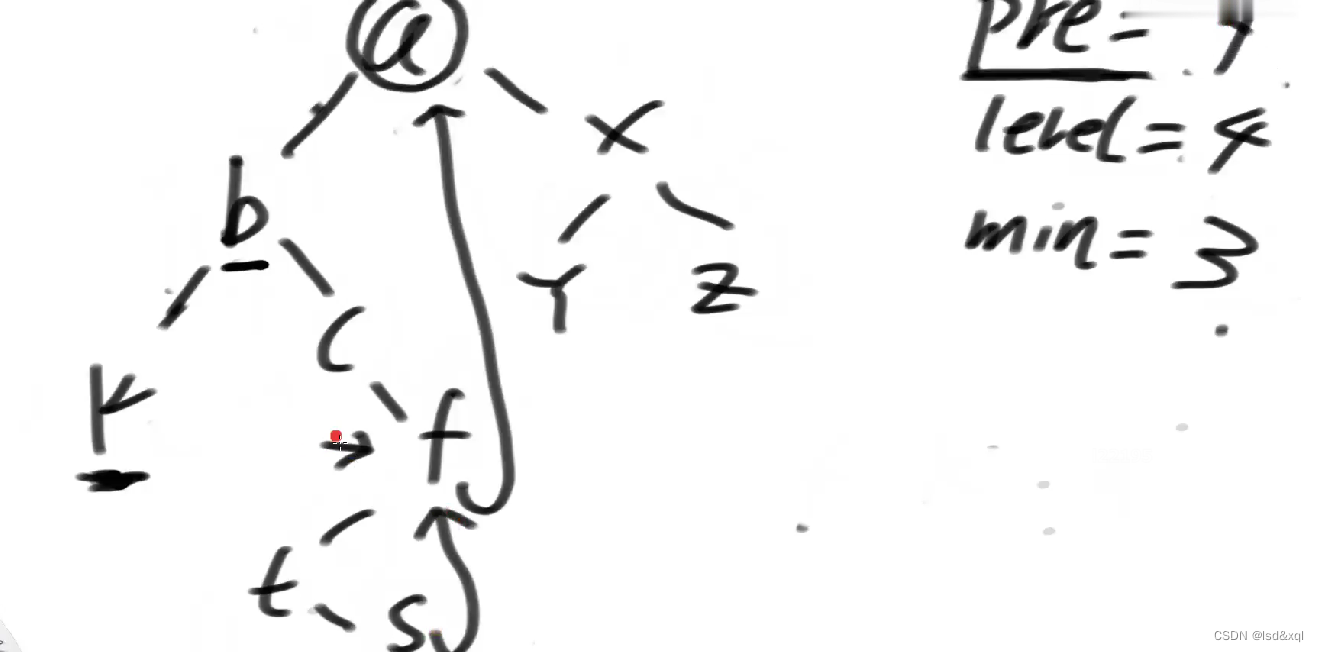
这样依次更新下去
// 本题测试链接 : https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/
public class MinDepth {
// 不提交这个类
public static class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int x) {
val = x;
}
}
// 下面的方法是一般解
public static int minDepth1(TreeNode head) {
if (head == null) {
return 0;
}
return p(head);
}
// 返回x为头的树,最小深度是多少
public static int p(TreeNode x) {
//x是叶节点,深度为1
if (x.left == null && x.right == null) {
return 1;
}
// 左右子树起码有一个不为空
int leftH = Integer.MAX_VALUE;
if (x.left != null) {
leftH = p(x.left);
}
int rightH = Integer.MAX_VALUE;
if (x.right != null) {
rightH = p(x.right);
}
return 1 + Math.min(leftH, rightH);
}
// 下面的方法是morris遍历的解
public static int minDepth2(TreeNode head) {
if (head == null) {
return 0;
}
TreeNode cur = head;
TreeNode mostRight = null;
int curLevel = 0;
int minHeight = Integer.MAX_VALUE;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
int rightBoardSize = 1;
while (mostRight.right != null && mostRight.right != cur) {
rightBoardSize++;
mostRight = mostRight.right;
}
if (mostRight.right == null) { // 第一次到达
curLevel++;
mostRight.right = cur;
cur = cur.left;
continue;
} else { // 第二次到达
if (mostRight.left == null) {
minHeight = Math.min(minHeight, curLevel);
}
curLevel -= rightBoardSize;
mostRight.right = null;
}
} else { // 只有一次到达
curLevel++;
}
cur = cur.right;
}
int finalRight = 1;
cur = head;
while (cur.right != null) {
finalRight++;
cur = cur.right;
}
if (cur.left == null && cur.right == null) {
minHeight = Math.min(minHeight, finalRight);
}
return minHeight;
}
}
总结:
如果需要信息的强整合,就不能用morris遍历,采用二叉树递归套路,如果不需要手机左右树的全部信息那么可以采用morris遍历






![[编程工具]Unity配表导出工具TableExporter1.1](https://img-blog.csdnimg.cn/84c930c42de44f9f8f042f227e2bda61.png)