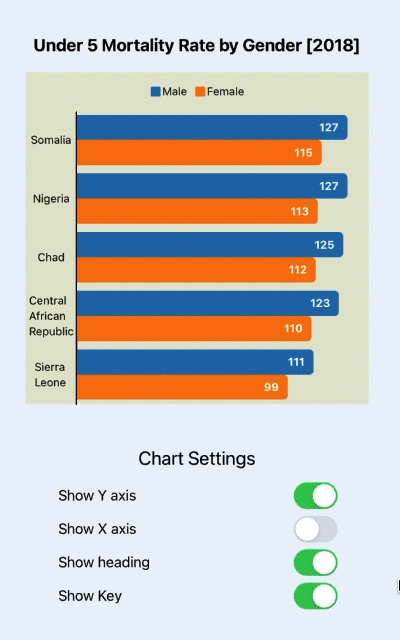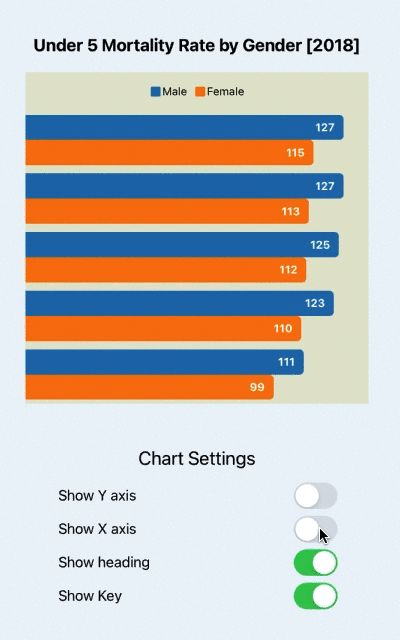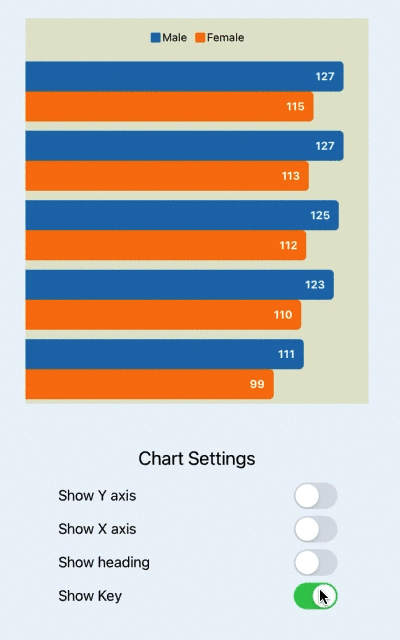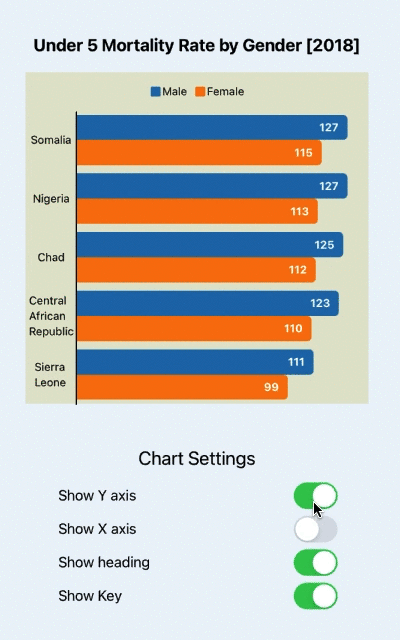
1.斐波那切数列套路

        1.1F(N)=F(N-1)+F(N-2)

        1.2F(N)=3F(N-1)-4F(N-3)+6F(N-5)

        1.3生牛问题

        1.4达标串数量

        1.5取最少的木棍

2.背包问题

3.找工作

4.判断是否符合人类正常书写

---

1.斐波那切数列套路

1.1F(N)=F(N-1)+F(N-2)

 

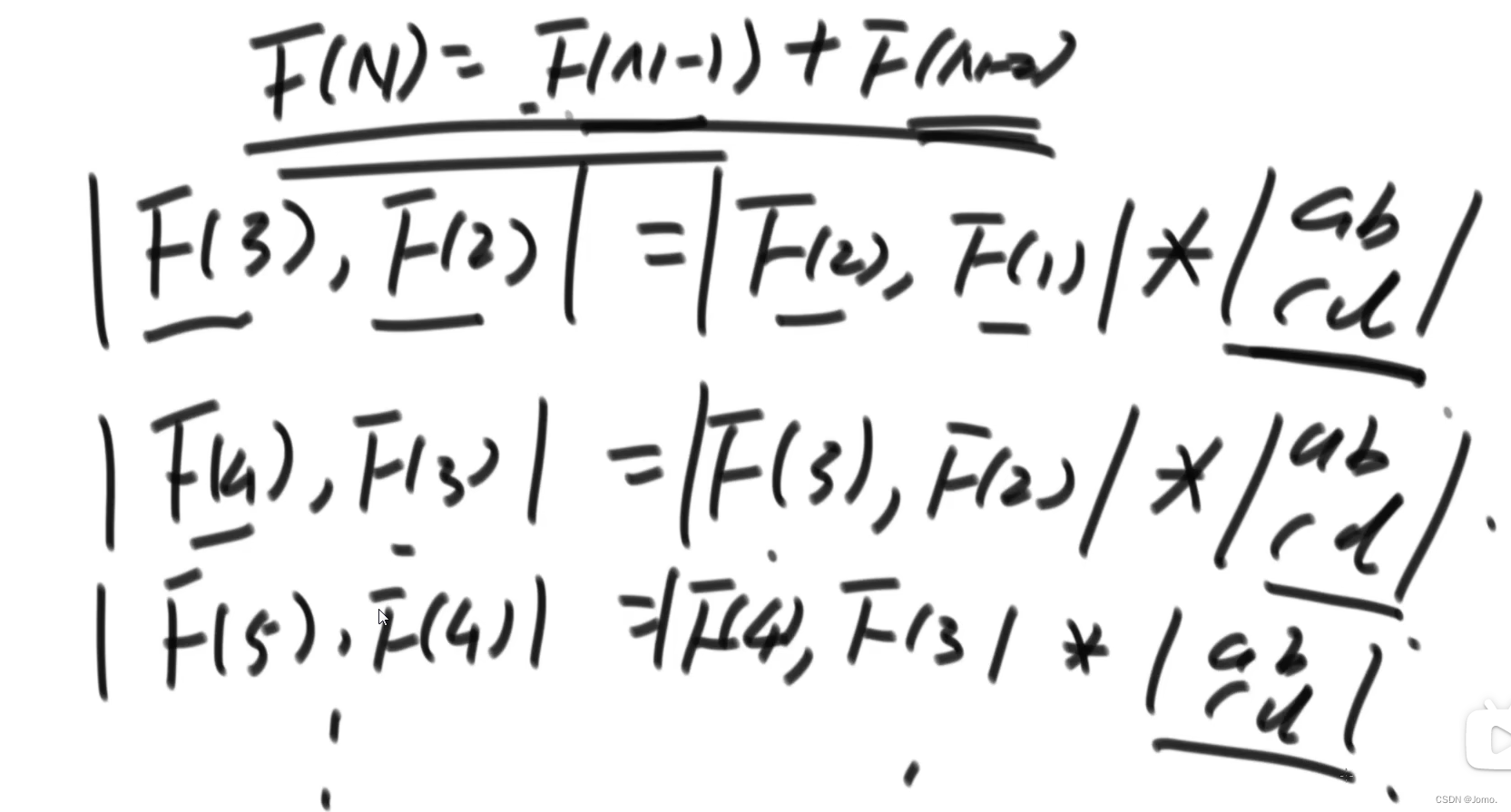
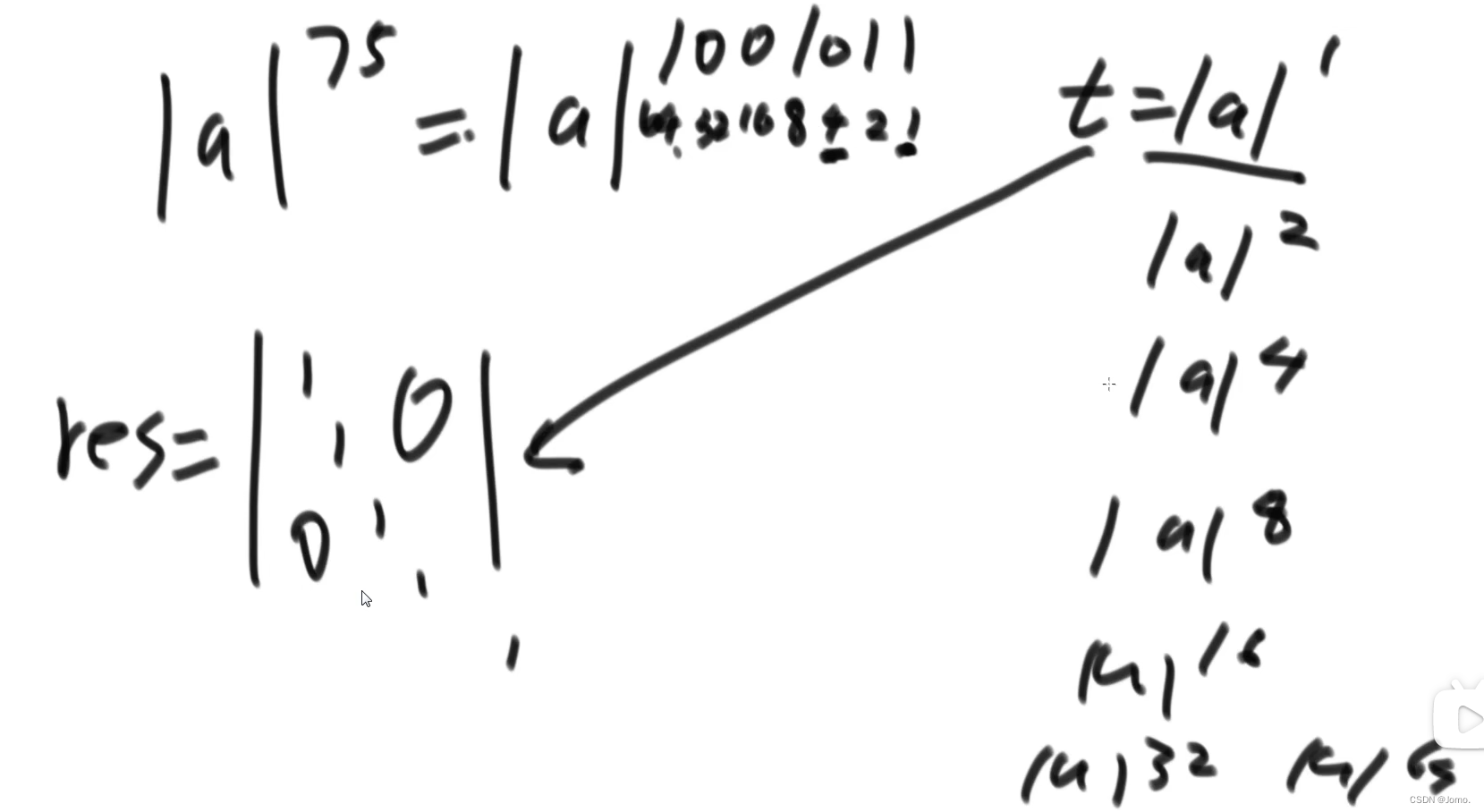
线性代数：
1. 利用初始项可以吧a,b,c,d算出来
2. a=b=c=1,d=0
3. 假设由abcd组成的矩阵为D
4. |F(N),F(N-1)|=|1,1|*D^(n-2)
5. 问题转成如何计算一个矩阵的幂次方
  5.1 先理解O(logn)计算一个数的幂次方
//时间复杂度为O(logn)计算num的n次方
int power(int num, int n) {
	int res = 1;
	int t = num;
	while (n > 0) {//把n看作2进制数，哪一位是1，就让res乘等于对应的10的幂次方
		if ((n & 1) == 1) {//当前位(最低位)是1
			res *= t;
		}
		n >>= 1;
		t *= num;
	}
	return res;
}
  5.2 计算矩阵的幂次方：如上图所示
6.所以完成了O(logn)计算斐波那契数
//返回矩阵m1、m2相乘的结果
vector<vector<int>>muliMatrix(vector<vector<int>>& m1, vector<vector<int>>& m2) {
	vector<vector<int>>res(m1.size(), vector<int>(m2[0].size()));
	for (int i = 0; i < m1.size(); i++) {
		for (int j = 0; j < m2[0].size(); j++) {
			for (int k = 0; k < m2.size(); k++) {
				res[i][j] += m1[i][k] + m2[k][j];
			}
		}
	}
	return res;
}

vector<vector<int>>matrixPower(vector<vector<int>>& m, int p) {
	vector<vector<int>>res(m.size(), vector<int>(m[0].size()));
	for (int i = 0; i < res.size(); i++) {//令矩阵对角线全为1，其他都为0
		res[i][i] = 1;
	}
	vector<vector<int>>t = m;
	for (; p != 0; p >>= 1) {
		if ((p & 1) == 1) {
			res = muliMatrix(res, t);
		}
		t = muliMatrix(t, t);
	}
	return res;
}

//O(logn)计算斐波那切数
int fi(int n) {
	if (n < 1)return 0;
	if (n == 1 || n == 2) return 1;
	vector<vector<int>>base = { {1,1},
													{1,0} };
	vector<vector<int>>res = matrixPower(base, n - 2);
	/*
	| F(N), F(N - 1) |= | 1, 1 | *D ^ (n - 2)
	假设D^(n-2)={{X,Y},{P,Q}}
	X+P=F(N)
	Y+Q=F(N-1)
	*/ 
	return res[0][0] + res[1][0];//X=res[0][0],P=res[1][0]
}

1.2F(N)=3F(N-1)-4F(N-3)+6F(N-5)

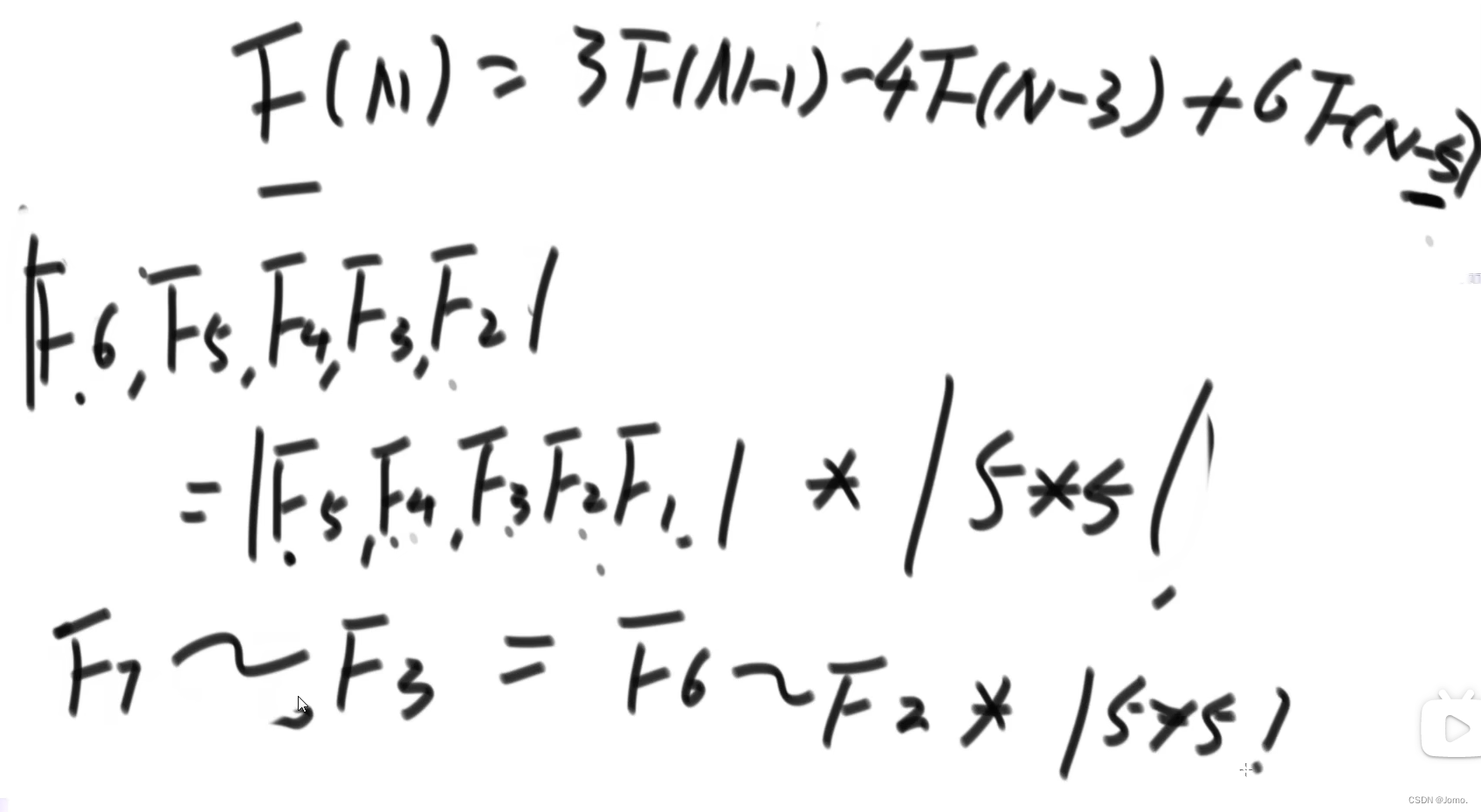
 |5*5|：5*5的矩阵

 1.3生牛问题

一头牛从出生到成熟可生牛的时间为3年，假设第1年只有1头牛，那么第n年总共有几头牛？
PS：牛不会死，一头牛每年只生一只牛
F(N)=F(N-1)+F(N-3)
F(N-1)：前一年留下的牛
F(N-3)：三年前的牛全都成熟后生下的新牛数
所以，利用3阶矩阵解决问题
|F(N),F(N-1),F(N-2)|=|F(3),F(2),F(1)|*D^(n-2)

1.4达标串数量

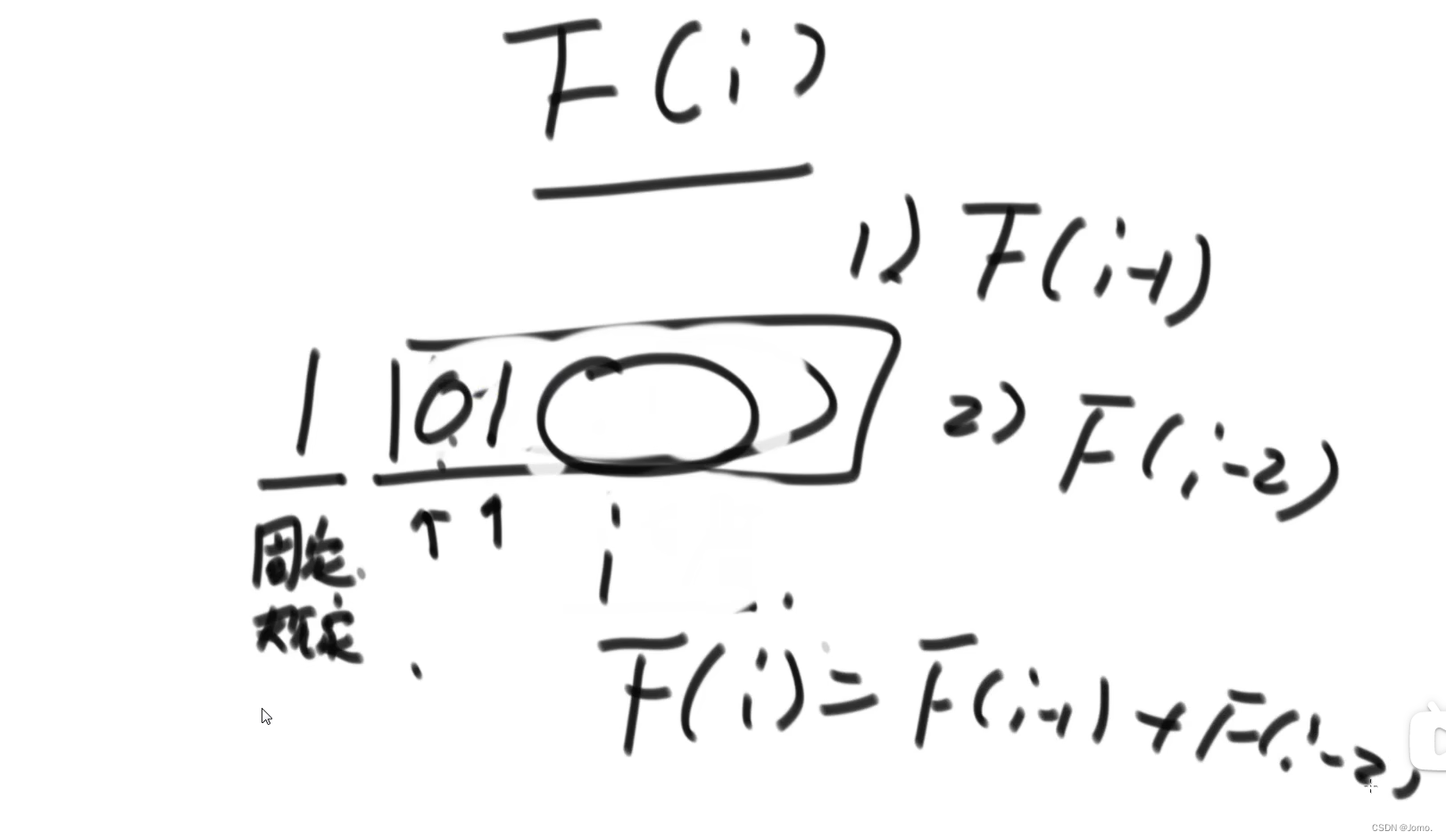
 思路：
    1. 求长度为i的达标串数量
    2. 第0位上的肯定是1，所以看后面i-1位
      2.1 s[1]=1：达标串数量为 F(i-1)
      2.2 s[1]=0，那么s[2]必定是1：达标串数量为 F(i-2)
    3. F(i)=F(i-1)+F(i-2)

 1.5取最少的木棍

 思路：
保留斐波那切数，其他全删去

2.背包问题

 思路：
动态规划二维表：行（各零食体积），列（1~w）
dp[i][j]=dp[i-1][j]+dp[i][j-arr[i]];//不选择i零食的情况+选择i零食的情况

 3.找工作

思路：
    1.创建有序表，难度不同的按难度从小到大，难度相同的为一组，按照报酬从大到小排
    2.同组的只留组长（报酬高的）
    3.把难度提升但是报酬不提高的工作删去
    4.最终只留下难度和报酬单调递增的工作

class Job {
public:
	int money;
	int hard;
	
	Job(int money, int hard) {
		this->money = money;
		this->hard = hard;
	}
};

class JobComparator {
public:
	bool compare(Job o1, Job o2) {
		return o1.hard != o2.hard ? o2.hard - o1.hard : o1.money - o2.money;
	}
};

vector<int>getMoneys(vector<Job>job,vector<int>ability){
	sort(job.begin(), job.end(), JobComparator());
	//难度为key的工作，最优工资是value
	map<int, int>map;
	map[job[0].hard] = job[0].money;
	Job pre = job[0];
	for (int i = 0; i < job.size(); i++) {
		if (job[i].hard != pre.hard && job[i].money > pre.money) {//前者只保留组长，后者删去不保证单调性的工作
			pre = job[i];
			map[job[i].hard] = job[i].money;
		}
	}
	vector<int>ans(ability.size());
	for (int i = 0; i < ability.size(); i++) {
		auto it = map.upper_bound(ability[i]);//找到第一个大于该能力值的工作
		if (it != map.begin()) {
			it--;
			ans[i] = it->second;
		}
		else {//找不到匹配的工作
			ans[i] = 0;
		}
	}
	return ans;
}

 4.判断是否符合人类正常书写

思路：
    1.除了数字之外，只允许出现负号
    2.如果有负号，只会出现在开头，且只出现一次
    3.负号必须跟着数字，且不可以是0
    4.如果开头字符是0，后面不能有其他数字
    5.判断越界：将字符串转成数字，且都转为负数，因为|INT_MIN|-|INT_MAX|=1
    6.定义两个变量：int minq=INT_MIN/10;int minr=INT_MIN%10;用于判断是否越界
    7.if(res<minq||res==minq&&cur<minr)，判断溢出条件