SimpleCG绘图函数(8)--绘制多边形

news2024/11/27 4:28:53

        在这里将展示多边形的绘制，多边形可以绘制从三角形到任意多边形。绘制函数如下所示:

//多边形以一组POINT表示的点坐标数组ptPoints为顶点，nNum表示数组中的点数量
 
//画无填充多边形
void polygon( const POINT *ptPoints, int nNum );
 
//画无边框填充多边形
void solidpolygon( const POINT *ptPoints, int nNum );
 
//画填充多边形
void fillpolygon( const POINT *ptPoints, int nNum );
 
//清空多边形
void clearpolygon( const POINT *ptPoints, int nNum );

多边形是由n个点连接的边围成的图形,所以我们只需定义一个点的数组,及数组元素个数即可确定这个多边形。所以我们看到多边形绘制函数只有两个参数，分别是点数组的指针const POINT *ptPoints,，及点的个数int nNum。

        我们先绘制个简单三角形，看看函数如何调用。只需给出三个点坐标，代码如下：

POINT pt[]={{20,20},{380,20},{240,350}};
setfillcolor(RGB(200,200,255));
fillpolygon(pt,sizeof(pt)/sizeof(pt[0]));

绘制图形如下：

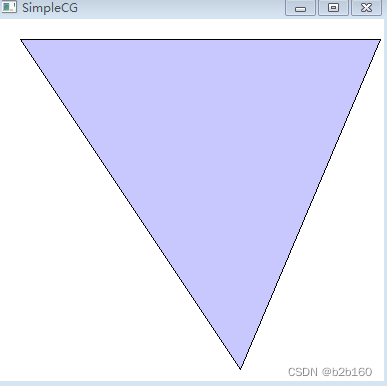
        通过给定点的数组，及点的数量即可绘制出对应的多边形，非常简单。不过这是针对顺序点连接的多边形。如果是连接线段相互穿插的话，则情况比较复杂。例如如下代码，点与点在图形间穿插。

POINT pt[]={{10,50},{300,50},{300,300},{10,300},{10,50},{50,300},{100,50},{150,300},{200,50},{250,300},{300,50}};
setfillcolor(RGB(200,180,220));
fillpolygon(pt,sizeof(pt)/sizeof(pt[0]));

绘制的图形如下所示：

其中数字标明了绘制点的顺序，我们看到整个图形用的填充色是一种，而且前面5个点已经围了一个矩形，但发现有些地方填充了，有些地方却没填充。这是因为默认的多边形填充模式中， 采用的是间隔填充，关于填充模式后面进行进一步介绍。默认模式中，从左往右看绿色箭头，察看穿过该绿色线的线段条数，奇数条数开始填充，偶数条数结束填充。例如看第一个浅紫色色块，首先穿过4--5线段时属于奇数次开始填充紫色，穿过5--6线段时，属于偶数次结束填充紫色，后面没填充就一块白色，穿过6--7时又属于奇数次又开始填充紫色，穿过7--8时属于偶数次，结束填充紫色。以此类推。。。除非对填充模式比较了解，并且确实需要这样间隔填充，否则还是不建议使用这种穿插的点来绘制

        下面通过绘制正多边形和星形来展示多边形绘制，正多边形代码如下：

// Polygon.cpp : 定义控制台应用程序的入口点。
//

#include "../import/include/CGBoard.h"
#include "math.h"
#ifdef _DEBUG
#pragma comment(lib,"../import/lib/SimpleCG_MDd.lib")
#else
#pragma comment(lib,"../import/lib/SimpleCG_MD.lib")
#endif

#define ADDCOLOR(x,y) ((x+y)>255?255:(x+y))
#define SUBCOLOR(x,y) ((x-y)<0?0:(x-y))

int g_nWidth = 400;		//画面宽度
int g_nHeight= 400;		//画面高度
//绘制任意正多边形
void RegularPolygon( int nCount, int nCenterX, int nCenterY, int nRatio, float fStartAngle)
{
	POINT *pts = (POINT *)malloc(sizeof(POINT)*nCount);
	if(NULL==pts)
		return;
	float fDelta = 2*C_PI/nCount;
	int i=0;
	for(i=0;i<nCount;++i)
	{
		pts[i].x=nCenterX + nRatio * cos(fStartAngle) + 0.5;
		pts[i].y=nCenterY - nRatio * sin(fStartAngle) + 0.5;
		fStartAngle += fDelta;
	}
	fillpolygon(pts,nCount);
	free(pts);
}

void DrawProcess()
{

	int i=0;
	for(i=0;i<12;++i)
	{
		setfillcolor(RGB(rand()%255,rand()%255,rand()%255));
		RegularPolygon(i+3, (i%4)*100 + 100, i/4*100 + 100,40,C_PI/2);
	}
}
int _tmain(int argc, _TCHAR* argv[])
{
	//初始化
	if( !ShowingBoard(g_nWidth,g_nHeight, DrawProcess))
		return 1;
	//关闭图库
	CloseBoard();
	return 0;
}

运行效果如下图

定义了函数RegularPolygon，可以绘制任意多边形。演示代码绘制了从正三角形开始，一直到正14边形，不过越到后面已经越接近圆了。 

        另外再展示一下星形绘制，以下代码同样显示了多边形的强大功能。

// Polygon.cpp : 定义控制台应用程序的入口点。
//

#include "../import/include/CGBoard.h"
#include "math.h"
#ifdef _DEBUG
#pragma comment(lib,"../import/lib/SimpleCG_MDd.lib")
#else
#pragma comment(lib,"../import/lib/SimpleCG_MD.lib")
#endif

#define ADDCOLOR(x,y) ((x+y)>255?255:(x+y))
#define SUBCOLOR(x,y) ((x-y)<0?0:(x-y))

int g_nWidth = 400;		//画面宽度
int g_nHeight= 400;		//画面高度

void Star(int nCount, int nCenterX, int nCenterY, int nRatioInner, int nRatioOuter, float fStartAngle)
{
	POINT *pts = (POINT *)malloc(sizeof(POINT)*nCount*2);
	if(NULL==pts)
		return;
	float fDelta = 2*C_PI/nCount;
	int i=0;
	for(i=0;i<nCount;++i)
	{
		pts[2*i].x=nCenterX + nRatioOuter * cos(fStartAngle) + 0.5;
		pts[2*i].y=nCenterY - nRatioOuter * sin(fStartAngle) + 0.5;
		pts[2*i+1].x=nCenterX + nRatioInner * cos(fStartAngle+fDelta/2) + 0.5;
		pts[2*i+1].y=nCenterY - nRatioInner * sin(fStartAngle+fDelta/2) + 0.5;
		fStartAngle += fDelta;
	}

	fillpolygon(pts,nCount*2);
	free(pts);
}

void DrawProcess()
{

	int i=0;
	for(i=0;i<12;++i)
	{
		setfillcolor(RGB(rand()%255,rand()%255,rand()%255));
		Star(i+3, (i%4)*100 + 100, i/4*100 + 100,20,40,C_PI/2);
	}
}
int _tmain(int argc, _TCHAR* argv[])
{
	//初始化
	if( !ShowingBoard(g_nWidth,g_nHeight, DrawProcess))
		return 1;
	//关闭图库
	CloseBoard();
	return 0;
}

代码只是用Star函数替换了正多边形函数，其他代码差不多一致。运行效果如图：

正多边形函数可以绘制一切线段围成的图形，从上面程序已经看出他甚至能模拟出圆形，所以可以说只要愿意，几乎可以绘制所有图形。

下面我们来绘制一个大宝剑来进一步 学习该函数的应用。代码如下：

// Polygon.cpp : 定义控制台应用程序的入口点。
//

#include "../import/include/CGBoard.h"
#include "math.h"
#ifdef _DEBUG
#pragma comment(lib,"../import/lib/SimpleCG_MDd.lib")
#else
#pragma comment(lib,"../import/lib/SimpleCG_MD.lib")
#endif

#define ADDCOLOR(x,y) ((x+y)>255?255:(x+y))
#define SUBCOLOR(x,y) ((x-y)<0?0:(x-y))

int g_nWidth = 400;		//画面宽度
int g_nHeight= 600;		//画面高度

void Sward1(int nX, int nY)
{
	int i=0;
	//剑身
	POINT pt1[]={{nX,nY},{nX-20,nY+30},{nX-20,nY+400},{nX+20,nY+400},{nX+20,nY+30},{nX,nY}};
	setfillcolor(RGB(232,235,250));
	fillpolygon(pt1,sizeof(pt1)/sizeof(pt1[0]));
	POINT pt2[]={{nX,nY},{nX-20,nY+30},{nX-20,nY+400},{nX,nY+400},{nX,nY}};
	setfillcolor(RGB(160,160,220));
	fillpolygon(pt2,sizeof(pt2)/sizeof(pt2[0]));
	POINT pt3[]={{nX,nY+20},{nX-4,45},{nX-4,nY+399},{nX+4,nY+399},{nX+4,45},{nX,nY+20}};
	setfillcolor(RGB(225,225,255));
	solidpolygon(pt3,sizeof(pt3)/sizeof(pt3[0]));
	POINT pt4[]={{nX,nY+20},{nX,nY+399},{nX+4,nY+399},{nX+4,45},{nX,nY+20}};
	setfillcolor(RGB(100,100,160));
	fillpolygon(pt4,sizeof(pt4)/sizeof(pt4[0]));

	//剑柄
	{
		POINT pt[]={{nX-35,nY+420},{nX-30,nY+400},{nX+30,nY+400},{nX+35,nY+420},{nX+20,nY+410},{nX-20,nY+410}};
		setfillcolor(RGB(237,170,24));
		fillpolygon(pt,sizeof(pt)/sizeof(pt[0]));
	}
	{
		POINT pt[]={{nX-30,nY+405},{nX-30,nY+402},{nX+30,nY+402},{nX+34,nY+419},{nX+25,nY+405},{nX-30,nY+405}};
		setfillcolor(RGB(255,234,134));
		solidpolygon(pt,sizeof(pt)/sizeof(pt[0]));
	}
	{
		POINT pt[]={{nX-10,nY+410},{nX-10,nY+490},{nX+10,nY+490},{nX+10,nY+410}};
		setfillcolor(RGB(120,80,0));
		fillpolygon(pt,sizeof(pt)/sizeof(pt[0]));
	}
	
	COLORREF nColor = RGB(120,80,0);
	for(i=nX-2;i<nX+10;++i)
	{
		int r=ADDCOLOR(GetRValue(nColor),8);
		int g=ADDCOLOR(GetGValue(nColor),8);
		int b=ADDCOLOR(GetBValue(nColor),8);
		nColor = RGB(r,g,b);
		setlinecolor(nColor);
		line(i,nY+411,i,nY+490);
	}
	{
		setlinecolor(0);
		POINT pt[]={{nX,nY+470},{nX-15,nY+490},{nX,nY+530},{nX+15,nY+490}};
		setfillcolor(RGB(237,170,24));
		fillpolygon(pt,sizeof(pt)/sizeof(pt[0]));
	}
	{
		POINT pt[]={{nX-14,nY+490},{nX,nY+529},{nX,nY+490}};
		setfillcolor(RGB(187,120,0));
		solidpolygon(pt,sizeof(pt)/sizeof(pt[0]));
	}
	{
		POINT pt[]={{nX+14,nY+490},{nX,nY+471},{nX,nY+490}};
		setfillcolor(RGB(255,220,74));
		solidpolygon(pt,sizeof(pt)/sizeof(pt[0]));
	}
	//宝石
	{
		setlinecolor(RGB(87,20,0));
		POINT pt[]={{nX,nY+480},{nX-5,nY+490},{nX,nY+500},{nX+5,nY+490}};
		setfillcolor(RGB(0,200,200));
		fillpolygon(pt,sizeof(pt)/sizeof(pt[0]));
	}
	{
		POINT pt[]={{nX-5,nY+490},{nX,nY+500},{nX,nY+490}};
		setfillcolor(RGB(0,120,100));
		solidpolygon(pt,sizeof(pt)/sizeof(pt[0]));
	}
	{
		POINT pt[]={{nX,nY+480},{nX,nY+490},{nX+5,nY+490}};
		setfillcolor(RGB(150,255,250));
		solidpolygon(pt,sizeof(pt)/sizeof(pt[0]));
	}

}
void Sward2(int nX, int nY)
{
	int i=0;
	//剑身
	POINT pt1[]={{nX,nY},{nX-20,nY+30},{nX-20,nY+400},{nX+20,nY+400},{nX+20,nY+30},{nX,nY}};
	setfillcolor(RGB(177,250,200));
	fillpolygon(pt1,sizeof(pt1)/sizeof(pt1[0]));
	POINT pt2[]={{nX,nY},{nX-20,nY+30},{nX-20,nY+400},{nX,nY+400},{nX,nY}};
	setfillcolor(RGB(50,180,130));
	fillpolygon(pt2,sizeof(pt2)/sizeof(pt2[0]));
	POINT pt3[]={{nX,nY+20},{nX-4,45},{nX-4,nY+399},{nX+4,nY+399},{nX+4,45},{nX,nY+20}};
	setfillcolor(RGB(177,250,200));
	solidpolygon(pt3,sizeof(pt3)/sizeof(pt3[0]));
	POINT pt4[]={{nX,nY+20},{nX,nY+399},{nX+4,nY+399},{nX+4,45},{nX,nY+20}};
	setfillcolor(RGB(0,180,130));
	fillpolygon(pt4,sizeof(pt4)/sizeof(pt4[0]));

	//剑柄
	{
		POINT pt[]={{nX-35,nY+420},{nX-30,nY+400},{nX+30,nY+400},{nX+35,nY+420},{nX+20,nY+410},{nX-20,nY+410}};
		setfillcolor(RGB(237,170,24));
		fillpolygon(pt,sizeof(pt)/sizeof(pt[0]));
	}
	{
		POINT pt[]={{nX-30,nY+405},{nX-30,nY+402},{nX+30,nY+402},{nX+34,nY+419},{nX+25,nY+405},{nX-30,nY+405}};
		setfillcolor(RGB(255,234,134));
		solidpolygon(pt,sizeof(pt)/sizeof(pt[0]));
	}
	{
		POINT pt[]={{nX-10,nY+410},{nX-10,nY+490},{nX+10,nY+490},{nX+10,nY+410}};
		setfillcolor(RGB(120,80,0));
		fillpolygon(pt,sizeof(pt)/sizeof(pt[0]));
	}
	
	COLORREF nColor = RGB(120,80,0);
	for(i=nX-2;i<nX+10;++i)
	{
		int r=ADDCOLOR(GetRValue(nColor),8);
		int g=ADDCOLOR(GetGValue(nColor),8);
		int b=ADDCOLOR(GetBValue(nColor),8);
		nColor = RGB(r,g,b);
		setlinecolor(nColor);
		line(i,nY+411,i,nY+490);
	}
	{
		setlinecolor(0);
		POINT pt[]={{nX,nY+470},{nX-15,nY+490},{nX,nY+530},{nX+15,nY+490}};
		setfillcolor(RGB(237,170,24));
		fillpolygon(pt,sizeof(pt)/sizeof(pt[0]));
	}
	{
		POINT pt[]={{nX-14,nY+490},{nX,nY+529},{nX,nY+490}};
		setfillcolor(RGB(187,120,0));
		solidpolygon(pt,sizeof(pt)/sizeof(pt[0]));
	}
	{
		POINT pt[]={{nX+14,nY+490},{nX,nY+471},{nX,nY+490}};
		setfillcolor(RGB(255,220,74));
		solidpolygon(pt,sizeof(pt)/sizeof(pt[0]));
	}
	//宝石
	{
		setlinecolor(RGB(87,20,0));
		POINT pt[]={{nX,nY+480},{nX-5,nY+490},{nX,nY+500},{nX+5,nY+490}};
		setfillcolor(RGB(160,160,220));
		fillpolygon(pt,sizeof(pt)/sizeof(pt[0]));
	}
	{
		POINT pt[]={{nX-5,nY+490},{nX,nY+500},{nX,nY+490}};
		setfillcolor(RGB(110,110,170));
		solidpolygon(pt,sizeof(pt)/sizeof(pt[0]));
	}
	{
		POINT pt[]={{nX,nY+480},{nX,nY+490},{nX+5,nY+490}};
		setfillcolor(RGB(230,230,255));
		solidpolygon(pt,sizeof(pt)/sizeof(pt[0]));
	}

}
void DrawProcess()
{
	
	Sward1(100,20);
	Sward2(250,20);

}
int _tmain(int argc, _TCHAR* argv[])
{
	//初始化
	if( !ShowingBoard(g_nWidth,g_nHeight, DrawProcess))
		return 1;
	//关闭图库
	CloseBoard();
	return 0;
}

运行效果如下图所示：

 程序绘制了紫青双剑，几乎所有元素的绘制仅仅使用了多边形绘制函数。所以只要掌握好了多边形绘制，许多复杂图形都能够轻松绘制出来。

好了，以上就介绍完了多边形的绘制方法。还是那句话，多多上手练习，就能熟练运用到实际绘制项目中去了。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/647146.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Android进阶 四大组件的工作过程（三）：广播的注册，发送和接收过程

Android进阶 四大组件的工作过程（三）：广播的注册，发送和接收过程

Android进阶 四大组件的工作过程&#xff08;三&#xff09;&#xff1a;广播的注册&#xff0c;发送和接收过程 导语 本篇文章是介绍四大组件工作过程的第三篇文章&#xff0c;在前两篇文章里我们已经介绍了Activity和Service的工作流程。而本篇文章&#xff0c;我们将介绍广…
阅读更多...
第七十四天学习记录：高等数学：不定积分（宋浩板书）

第七十四天学习记录：高等数学：不定积分（宋浩板书）

给定一个函数f(x)&#xff0c;如果存在一个函数F(x)&#xff0c;满足F’(x)f(x)&#xff0c;则称F(x)是f(x)的一个原函数。我们通常用∫f(x)dx表示f(x)的不定积分&#xff0c;它表示的是所有原函数的集合&#xff0c;也就是说&#xff0c;∫f(x)dx就是f(x)的原函数集合。 不定…
阅读更多...
Docker安装wordpress并配置数据库(超详细版)

Docker安装wordpress并配置数据库(超详细版)

Docker在线拉取安装wordpress并配置数据库 一、拉取wordpress镜像(默认最新)二、启动wordpress容器三、查看容器状态四、安装wordpress博客程序 如果您已经在 Docker 容器中分别安装了 WordPress 和 MySQL&#xff0c;并且想要让它们链接起来&#xff0c;可以按照以下步骤进行操…
阅读更多...
什么是三极管的截止饱和放大

什么是三极管的截止饱和放大

三极管可以工作在三个状态&#xff0c;分别是截止状态&#xff0c;饱和状态和放大状态。 当三级管BE之间的电压小于等于BE间的开启电压UON&#xff0c;并且CE间电压>BE间电压时 &#xff0c;三极管处于截止状态&#xff0c;一般硅管在0.7V左右&#xff0c;锗管在0.3V左右。…
阅读更多...
数据库第三章（SQL）

数据库第三章（SQL）

目录 1.SQL语言 索引 1.SQL语言 sql语言是个非过程性语言 sql的特点 1.综合统一&#xff0c;把增删查改都统一了起来 2.高度非过程化&#xff0c;不关心过程 3.面向集合的操作方式 sql基本语法 drop是删除表 delete是删除表的某个元组 安全方面&#xff1a;grant授权 revo…
阅读更多...
Java实训日志05

Java实训日志05

文章目录 八、项目开发实现步骤&#xff08;七&#xff09;创建数据访问接口实现类1、创建学校数据访问接口实现类&#xff08;1&#xff09;编写按标识符查询学校记录方法&#xff08;2&#xff09;编写更新学校记录方法 1_、测试学校数据访问接口实现类&#xff08;1&#xf…
阅读更多...
在Nginx服务器如何安装SSL证书

在Nginx服务器如何安装SSL证书

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 文章目录 前言提示&#xff1a;我用的是阿里云的产品&#xff0c;就以阿里云进行的&#xff1a; 一、下载SSL证书二、安装SSL证书 前言 提示&#xff1a;我用的是阿里云的产…
阅读更多...
多元回归预测 | Matlab遗传算法(GA)优化核极限学习机回归，GA-KELM回归预测，多变量输入模型

多元回归预测 | Matlab遗传算法(GA)优化核极限学习机回归，GA-KELM回归预测，多变量输入模型

文章目录 效果一览文章概述部分源码参考资料效果一览 文章概述 多元回归预测 | Matlab遗传算法(GA)优化核极限学习机回归，GA-KELM回归预测，多变量输入模型 评价指标包括:MAE、RMSE和R2等，代码质量极高，方便学习和替换数据。要求2018版本及以上。 部分源码 %% 清空环境变量…
阅读更多...
设计模式(十六)：行为型之责任链模式

设计模式(十六)：行为型之责任链模式

设计模式系列文章 设计模式(一)&#xff1a;创建型之单例模式 设计模式(二、三)&#xff1a;创建型之工厂方法和抽象工厂模式 设计模式(四)&#xff1a;创建型之原型模式 设计模式(五)&#xff1a;创建型之建造者模式 设计模式(六)&#xff1a;结构型之代理模式 设计模式…
阅读更多...
2.链表的实现：带哨兵

2.链表的实现：带哨兵

1.带哨兵的单链表的定义 /*** 单向链表----带哨兵*/ public class SinglyLinked {/*** 节点类* 数据域和地址域*/private static class Node {int value; //值Node next; // 指向下一个节点public Node() {}public Node(int value, Node next) {this.value value;this.next …
阅读更多...
【linux】在Ubuntu20.04下录制屏幕为视频，并制作成gif动态图片

【linux】在Ubuntu20.04下录制屏幕为视频，并制作成gif动态图片

1、下载软件 录制屏幕软件 sudo apt install simplescreenrecorder视频转图片软件 sudo apt install mplayer图片合成gif动态图片 sudo apt install imagemagick2、录制屏幕 1）运行命令 simplescreenrecorder2）设置：区域、帧率 选择录制的区域; 设置帧率为10（或者更小…
阅读更多...
3.vue 指令

3.vue 指令

3.10 v-text和v-html 更新 DOM 对象的 innerText / innerHTML 语法: v-text"vue数据变量" v-html"vue数据变量" 注意: 会覆盖插值表达式 v-text 把值当成普通字符串显示 v-html 把值当做 html 解析 <template><div><p v-text"str…
阅读更多...
关于自动化测试框架pytest的Fixture固件

关于自动化测试框架pytest的Fixture固件

这篇文章主要介绍了关于自动化测试框架pytest的Fixture固件,Fixture它其实就是一些函数,会在执行测试方法/测试函数前后加载运行它们,需要的朋友可以参考下 目录 什么是固件定义方式调用方式使用fixture传递测试数据conftest.py作用域总结 什么是固件 Fixture 翻译成中文即是固…
阅读更多...
无效目标发行版问题解决记录

无效目标发行版问题解决记录

​ SpringMVC之‘无效目标发行版’ 问题&#xff1a;上死亡截图 问题解决思路&#xff1a;这是由于JDK版本不匹配导致的错误。 首先说一下问题的关键所在&#xff0c;然后再细说解决步骤&#xff1a; 遇到这个问题的朋友大概率都是在写Spring项目时遇到的&#xff0c;这就需要M…
阅读更多...
H3C-HCL模拟器常用命令及其操作演示

H3C-HCL模拟器常用命令及其操作演示

一、实验拓扑图 二、实验设备 设备1&#xff1a;路由器"MSR36-20"&#xff1b; 设备2&#xff1a;真机&#xff1b; 三、常用命令 1&#xff09;进入用户视图&#xff1a;启动默认就是用户视图 "< >" 2&#xff09;进入系统视图&#xff1a;"…
阅读更多...
揭示GPT Tokenizer的工作原理

揭示GPT Tokenizer的工作原理

在GPT模型中&#xff0c;tokenization&#xff08;词元化&#xff09;指的是将用户输入的文本分割成token&#xff08;词元&#xff09;的过程&#xff0c;以让GPT能更好地理解输入文本的词义、句法和语义&#xff0c;以及生成更连贯的输出内容。这是非常重要的预处理操作&…
阅读更多...
C++AVL树

C++AVL树

目录&#xff1a; AVL树的概念AVL树节点的定义更新平衡因子 AVL树的旋转AVL树的验证AVL的整体实现 AVL树的删除AVL树的性能 总结 AVL树的概念 AVL树&#xff1a;二叉搜索树虽可以缩短查找的效率&#xff0c;但如果数据有序或接近有序二叉搜索树将退化为单支树&#xff0c;查找…
阅读更多...
CAPL硬件控制课程，物理故障注入自动化以及程控电源

CAPL硬件控制课程，物理故障注入自动化以及程控电源

&#x1f4d9; CAN/LIN总线物理故障注入&#xff0c;自动化解决方案 车载网络通讯的健壮性和故障恢复能力至关重要&#xff0c;所以我们需要对控制器进行各种物理容错测试&#xff0c;常规情况下我们需要注入如下8种物理故障注入&#xff1a;CANH断路&#xff0c;CANL断路,CANH…
阅读更多...
Redux的基础操作和思想

Redux的基础操作和思想

什么是Redux? Redux是JavaScript应用的状态容器&#xff0c;提供可预测的状态管理! Redux除了和React一起用外&#xff0c;还支持其它框架;它体小精悍(只有2kB&#xff0c; 包括依赖)&#xff0c;却有很强大的插件扩展生态! Redux提供的模式和工具使您更容易理解应用程序中的…
阅读更多...
管理类联考——英语——趣味篇——完型填空

管理类联考——英语——趣味篇——完型填空

完型填空解题秘籍 一、答案分配规律 历年完型答案统计 A B C D 2010 DCBAA/BDCBA/CDDAC/BDCAB 5 5 5 5 2011 ACBDD/BACCB/DBACA/ADACD 6 4 5 5 2012 BBAAC/DAACB/DBCDD/ACCBD 5 5 5 5 2013 ADBDC/BBDBA/ADCCC/CABAD 5 5 5 5 2014 BACAD/ACCDB/ABCDB/DADCB 5 5 5 5 2015 CDC…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023