一、执行上下文

🍟🍟🍟是一种对js代码执行环境的抽象概念 只要有js代码运行，一定是运行在执行上下文中

执行上下文的类型分为三种：

全局执行上下文：只有一个，浏览器中的全局对象就是 window对象，this 指向这个全局对象
函数执行上下文：存在无数个，只有在函数被调用的时候才会被创建，每次调用函数都会创建一个新的执行上下文
Eval 函数执行上下文：指的是运行在 eval 函数中的代码，很少用而且不建议使用

下面给出全局上下文和函数上下文的例子：

在这里插入图片描述
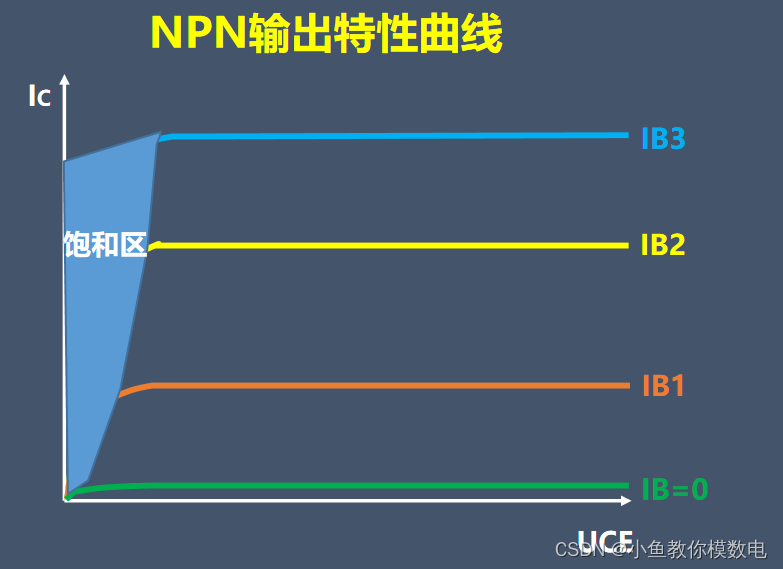
紫色框住的部分为全局上下文，蓝色和橘色框起来的是不同的函数上下文。只有全局上下文（的变量）能被其他任何上下文访问

可以有任意多个函数上下文，每次调用函数创建一个新的上下文，会创建一个私有作用域，函数内部声明的任何变量都不能在当前函数作用域外部直接访问

二、生命周期

🍔🍔🍔执行上下文的生命周期包括三个阶段：创建阶段 → 执行阶段 → 回收阶段。

创建阶段

创建阶段即当函数被调用，但未执行任何其内部代码之前

创建阶段做了三件事

确定 this 的值，也被称为 This Binding
LexicalEnvironment（词法环境）组件被创建
VariableEnvironment（变量环境）组件被创建

伪代码

ExecutionContext = {  
  ThisBinding = <this value>,     // 确定this 
  LexicalEnvironment = { ... },   // 词法环境
  VariableEnvironment = { ... },  // 变量环境
}

This Binding

确定this的值我们前面讲到，this的值是在执行的时候才能确认，定义的时候不能确认

词法环境

全局环境：是一个没有外部环境的词法环境，其外部环境引用为null，有一个全局对象，this 的值指向这个全局对象
函数环境：用户在函数中定义的变量被存储在环境记录中，包含了arguments 对象，外部环境的引用可以是全局环境，也可以是包含内部函数的外部函数环境

伪代码

GlobalExectionContext = { //全局执行上下文
	LexicalEnvironment:{//词法环境
		EnvironmentRecord:{ //环境记录
			Type:"Object", // 全局环境
			outer:<null>  // 对外部环境的引用
		}
	}
}
FunctionExectionContext = { // 函数执行上下文
  LexicalEnvironment: {     // 词法环境
    EnvironmentRecord: {    // 环境记录
      Type: "Declarative",      // 函数环境
      // 标识符绑定在这里      // 对外部环境的引用
      outer: <Global or outer function environment reference>  
  }  
}

变量环境

变量环境也是一个词法环境，因此它具有上面定义的词法环境的所有属性

在 ES6 中，词法环境和变量环境的区别在于前者用于存储函数声明和变量（ let 和 const ）绑定，而后者仅用于存储变量（ var ）绑定

let和const定义的变量，在创建阶段没有被赋值，但var声明的变量从在创建阶段被赋值为undefined

创建阶段，会在代码中扫描变量和函数声明，然后将函数声明存储在环境中

但变量会被初始化为undefined(var声明的情况下)和保持uninitialized(未初始化状态)(使用let和const声明的情况下)

这就是变量提升的实际原因

执行阶段

在这阶段，执行变量赋值、代码执行

如果 Javascript 引擎在源代码中声明的实际位置找不到变量的值，那么将为其分配 undefined 值

回收阶段

执行上下文出栈等待虚拟机回收执行上下文

二、执行栈

🌭🌭🌭概念抽象的不行，摸不着，看不见，特点是后进先出，用于存储在代码执行期间创建的所有执行上下文

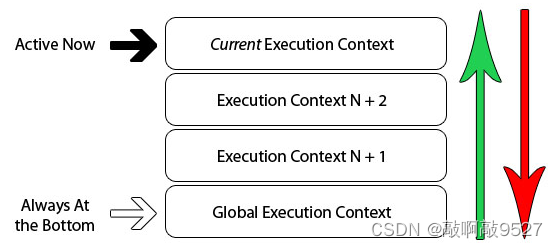
在这里插入图片描述
当引擎执行首行代码时，此时内部会创建一个全局执行上下文而后将这个无中生有的东西压进执行栈中

当遇见一个函数的时候，又会创建对应的函数执行上下文，用来记录，压进执行栈中

执行栈在上面的上下文，会先执行，当执行结束后，就会被弹出，此时一个帮手控制流程到达执行栈的下一个执行上下文

例如

let a = 'Hello World!';
function first() {
  console.log('Inside first function');
  second();
  console.log('Again inside first function');
}
function second() {
  console.log('Inside second function');
}
first();
console.log('Inside Global Execution Context');