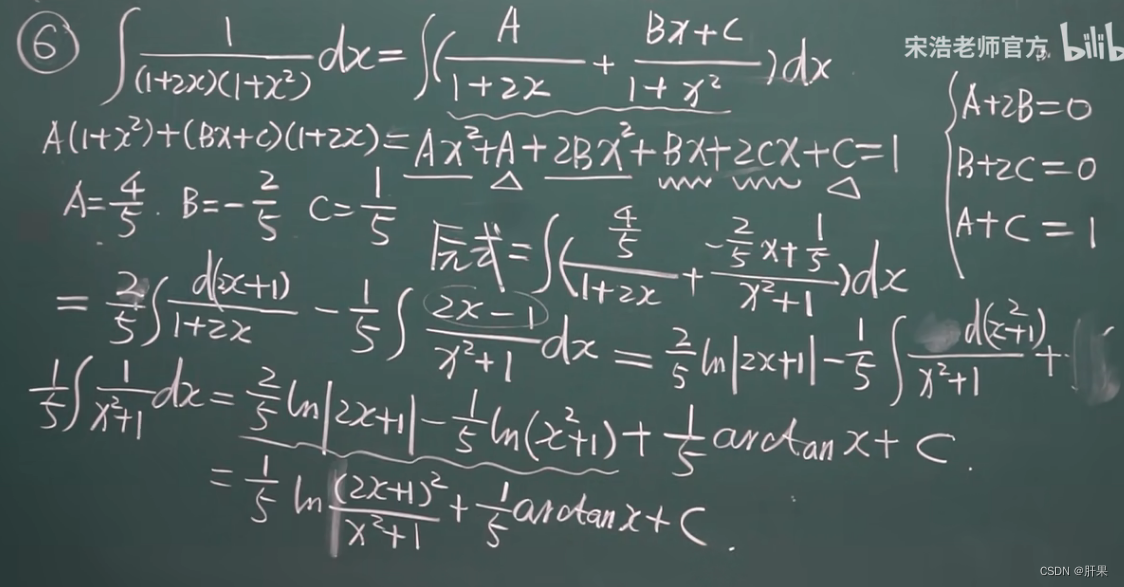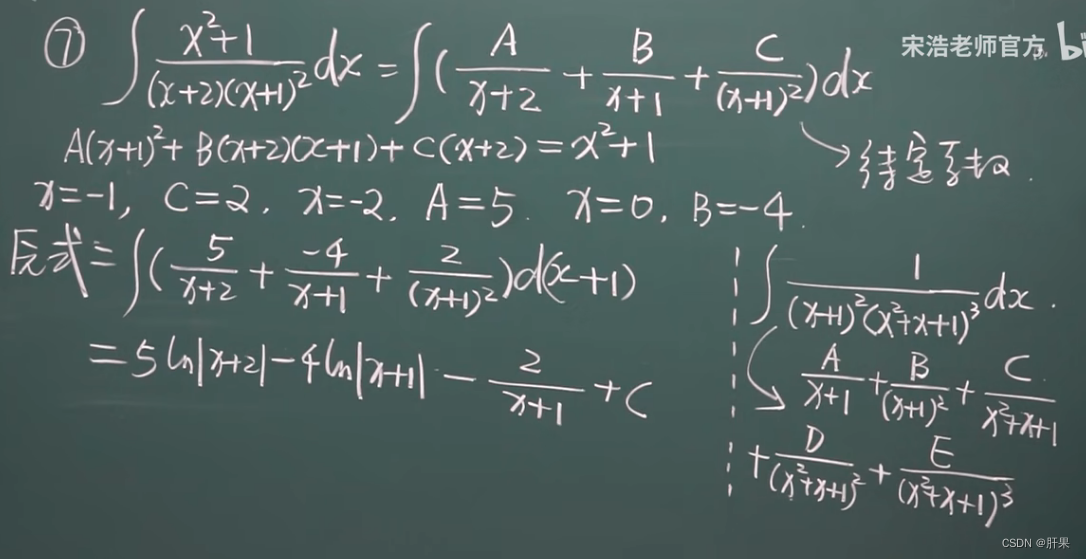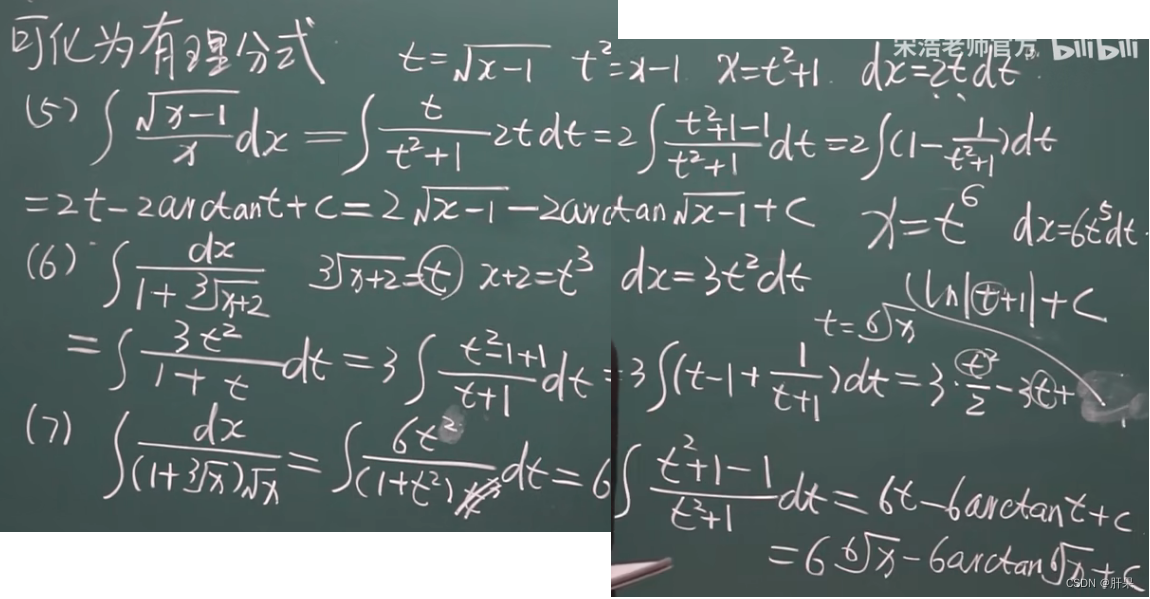给定一个函数f(x),如果存在一个函数F(x),满足F’(x)=f(x),则称F(x)是f(x)的一个原函数。我们通常用∫f(x)dx表示f(x)的不定积分,它表示的是所有原函数的集合,也就是说,∫f(x)dx就是f(x)的原函数集合。
不定积分的主要应用是解决函数的定积分问题。定积分就是对给定区间上的函数进行积分求值。如果我们能求出函数的原函数,那么就可以方便地解决定积分问题。此外,不定积分在微积分、物理学、工程学等方面都有广泛的应用。

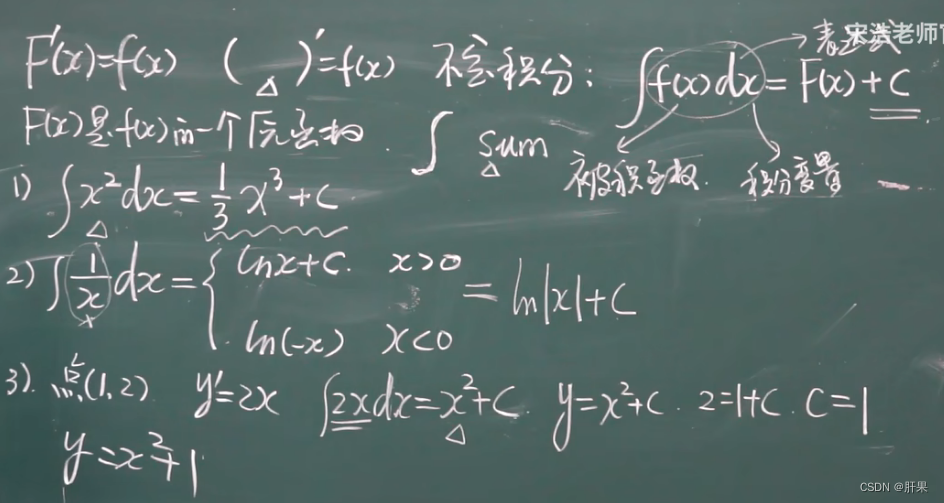

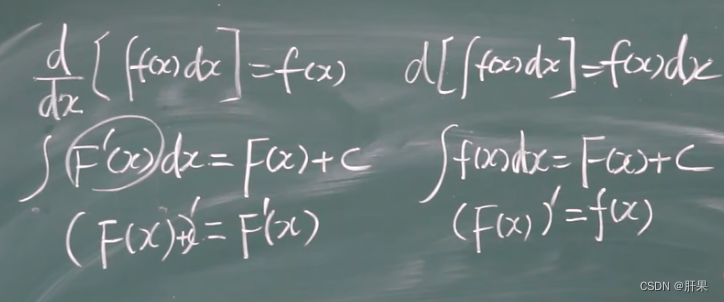

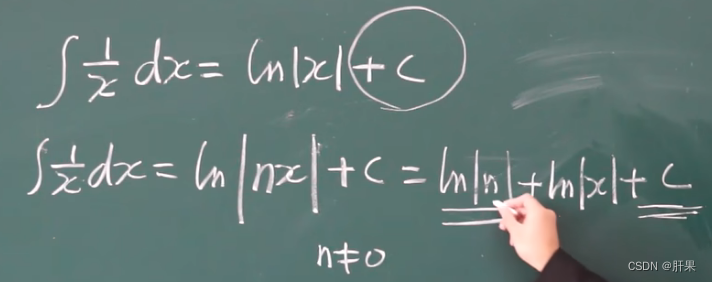


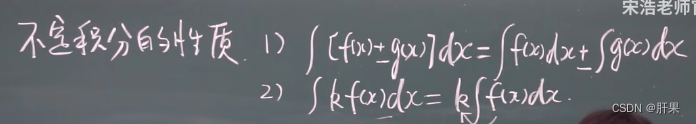
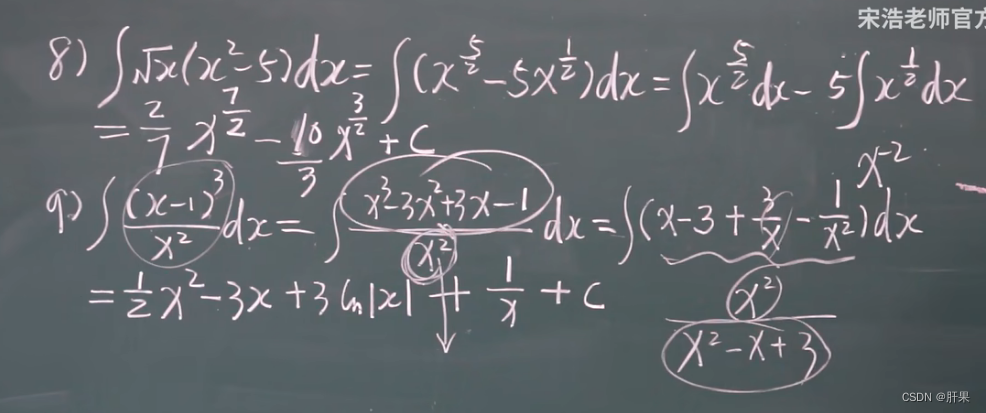
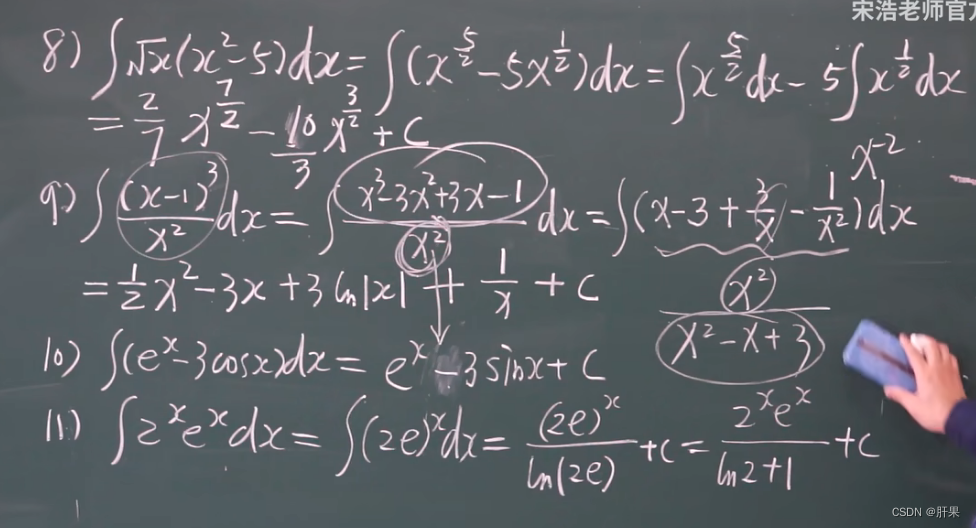
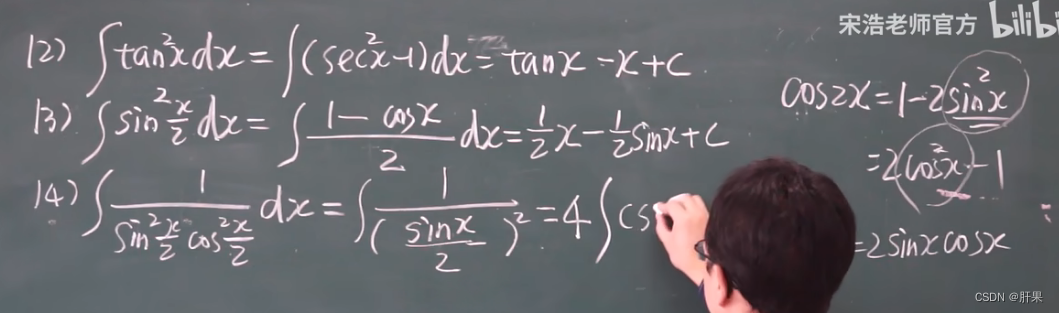
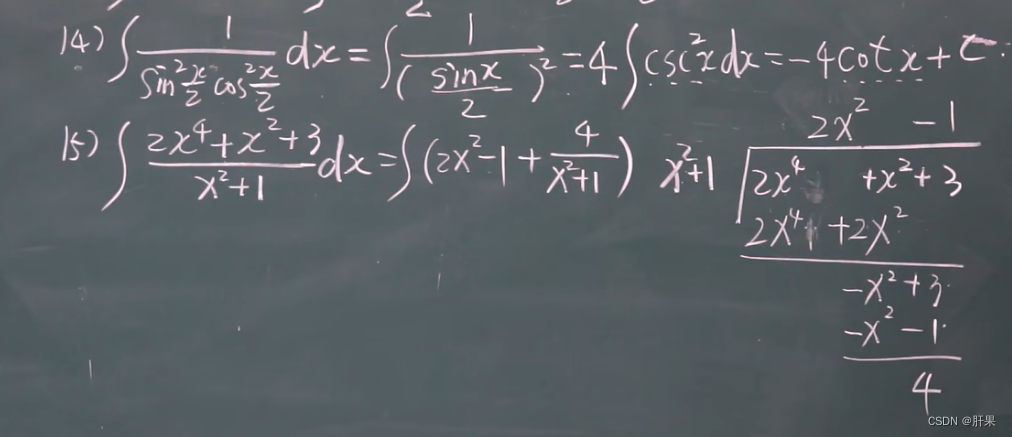
多项式除法:
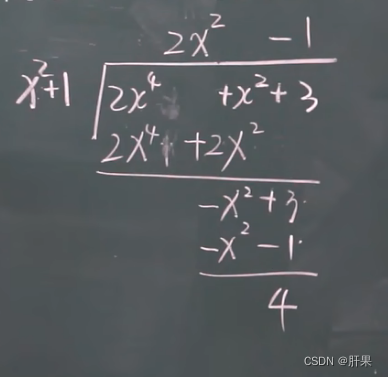
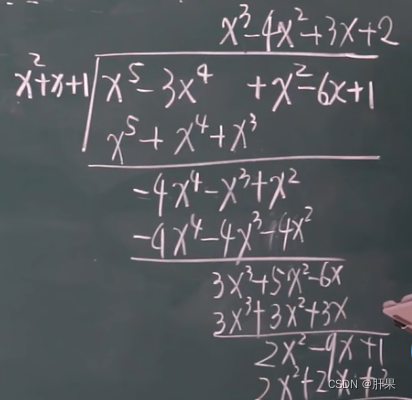
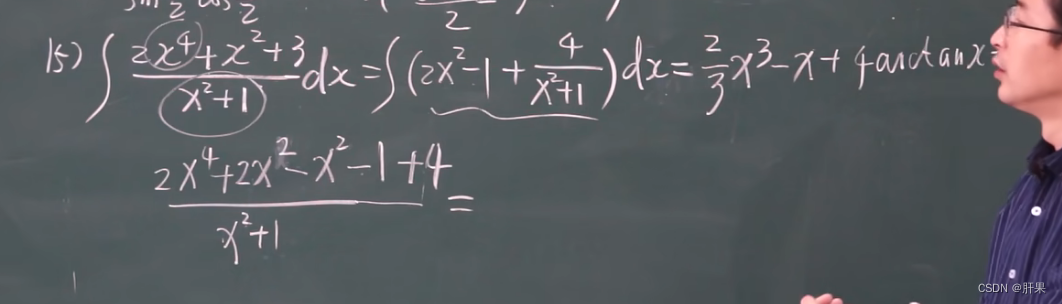
换元积分法(凑)

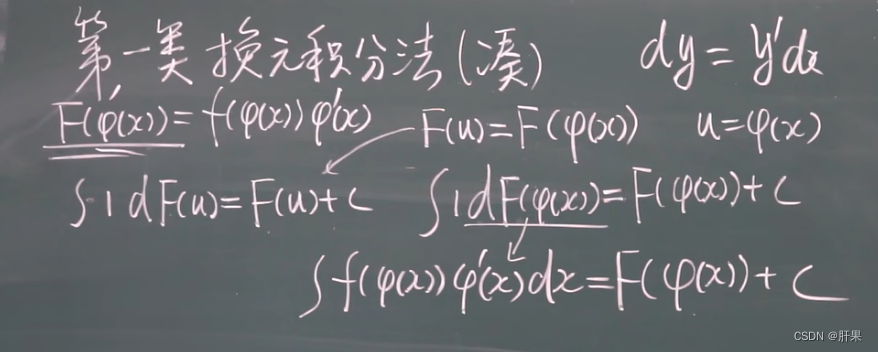
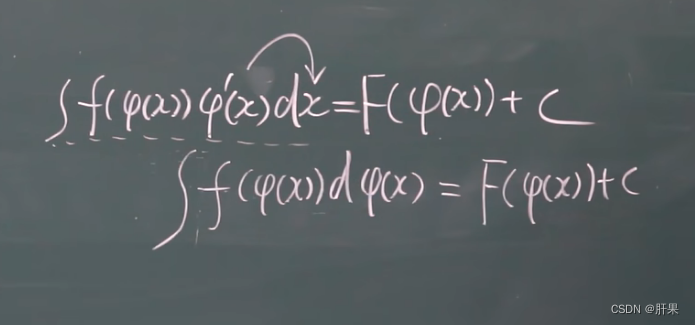

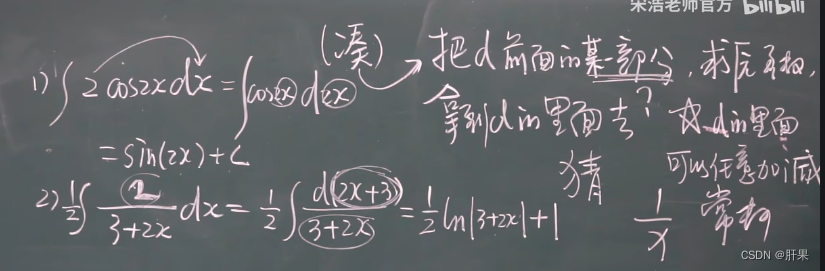
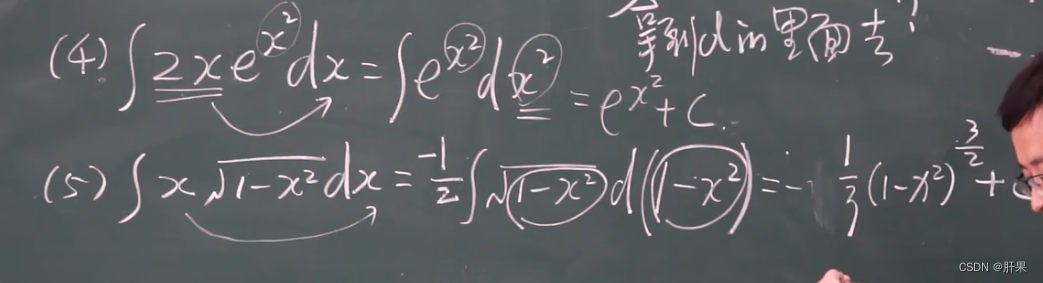
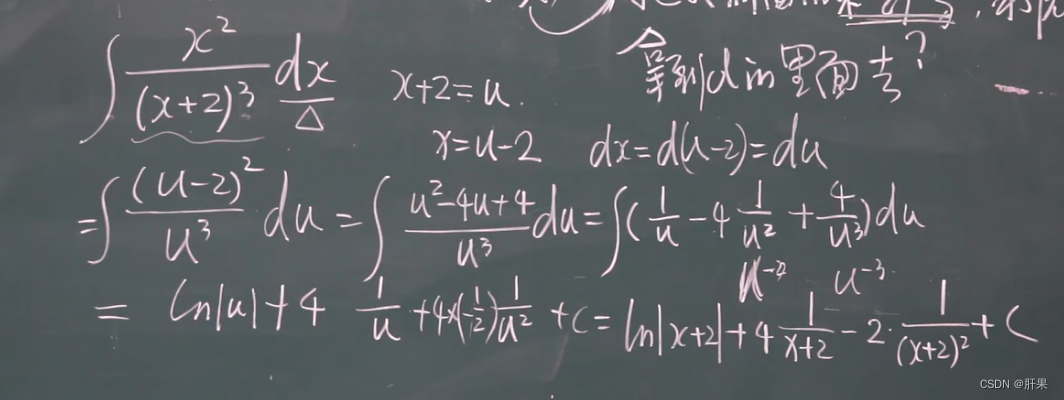
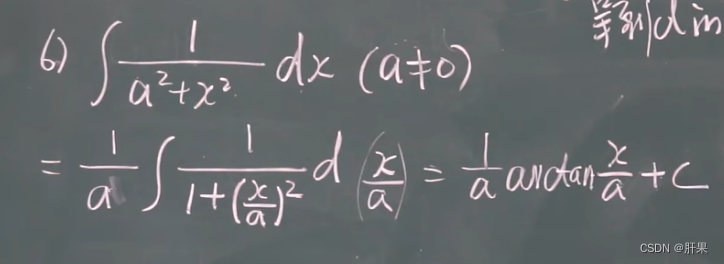


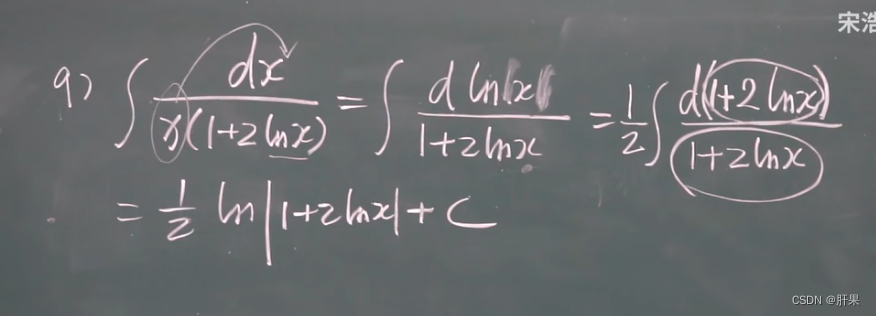
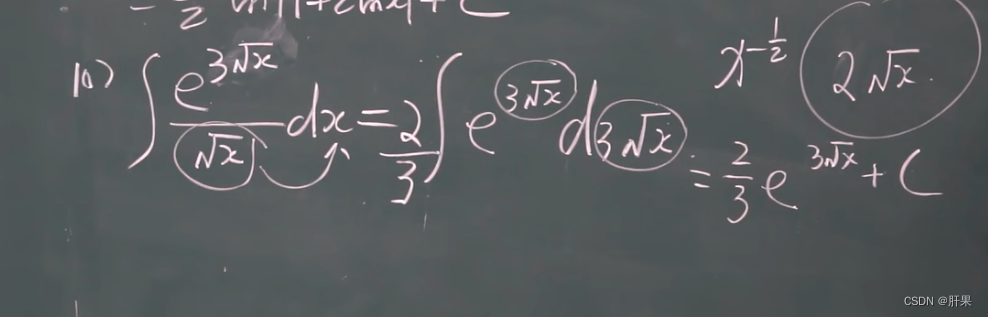
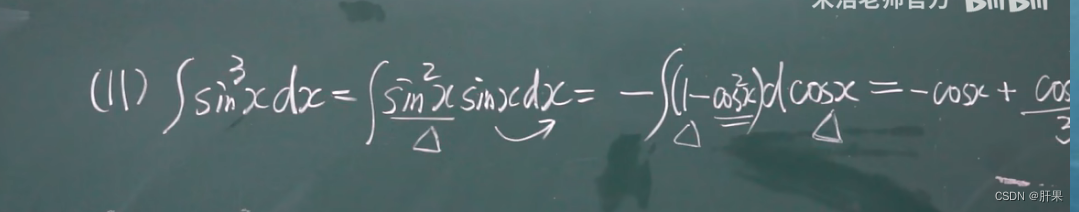
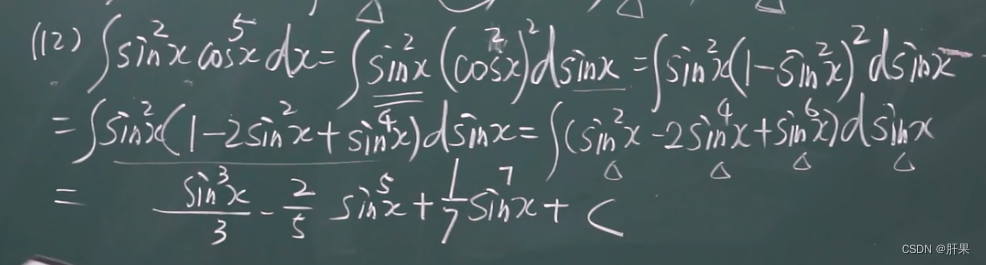
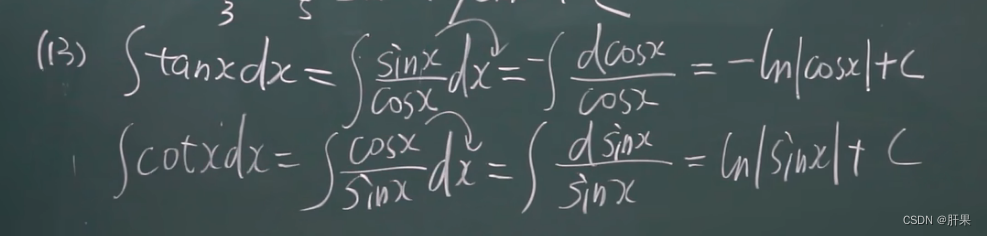
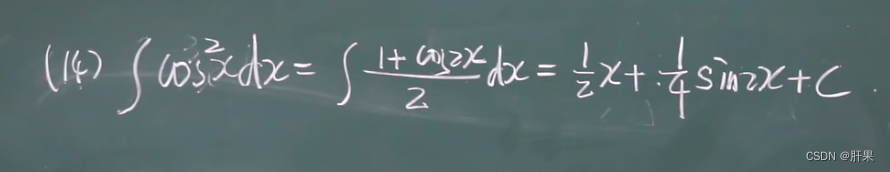
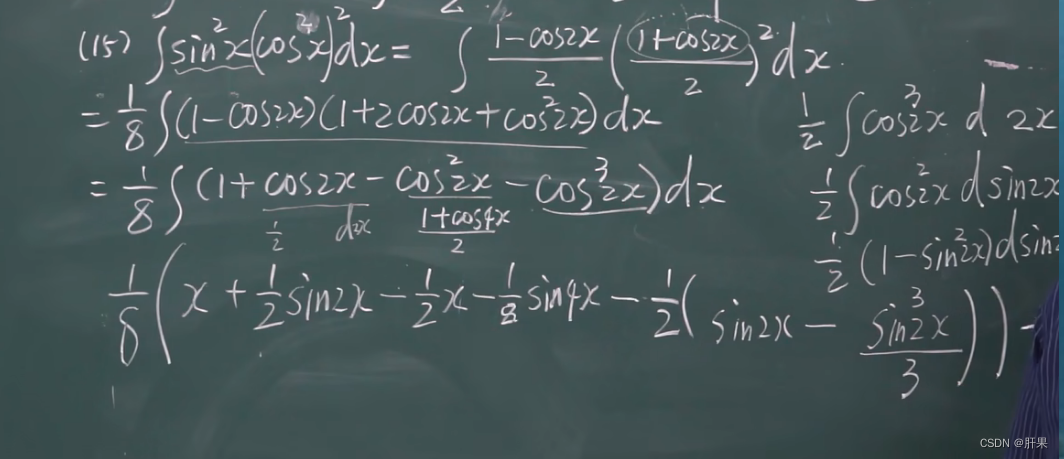
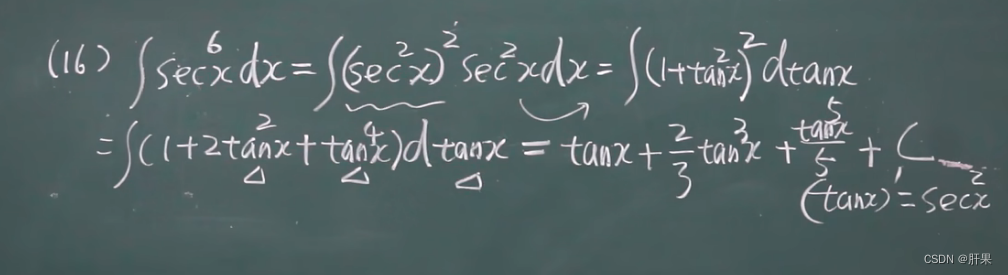
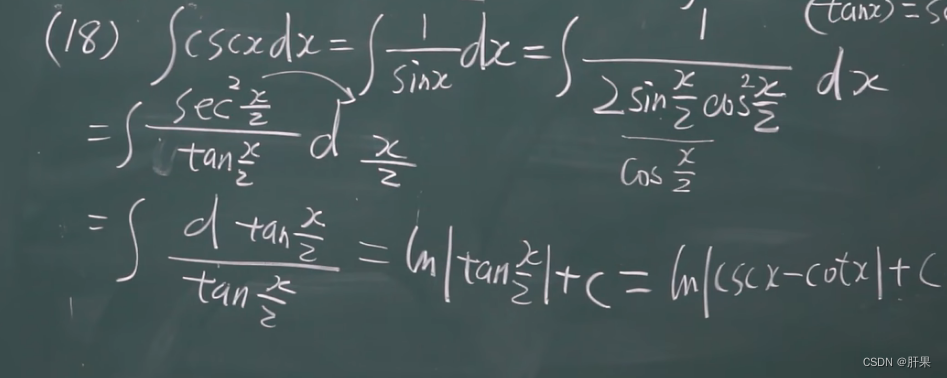
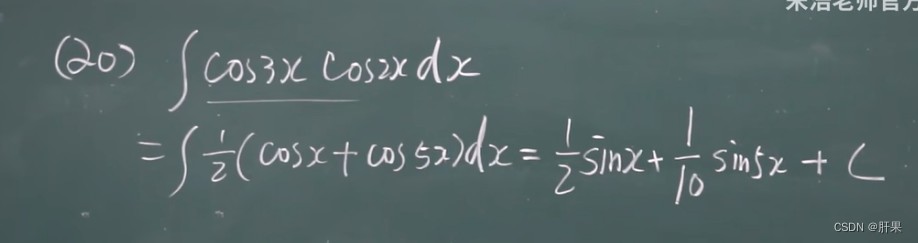
第二类换元积分法

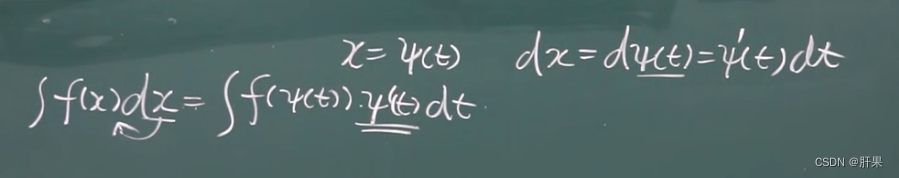
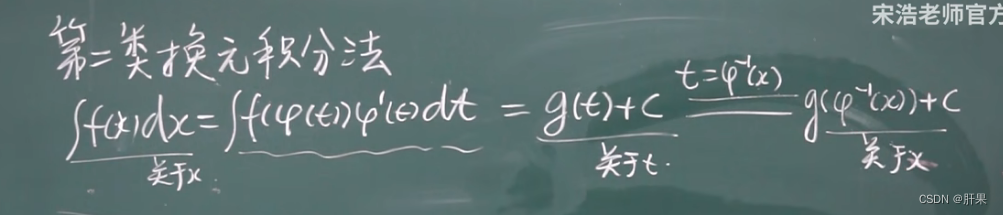

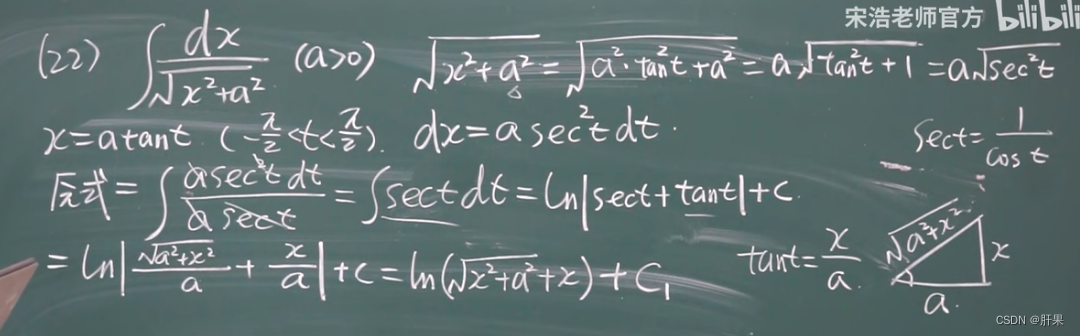
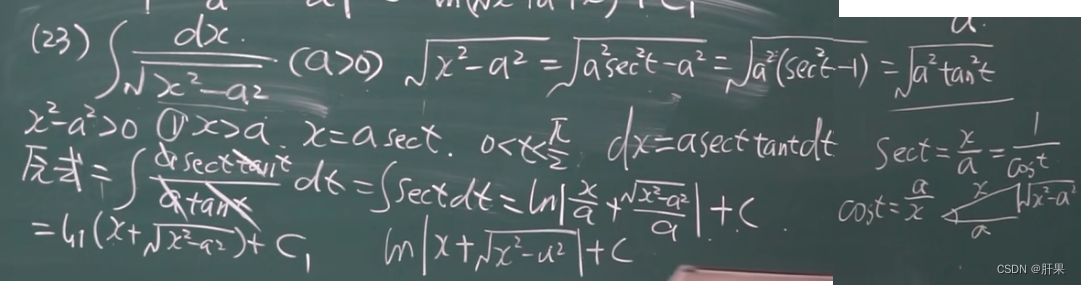


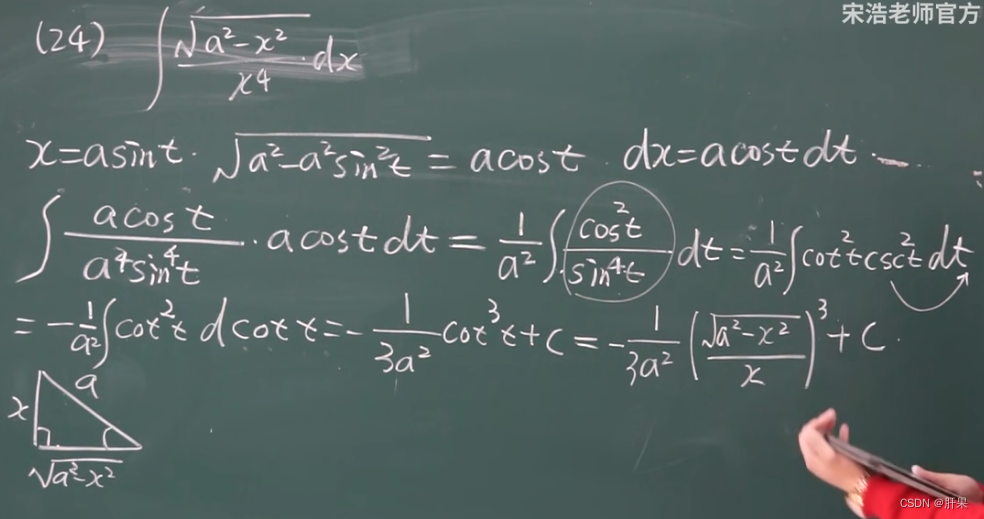
下表接前面内容。
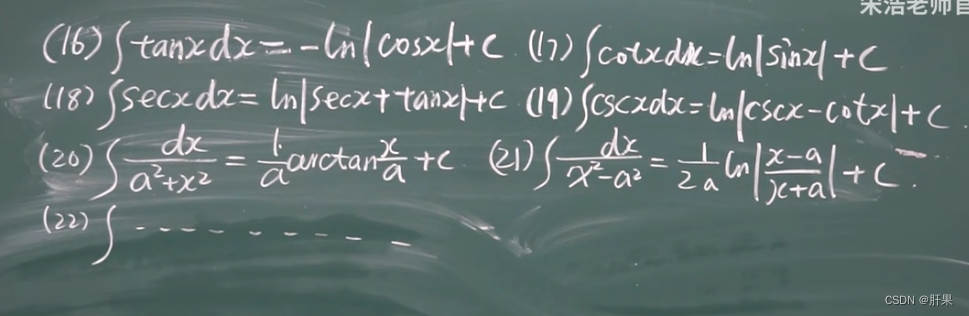
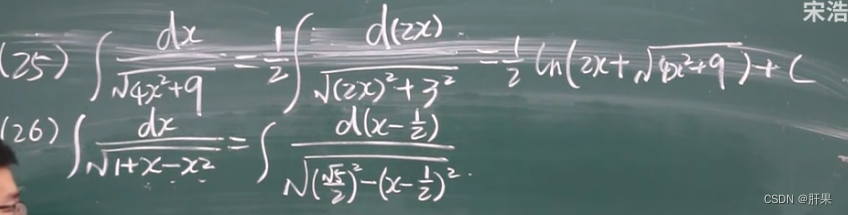
分部积分法(重要)

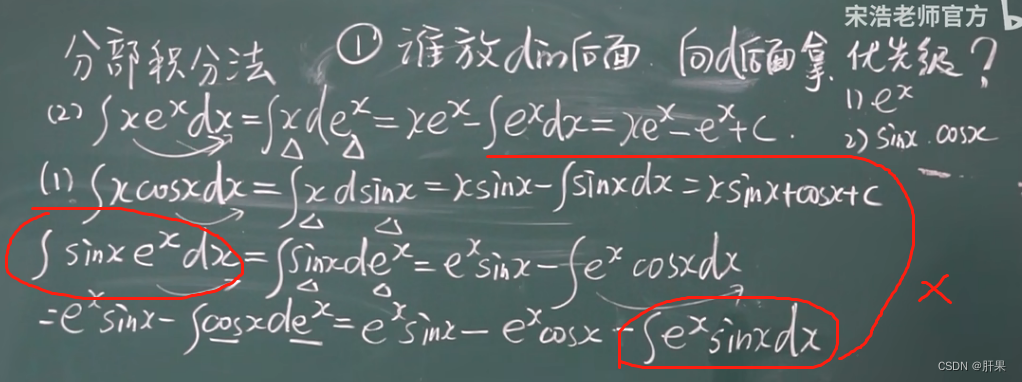





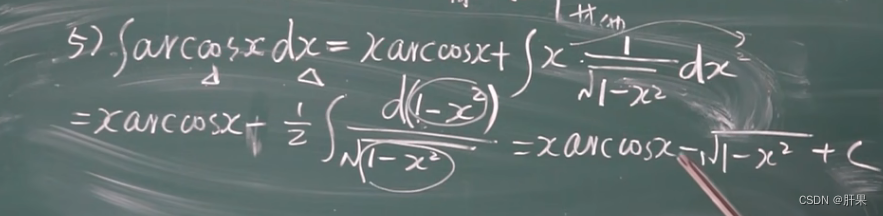
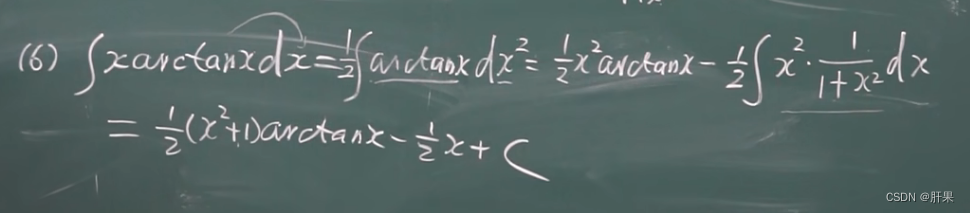
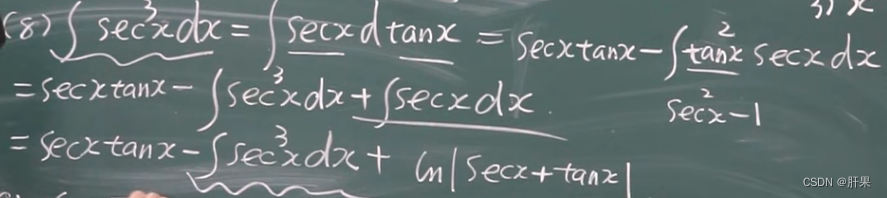
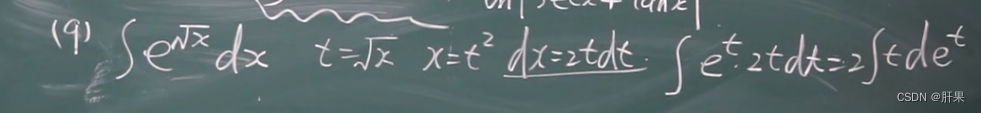
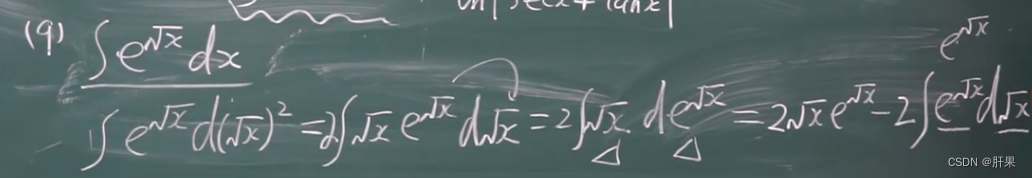
有理函数的积分
什么是有理函数?
有理函数(Rational function)是指形如P(x)/Q(x)的函数,其中P(x)和Q(x)都是多项式函数,而且Q(x)不为零。这里P(x)和Q(x)可以是实系数或复系数多项式。
有理函数在数学中具有重要的地位。它们在代数、分析、控制论等领域有广泛应用。有理函数的性质包括定义域、零点(使得分子为零)、极值点、不可约分等。
需要注意的是,在有理函数中,当Q(x)为零时会出现定义域的问题。此外,有理函数可能存在垂直渐近线和水平渐近线,这些也是它们特殊的性质