0 问题描述
假设有一个空间点集,不重合的点数有N个。
N=1时,最小包围盒是一个点:中心为其本身,半径无穷小
N=2时,最小包围盒是一个圆:中心为连线中点,半径为边长一半
N=3时,不共线的三点连成一个三角形,锐角和直角三角形其最小包围圆就是其外接圆。钝角三角形以最长边作为直径的圆是最小外接圆
N=4时,不共面的四点组成一个四面体,其最小包围球?如何计算?应该不一定是他的外接球。
那么
N>4,…
1 包围盒介绍
常见的包围盒种类有有以下4种:
①轴对齐包围盒AABB(Axis-aligned bounding box)
②包围球(Bounding Sphere)
③有向包围盒OBB(Oriented bounding box)
④固定方向凸包FDH(Fixed directions hulls或k-DOP)
1.1 AABB轴对齐包围盒
它被定义为包含该对象,且边平行于坐标轴的最小六面体。故描述一个AABB,仅需六个标量。AABB构造比较简单,存储空间小,但紧密性差,尤其对不规则几何形体,冗余空间很大,当对象旋转时,无法对其进行相应的旋转。处理对象是刚性并且是凸的,不适合包含软体变形的复杂的虚拟环境情况。
1.2 BS包围球
它被定义为包含该对象的最小的球体。确定包围球,首先需分别计算组成对象的基本几何元素集合中所有元素的顶点的x,y,z坐标的均值以确定包围球的球心,再由球心与三个最大值坐标所确定的点间的距离确定半径r。包围球的碰撞检测主要是比较两球间半径和与球心距离的大小。
1.3 OBB有向包围盒
OBB是较为常用的包围盒类型。它是包含该对象且相对于坐标轴方向任意的最小的长方体。OBB最大特点是它的方向的任意性,这使得它可以根据被包围对象的形状特点尽可能紧密的包围对象,但同时也使得它的相交测试变得复杂。OBB包围盒比AABB包围盒和包围球更加紧密地逼近物体,能比较显著地减少包围体的个数,从而避免了大量包围体之间的相交检测。但OBB之间的相交检测比AABB或包围球体之间的相交检测更费时。
1.4 FDH固定方向凸包
FDH(k-DOP)是一种特殊的凸包,继承了AABB简单性的特点,但其要具备良好的空间紧密度,必须使用足够多的固定方向。被定义为包含该对象且它的所有面的法向量都取自一个固定的方向(k个向量)集合的凸包。FDH比其他包围体更紧密地包围原物体,创建的层次树也就有更少的节点,求交检测时就会减少更多的冗余计算,但相互间的求交运算较为复杂。
2 包围盒计算算法
2.1 BS包围球计算算法
2.2.1 naive算法
一个最简单的思路就是,计算空间顶点在X、Y、Z方向上的最大值和最小值,那么就可以得到8个顶点组成的包围盒。取包围球中心为包围盒中心点,而包围球半径有的人认为可以取中心点到八个顶点的最大距离——这样其实并不严密。最好还是计算中心点到所有顶点距离的最大值:
2.2.2 ritter算法
另外一种算法是一个名为ritter提出来的,所以称为ritter算法。
首先计算出X方向上距离最远的两个点,Y方向上距离最远的两个点以及Z方向上距离最远的两个点。以这三个距离最远的范围作为初始直径,这三个距离的中心点作为初始球心。
然后依次遍历所有点,判断点是否在这个包围球内。如果不在,则更新包围球。如下图所示:
2.2.3 Welzl算法
很容易用递归算法来实现:
先根据 np-1 个点,生成一个球体(递归);
判断第 np 个点是否在球体内,是,则保持球体;
否,需要根据旧的球体和第 np 个点,生成新的球体(递归)。其中第 np 个点必在新生成的球面上;
递归结束条件:当一个点、两个点时,可直接生成球体;三个点都在球面上,则生成三角形的外接球;
3、现成代码库(包)
4、外接球与最小包围球的区别
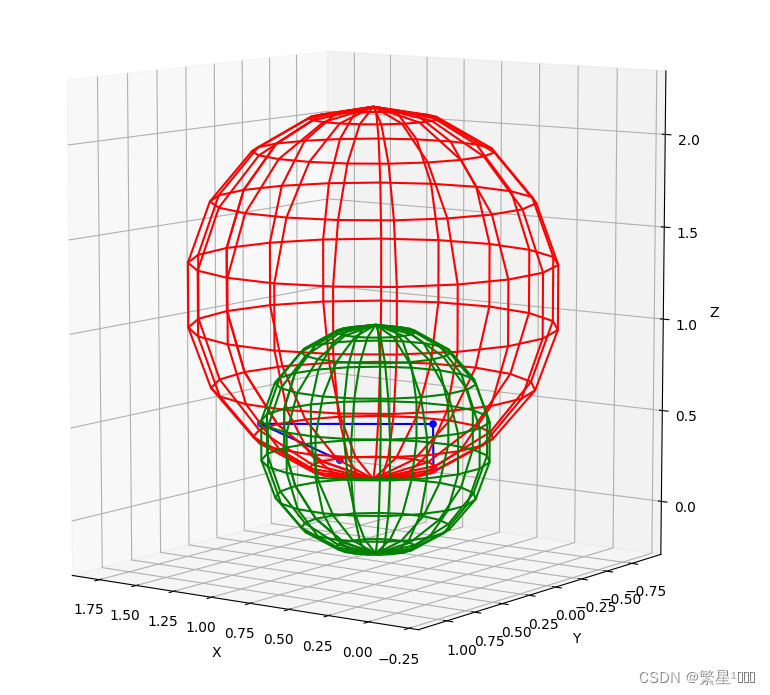
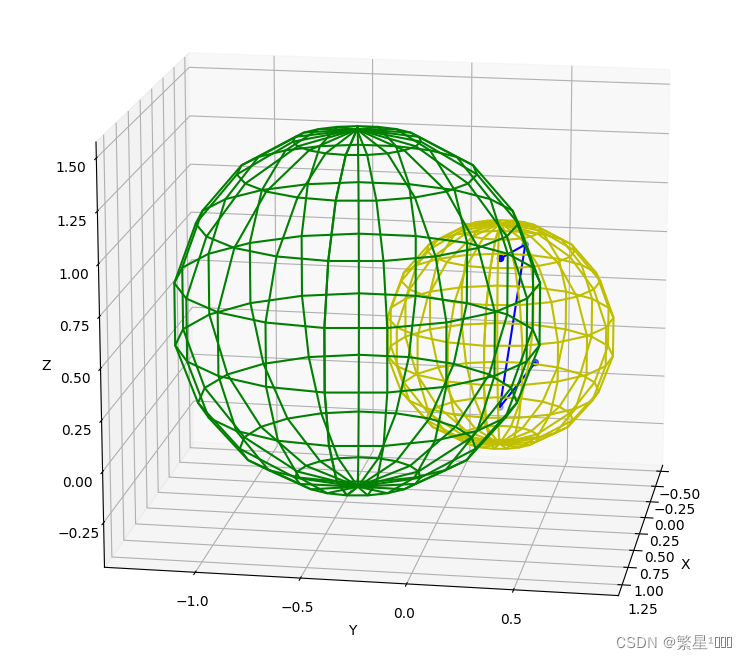
注意外接球和我理解的最小包围球是不一样的。
黄色的是最小包围球,绿色的是外接球

5、四点外接球与最小包围球的计算
import numpy as np
import matplotlib.pyplot as plt
def get_min_sphere_4points(points):
"""
Get the minimum radius of a circumscribed sphere that encloses all the points
"""
def minimum_enclosing_sphere_3points(triangle):
# Compute the circumcenter of the triangle
a, b, c = triangle
ab = b - a
ac = c - a
ab_cross_ac = np.cross(ab, ac)
ab_cross_ac_norm_sq = np.dot(ab_cross_ac, ab_cross_ac)
if ab_cross_ac_norm_sq == 0:
# Points are colinear, return a point and radius of infinity
return a, np.inf
ab_norm_sq = np.dot(ab, ab)
ac_norm_sq = np.dot(ac, ac)
circumcenter = a + (np.cross(ab_norm_sq * ac - ac_norm_sq * ab, ab_cross_ac) / (2 * ab_cross_ac_norm_sq))
# Calculate the radius of the circumcircle
radius = np.linalg.norm(circumcenter - a)
# Check if the circumcenter lies inside the triangle
if np.all(np.logical_and(circumcenter >= a, circumcenter <= c)):
return circumcenter, radius
# Otherwise, the minimum enclosing sphere is the circumcircle
else:
center = np.mean(triangle, axis=0)
radius = np.max(np.linalg.norm(triangle - center, axis=1))
return center, radius
def _min_sphere(points, center, radius):
if len(points) == 0 or len(center) == 3:
if len(center) == 3:
# c1, c2, c3 = center
# return np.array([(c1 + c2 + c3) / 3]), 0
return minimum_enclosing_sphere_3points(center)
elif len(center) == 2:
c1, c2 = center
return (c1 + c2) / 2, np.linalg.norm(c1 - c2) / 2
elif len(center) == 1:
return center[0], 0
else:
return None, 0
else:
p = points[0]
points = points[1:]
c, r = _min_sphere(points, center, radius)
if c is None or np.linalg.norm(p - c) > r:
center.append(p)
c, r = _min_sphere(points, center, radius)
center.pop()
return c, r
if len(points) < 4:
raise ValueError("At least 4 points are required.")
np.random.shuffle(points)
center, radius = _min_sphere(points, [], 0)
print("Center:", center)
print("Radius:", radius)
return center, radius
def fit_circumscribed_sphere_4points(array, tol=1e-6):
# Check if the the points are co-linear
D12 = array[1] - array[0]
D12 = D12 / np.linalg.norm(D12)
D13 = array[2] - array[0]
D13 = D13 / np.linalg.norm(D13)
D14 = array[3] - array[0]
D14 = D14 / np.linalg.norm(D14)
chk1 = np.clip(np.abs(np.dot(D12, D13)), 0., 1.) # 如果共线,chk1=1
chk2 = np.clip(np.abs(np.dot(D12, D14)), 0., 1.)
# 求的是反余弦值,如果是1,反余弦值为0(弧度),乘以180/pi,就是0(度),说明共线
if np.arccos(chk1) / np.pi * 180 < tol or np.arccos(chk2) / np.pi * 180 < tol:
R = np.inf
C = np.full(3, np.nan)
return R, C
# Check if the the points are co-planar
n1 = np.linalg.norm(np.cross(D12, D13))
n2 = np.linalg.norm(np.cross(D12, D14))
chk = np.clip(np.abs(np.dot(n1, n2)), 0., 1.)
if np.arccos(chk) / np.pi * 180 < tol:
R = np.inf
C = np.full(3, np.nan)
return R, C
# Centroid of the sphere
A = 2 * (array[1:] - np.full(len(array) - 1, array[0]))
b = np.sum((np.square(array[1:]) - np.square(np.full(len(array) - 1, array[0]))), axis=1)
C = np.transpose(np.linalg.solve(A, b))
# Radius of the sphere
R = np.sqrt(np.sum(np.square(array[0] - C), axis=0))
print("Center:", C)
print("Radius:", R)
return C, R
if __name__ == '__main__':
# # Define the four points
p1 = np.array([0, 0, 0])
p2 = np.array([0, 4, 0])
p3 = np.array([4, 0, 0])
p4 = np.array([1, 2, 0])
points1 = np.array([p1, p2, p3, p4])
points1 = np.random.rand(4, 3)
# show_tetrahedron(points1)
center0, radius0 = fit_circumscribed_sphere_4points(points1)
center1, radius1 = get_min_sphere_4points(points1)
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Plot the points
ax.scatter(points1[:, 0], points1[:, 1], points1[:, 2], c='b')
# plot the tetrahedron
ax.plot(points1[:, 0], points1[:, 1], points1[:, 2], c='b')
# Plot the sphere1
u, v = np.mgrid[0:2 * np.pi:20j, 0:np.pi:10j]
x = center0[0] + radius0 * np.cos(u) * np.sin(v)
y = center0[1] + radius0 * np.sin(u) * np.sin(v)
z = center0[2] + radius0 * np.cos(v)
ax.plot_wireframe(x, y, z, color="g")
# Plot the sphere2
u, v = np.mgrid[0:2 * np.pi:20j, 0:np.pi:10j]
x = center1[0] + radius1 * np.cos(u) * np.sin(v)
y = center1[1] + radius1 * np.sin(u) * np.sin(v)
z = center1[2] + radius1 * np.cos(v)
ax.plot_wireframe(x, y, z, color="y")
# Set the axes properties
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_aspect('equal')
# Show the plot
print('Showing the plot...')
plt.show()
参考文献
最小包围球:naive算法和ritter算法
最小包围球:welzl算法