来自Manolis Kellis教授（MIT计算生物学主任）的课《人工智能与机器学习》

主要内容是表示学习（Representation Learning）的part2----

压缩（自动编码器）、捕捉参数分布（VAE）、使用第二个网络（GAE）三种方式来进行Representation Learning

上一节知识回顾：介绍了表示学习定义和第一种方式：Pretext Text

本节内容跟以前的一篇博客高度重合，学习模型原理参考：生成模型（自编码器、VAE、GAN）。这里更偏重从数据中使用方法来学习到有意义的表示z。

下面贴出油管链接：

Generative Models, Adversarial Networks GANs, Variational Autoencoders VAEs, Representation Learning

Compression:Auto-Encoders

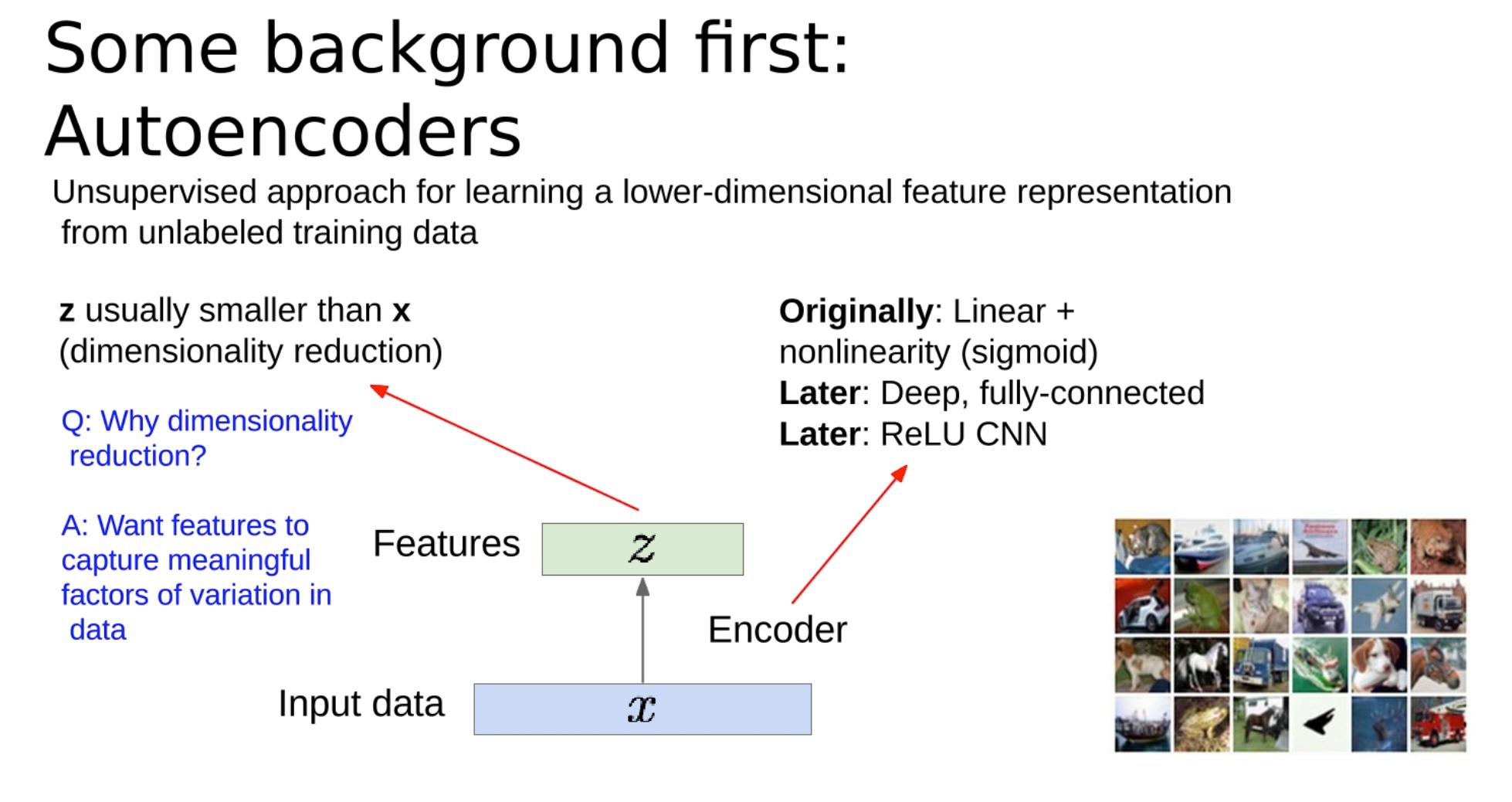
自动编码器是一种用于学习输入数据有效编码的人工神经网络。这是一种无监督学习方法，意味着它不需要标记的训练数据。

• 自动编码器的结构包括一个编码器和一个解码器：

  1. 编码器 减少输入数据（记为X）的维度，创建一个压缩表示，通常称为潜在空间表示或编码（记为Z）。目标是以这样的方式降低维度，使得特征可以捕捉数据中有意义的变化因素。这个Z就是我们要学习的有意义的东西

  2. 解码器 获取压缩数据并重构原始输入数据。这里的想法是，一个好的编码是可以用来准确重建原始数据的。

• 降维的原因：

  1. 它减少了模型的计算复杂性和存储需求。

  2. 更重要的是，它迫使自动编码器学习一个紧凑的表示，捕捉数据中的基础结构或模式，基本上是数据的’本质’。

  3. 通过压缩（z的维度小）来实现表征学习。

  4. 输入和输出其实都是x，所以不需要额外的标签y

最初，自动编码器是作为使用线性激活函数的全连接神经网络来实现的，后来使用了如Sigmoid这样的非线性激活函数。随着时间的推移，引入了深度和更复杂的结构，如使用ReLU（Rectified Linear Unit）非线性激活函数的卷积神经网络（CNN）。

自动编码器可用于各种任务，如异常检测，去噪，以及用于数据可视化的降维。

在训练自动编码器时，我们希望特征可以用来重建原始数据。这不需要标签，因此这是一种无监督学习。训练通常通过最小化L2损失函数（也称为均方误差）来完成，该函数测量原始输入和重建输入之间的差距。

图中右侧的例子中，编码器和解码器分别由四层卷积（conv）和四层反卷积（upconv）构成。

训练之后，我们可以丢弃解码器部分，只保留编码器部分。编码器现在可以作为一种特征提取器，将输入数据转化为压缩的特征表示。

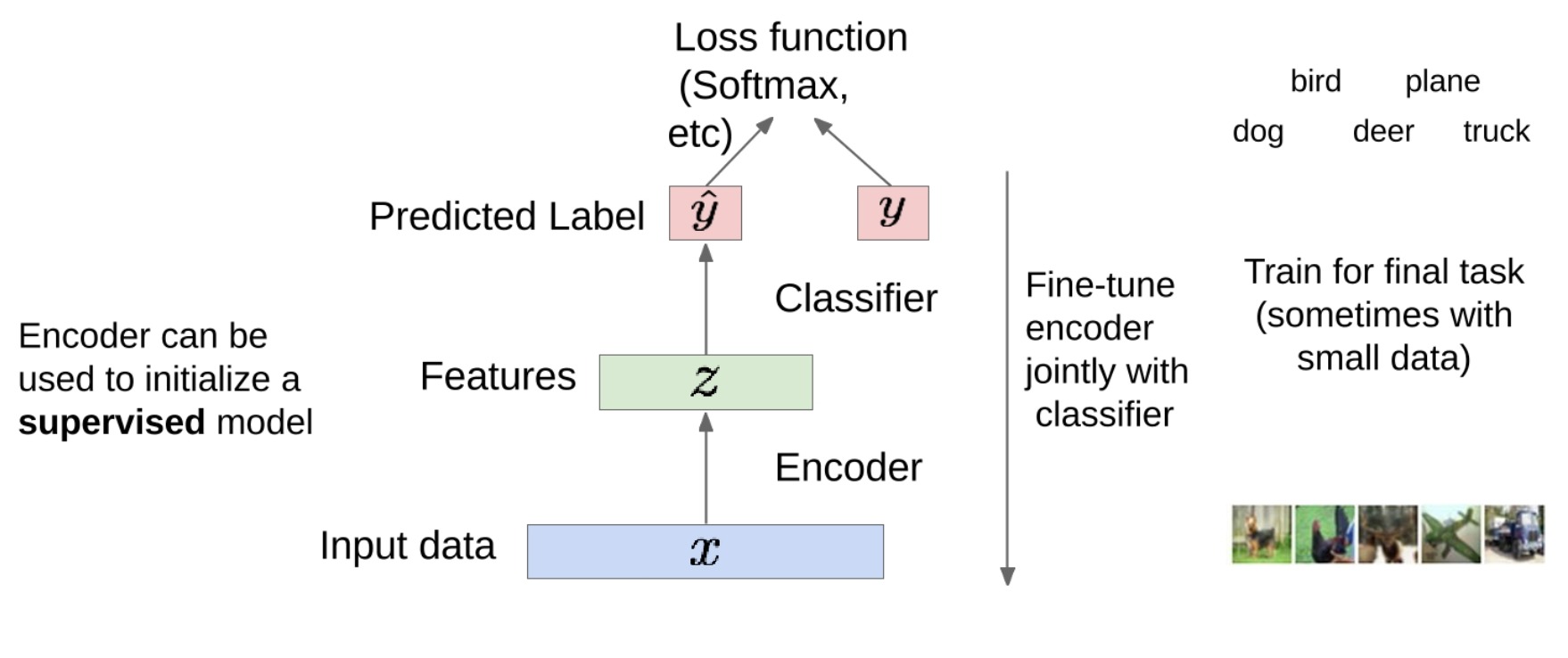
然后，我们可以将这些特征用于最终任务的训练，例如分类。在这种情况下，我们需要标签，因此这是一种监督学习。

具体来说，我们可以在编码器的输出端连接一个分类器。分类器可以使用softmax、交叉熵等损失函数来训练，以预测每个类别的概率。

然后，我们可以对整个模型进行微调。这意味着我们不仅更新分类器的权重，也同时更新编码器的权重。这样可以使编码器更好地适应最终的任务。

在小数据情况下，这种方法尤其有用，因为编码器已经在大量无标签数据上进行了预训练，因此它已经学会了捕捉数据中的一些基本模式。这使得它能够在少量标签数据上快速并有效地进行微调。如果不先在大量数据上训练的话，在小数据集是难以实现预测的。

自动编码器可以重构数据，并可以学习特征以初始化监督模型。它们能够捕捉训练数据中的变化因素，那么我们是否可以从自动编码器中生成新的图像呢？

这个问题引出了变分自动编码器（Variational Autoencoders，简称VAE）。

变分自动编码器是一种特殊类型的自动编码器，它不仅可以重构数据，还可以生成新的、从未见过的数据。这使得VAE在生成模型领域（例如，生成新的图像或文本）中非常有用。

Capture parameter distribution (variance): Variational Auto-Encoders

原理介绍

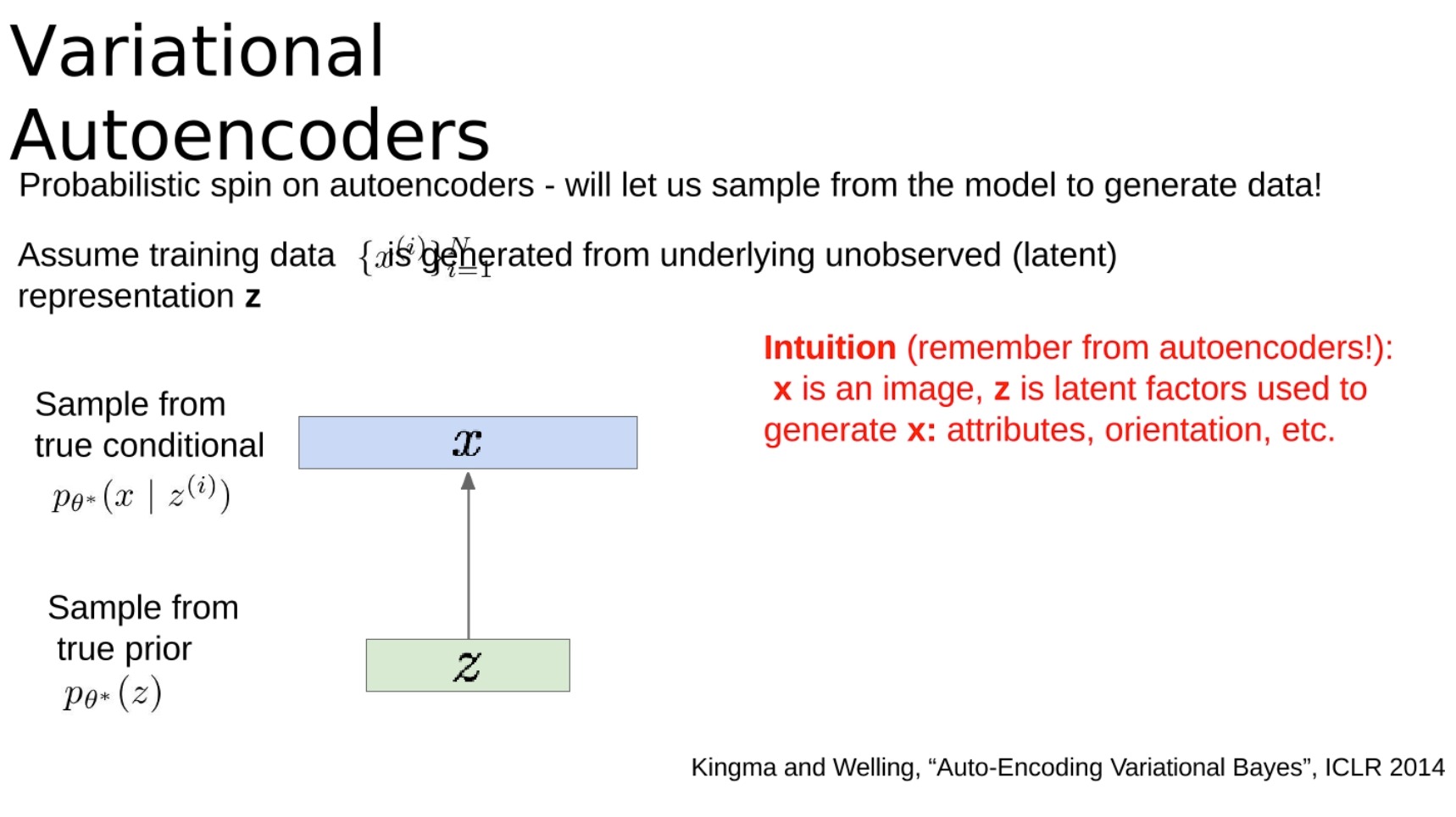
变分自动编码器对自动编码器进行了概率性的解释，这使我们能从模型中抽样以生成数据！假设训练数据 $X$ 是由未观察（潜在）表示$Z$生成的。

直观来看（回想一下自动编码器的内容！）：$X$是一张图像，$Z$是用于生成$X$的潜在因素：属性，方向等。

• 我们希望估计这个生成模型的真实参数$ θ*$ 。

  • 如何表示这个模型呢？

    • 选择先验$p(Z)$为简单的形式，例如高斯分布。
    • 条件$p(x|z)$（生成图像） => 用神经网络表示，因为她太过复杂。
    • 

  • 如何训练模型呢？

    • 回忆一下从贝叶斯网络中学习生成模型的策略。学习模型参数，以最大化训练数据的似然(我们需要找到一组模型参数，使得训练数据在模型下的似然性（likelihood）最大)：

    • $p_{\theta }(x)=\int p_{\theta }(x)p_{\theta }(x|z)dz$

    • 现在引入潜在变量z,情况变复杂了，下面有解释。

    • 

• 以上内容引用自Kingma和Welling的论文"Auto-Encoding Variational Bayes"，ICLR 2014。

用gpt4简单的举一个例子：

假设你是一个艺术品商人，你的任务是创建一种机器，它可以生成尽可能真实的梵高的画作复制品。首先，你需要收集梵高的一些原作来训练你的机器。这就是你的训练数据。

现在，你有了一个基本的自动编码器。你让它看梵高的画，然后让它试着重现这些画。自动编码器的编码部分试图了解梵高的画作的一些基本特征（例如色彩、画风、主题等），并将这些特征抽象为一种称为潜在表示的形式。解码部分则试图从这些潜在表示中重建梵高的原始画作。通过反复试错，自动编码器学会了如何较好地复制梵高的画作。

但是现在有一个问题：如果你想让机器创作出全新的、看起来像梵高画作的画，你该怎么做呢？这就是变分自动编码器（VAE）派上用场的地方。

在变分自动编码器中，我们不仅要求机器学会如何复制梵高的画作，还要求它理解梵高画作背后的一些基本规则。我们希望机器能够创建一种“梵高画作的可能空间”，在这个空间中，每一点都对应一种可能的梵高风格的画作。

具体来说，我们希望编码器不仅仅给出一个固定的潜在表示，而是给出一个潜在表示的概率分布。这样，我们可以从这个分布中随机抽样，得到一些新的潜在表示，然后通过解码器将这些潜在表示转化为新的画作。

在我们的例子中，这就好像机器不仅仅学会了如何复制梵高的画作，还理解了梵高的画作背后的一些基本规则，如何搭配色彩，如何选择主题等。因此，即使给定一个从未见过的潜在表示，机器也能够根据这些规则创作出一幅新的、看起来像梵高的画。

• 解释$p_{\theta }(x)=\int p_{\theta }(x)p_{\theta }(x|z)dz$：

“似然性”是一个概率术语，它表示给定模型和模型参数时，观察到实际数据的可能性有多大。通过最大化似然性，我们就是在找到一组参数，使得模型生成训练数据的可能性最大。

这个策略在训练FVBN时是有效的，但当我们引入潜在变量z时，情况就变得复杂了。潜在变量z是我们在模型中引入的一种隐藏变量，它代表了一些我们不能直接观察到的因素，例如在我们的梵高画作的例子中，z可能表示梵高的画风、色彩搭配等。

在有了潜在变量z之后，我们不能直接计算训练数据的似然性，因为我们不知道z的真实值。为了解决这个问题，我们使用了上面公式中的积分来对所有可能的z值进行求和。这个积分表示，我们考虑了所有可能的z值，然后计算了在这些z值下，训练数据的似然性的总和。

但是，直接计算这个积分通常是非常困难的，特别是当z的维度很高时。这就是为什么我们需要使用一些近似方法，例如变分推断（内容如下），来近似这个积分。变分自动编码器就是使用这种策略的一个例子。

• 问：这样做的问题是什么？ 答：难以处理！

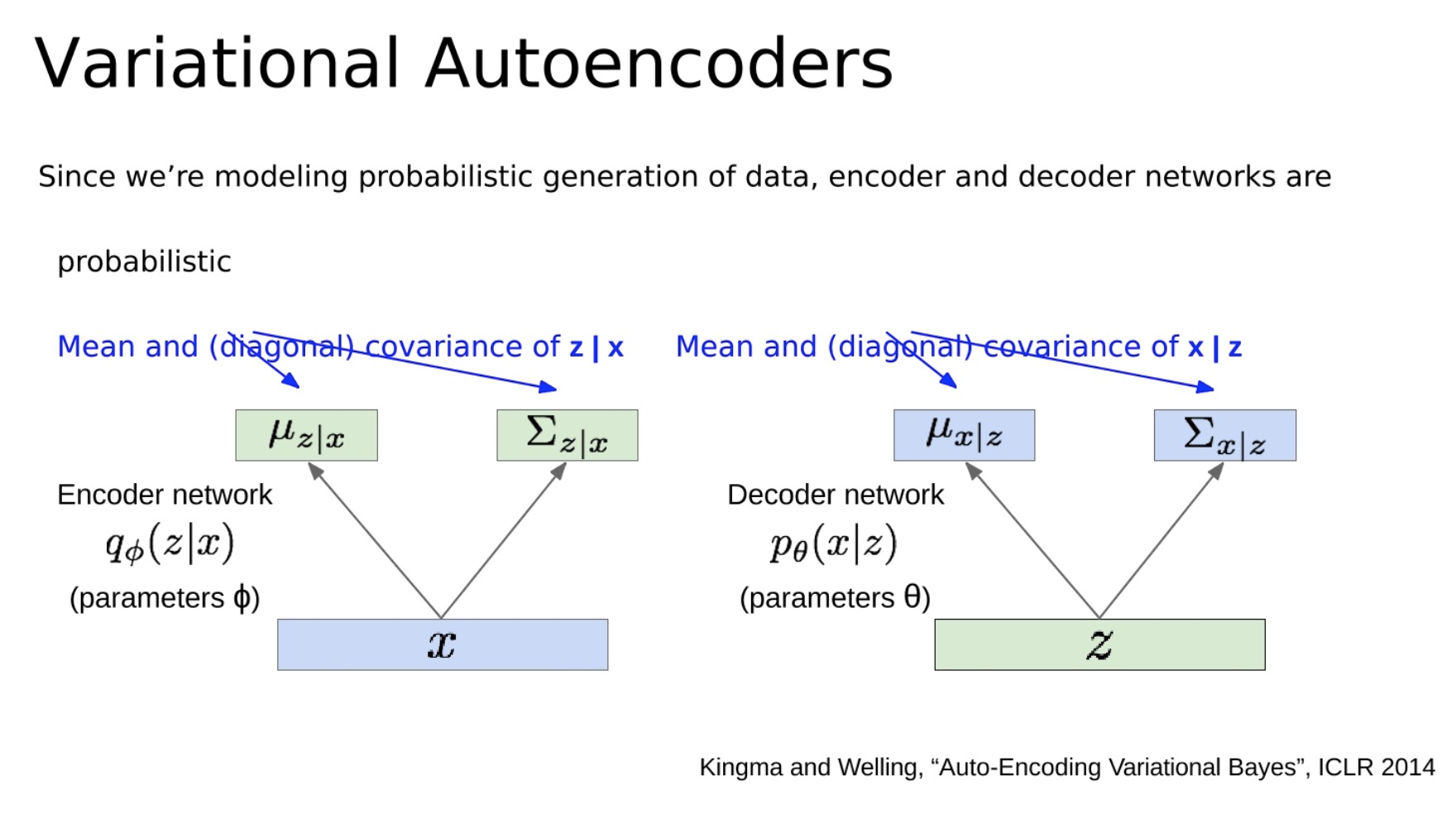
• 由于我们正在对数据的概率生成进行建模，所以编码器和解码器网络是概率性的。它们对潜在变量z的条件均值和（对角）协方差进行建模，以及对x的条件均值和（对角）协方差进行建模。

在传统的自动编码器中，编码器输出的是一个确定的潜在向量z，这个向量直接被用来通过解码器重构输入数据x。然而，在VAE中，编码器实际上输出的是一个潜在向量z的概率分布的参数（通常是一个高斯分布的均值和协方差）。这意味着，潜在向量z现在是不确定的，**它可以是从这个概率分布中采样得到的任何值。**这就引入了一个额外的随机性，使得VAE能够生成新的、不同的数据。

同时，解码器不再直接生成重构的数据x，而是**生成一个关于x的概率分布的参数（**通常也是一个高斯分布的均值和协方差）。这意味着，给定一个潜在向量z，我们可以生成出各种不同的数据x，它们都符合解码器给出的概率分布。

这种概率性的建模方式使得VAE能够更好地模拟数据的生成过程，并允许我们从模型中采样生成新的、不同的数据。这是VAE作为一种生成模型的关键特性。

• 问题在于，这种模型的训练涉及到对一些概率分布的积分进行计算，而这通常是**难以处理（Intractable）**的。例如，我们需要计算所有可能的潜在变量z对应的概率的积分，但这在计算上是不可行的，尤其是当潜在空间的维度较高时。

  • 在VAE中，编码器网络（也被称为推断网络）试图学习潜在变量z的后验概率分布P(z|x)的参数。然后，解码器网络（也被称为生成网络）试图学习观察变量x的概率分布P(x|z)的参数。

  • VAE的关键思想是引入了一种变分推断的方法，用来近似这些难以处理的概率分布。具体来说，我们引入了一个易于处理的近似分布Q(z|x)，并试图使这个分布尽可能接近真实的后验分布P(z|x)。然后，我们可以通过最大化这个近似分布的变分下界（也被称为ELBO，Evidence Lower BOund），来训练模型的参数。

• 这就是为什么虽然VAE的训练涉及到一些难以处理的概率分布，但我们仍然可以有效地训练它的原因。

• 插入一篇我以前写的博客：生成模型（自编码器、VAE、GAN）

数学推导

变分自动编码器（Variational Autoencoders，VAE）的数学推导，其中包括对数似然性和KL散度的计算。

在VAE中，我们的目标是最大化数据的对数似然性，即$logP(x)$，其中x是我们的训练数据。由于我们的模型包含潜在变量z，所以这个似然性需要对所有可能的z值求和，这通常是不可计算的。因此，我们需要找到一种方法来近似这个似然性。

我们的策略是引入一个近似后验分布$q(z|x)$，来近似真实的后验分布$p(z|x)$。在VAE中，我们通常选择$q(z|x)$为一个高斯分布，其均值和协方差是由编码器网络给出的。

然后，我们可以将对数似然性$logP(x)$重写为两个部分的和：

1. 第一部分是期望的对数似然性$E[logP(x|z)]$，其中z是从$q(z|x)$中采样得到的
2. 第二部分是$q(z|x)$和$p(z|x)$之间的KL散度$D_{KL}(q(z|x)||p(z|x))$。

然后，我们可以进一步将KL散度重写为$q(z|x)$和先验分布$p(z)$之间的KL散度，以及一个额外的修正项。

在上面的推导中，我们可以看到：

1. 第一部分（期望的对数似然性）可以通过重参数化技巧来进行采样估计。这意味着，我们可以用一个小批量的样本z，从$q(z|x)$中采样，然后计算$x|z$的似然性。由于重参数化技巧，这个过程是可以微分的，所以我们可以用梯度下降法来优化。

2. 第二部分（KL散度）可以通过解析解来计算，因为我们知道$q(z|x)$和$p(z)$都是高斯分布，它们之间的KL散度有闭形式解。

因此，我们可以通过优化这两部分的和来训练我们的VAE模型。

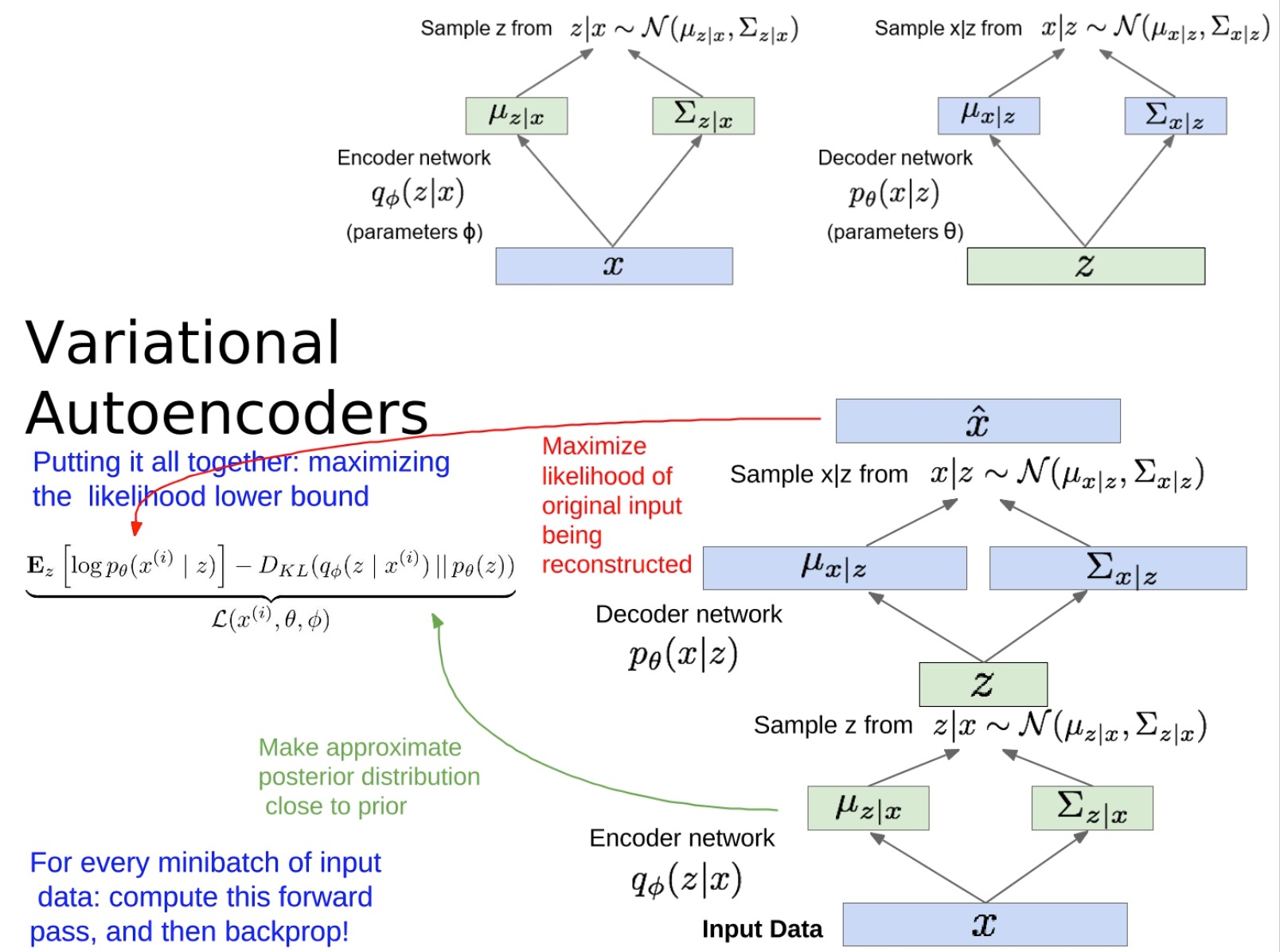
• 这段内容总结了如何训练一个VAE。

  • 先让输入数据通过编码器网络，得到潜在变量z的分布参数，然后从这个分布中抽样得到z。接着，让z通过解码器网络，得到重构输入的分布参数，并从这个分布中抽样得到重构的输入。目标是让这个重构的输入尽可能接近原始的输入，这就是**“重构输入”**的部分。
  • 另外，我们还希望让编码器给出的潜在变量z的分布接近我们选择的先验分布，通常是一个标准正态分布。这就是“让近似后验分布接近先验分布”的部分。我们通过计算编码器给出的分布和先验分布之间的KL散度来实现这个目标。

• 训练模型的时候，就是通过优化上述两部分的和来进行的。这个和就是所谓的“证据下界（Evidence Lower BOund，ELBO）”，我们的目标是让这个下界尽可能大。为了优化这个下界，我们可以使用随机梯度下降法，对每个小批量的输入数据，先计算一次前向传播，得到ELBO的值，然后再进行反向传播，更新模型的参数。

在实际操作中，由于计算期望值需要进行积分，而直接积分通常是非常困难的，所以我们通常使用蒙特卡罗方法来近似这个积分。也就是说，我们从编码器给出的分布中抽样多次，然后计算样本的平均值，作为期望值的估计。

生成数据

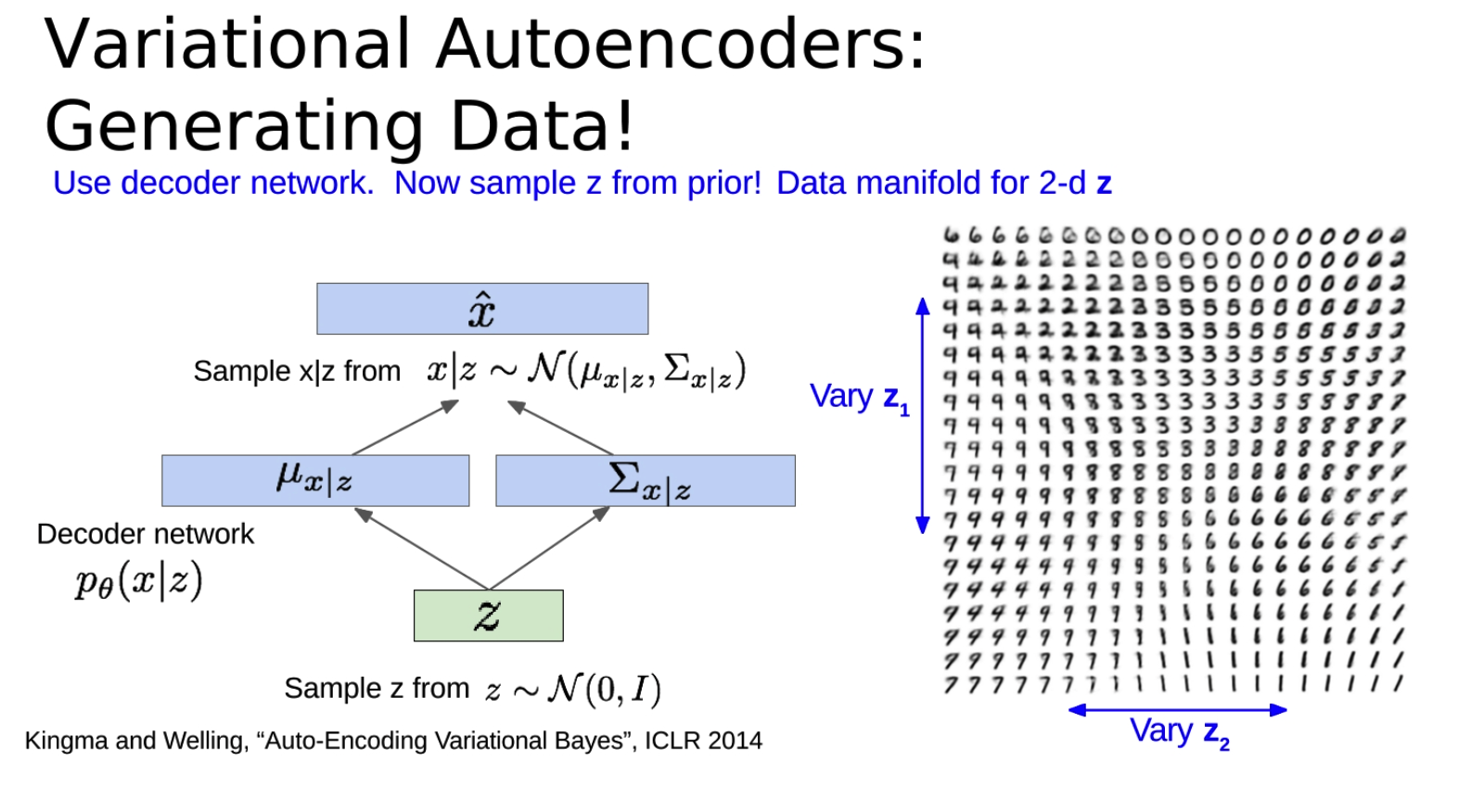
• 关于如何使用训练好的变分自动编码器（VAE）进行数据生成。

  • 首先，从先验分布（通常是标准正态分布）中采样得到潜在变量z，然后将z输入到解码器网络中，得到重构输入的分布参数，并从这个分布中抽样得到生成的数据。这就是VAE的生成过程。

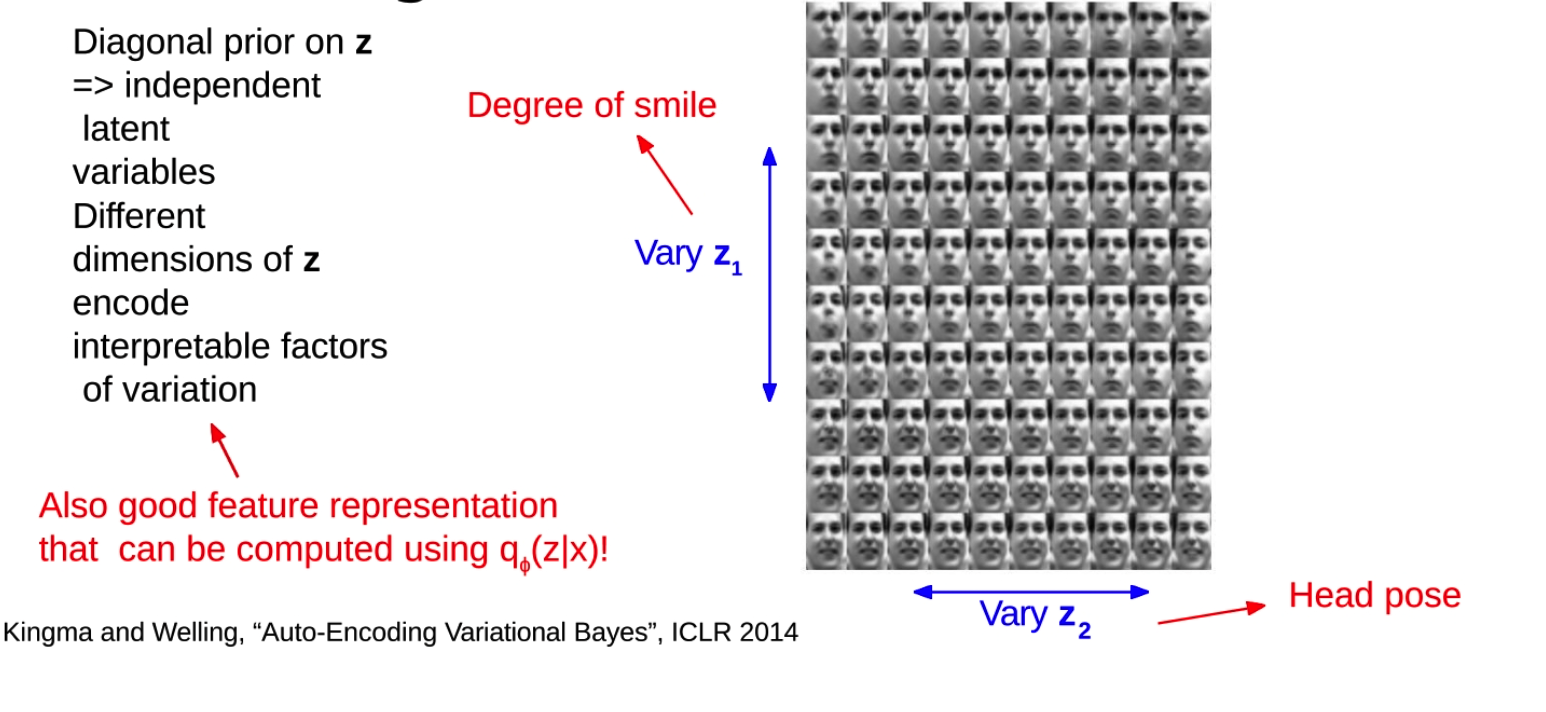
  • VAE的一个重要特性是，不同维度的潜在变量z通常会编码输入数据中的不同因素。**这些因素通常是可以解释的，**也就是说，我们可以理解潜在变量的变化如何影响生成的数据。例如，在处理人脸图像的时候，可能有一个潜在变量控制微笑的程度，另一个潜在变量控制头部的姿势。

  • 当我们从先验分布中采样潜在变量z，并且在一些维度上改变z的值，我们就可以观察到生成的数据如何变化。这可以帮助我们理解我们的模型学到了什么，以及潜在变量如何编码输入数据中的信息。

  • 最后，由于编码器网络可以将输入数据映射到潜在空间，所以我们也可以使用VAE作为一种特征表示学习的方法。这意味着，我们可以将训练好的编码器网络用于其他任务，例如分类或者聚类，这可以帮助我们更好地利用无标签数据。

diffusion models

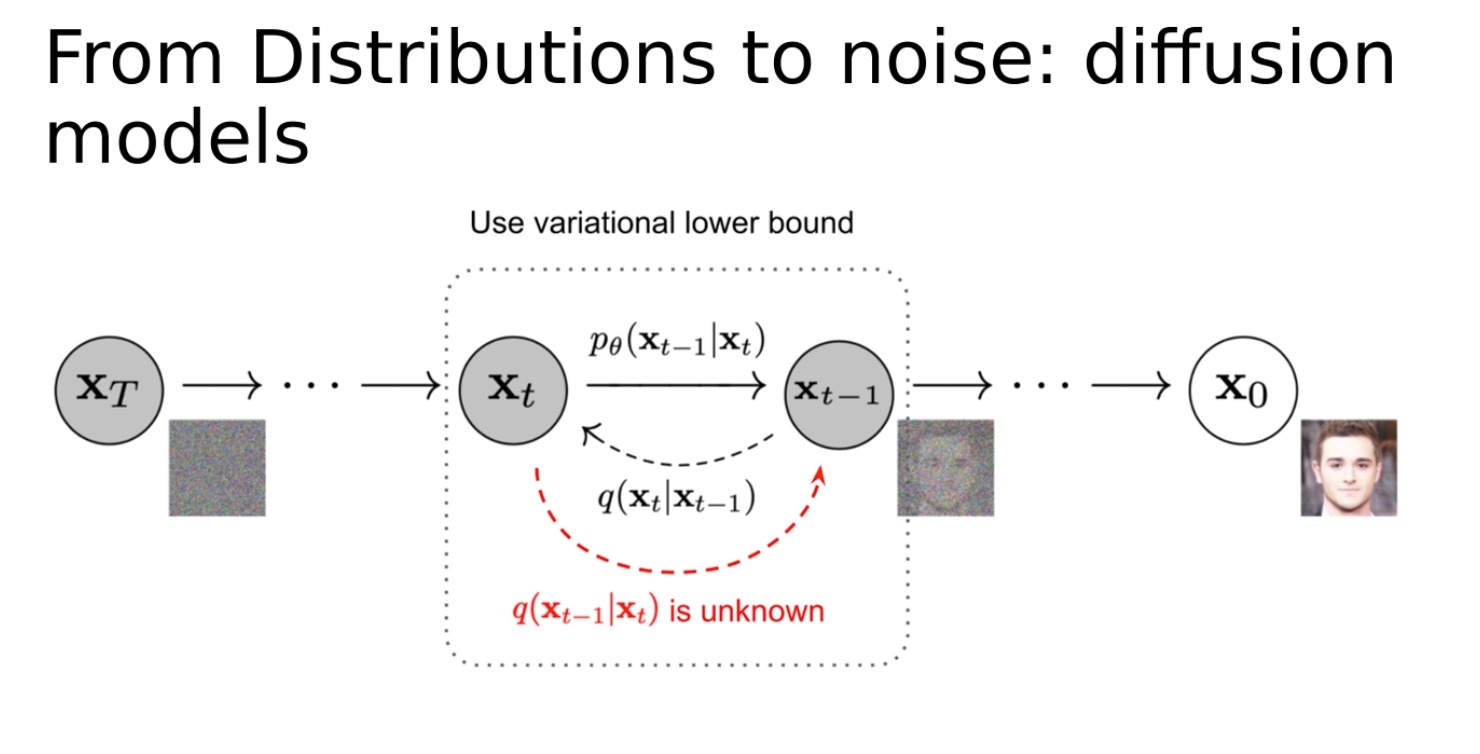
从分布到噪声：扩散模型。这是一种不同的生成模型方法，该方法将生成数据的问题建模为一个扩散过程。在这个过程中，我们开始时有一些随机噪声，然后逐渐改变这个噪声，直到它变成我们想要生成的数据。这个过程可以看作是从最初的噪声分布到目标数据分布的连续变化。

Pros&Cons

• 优点：

  1. 对生成模型的原则性方法：VAE使用了概率模型，它基于最大化数据似然的原则来学习模型参数。

  2. 允许推断$q(z|x)$：VAE训练过程中的编码器部分可以作为一种特征表示学习的方法，这可以用于其他任务，例如分类或聚类。

• 缺点：

  1. 最大化似然的下界：VAE的目标函数是似然的一个下界，而不是似然本身。这意味着VAE的训练可能不会完全优化数据似然，因此在一些任务上可能不如直接优化似然的方法表现好。

  2. 生成的样本质量较低：相比于其他一些生成模型方法（如生成对抗网络，GANs），VAE生成的样本质量通常较低，比如更模糊。

• 目前VAE的一些研究热点

  • 包括更丰富的近似后验分布（例如混合高斯模型，GMMs）和在潜在变量中加入更多结构（例如类别分布）。

Train using a second network: GANs

具体参考我以前写的博客：生成模型（自编码器、VAE、GAN）