1. 原理概述
众所周知,常用的特征维度降维方法有主成分分析,因子分析法,平均值影响法。而平均影响值算法(MIV)是神经网络对输入变量进行降维的最好方法之一。
在神经网络模型实际应用中,由于没有明确的理论来确定输入变量,即网络输入神经元难以确定。假如在神经网络的输入变量中掺杂一些不重要的自变量,不仅会增加模型的训练时间,也会降低模型准确性。因此筛选出影响程度大的网络输入变量对神经网络的改进具有重要意义。
平均影响值(MIV)是评估输入自变量对输出变量影响程度的一个指标,MIV的正负表示该自变量对输出变量的影响方向,其绝对值大小表示影响程度。MIV通过对自变量特征指标值进行加减10%,构建两个新的训练样本,计算其对输出的影响变化值(IV),然后将影响变化值(IV)平均得到该自变量的MIV值,最后将每个自变量都重复上述步骤得到每个自变量的MIV值,并按绝对值大小对各自变量的影响程度进行排序。
2. 实验部分
以西储大学轴承数据为例,计算轴承数据的均值,方差,峰值,峭度,有效值,峰值因子,脉冲因子,波形因子,裕度因子共九个指标作为神经网络的输入神经元。通过MIV值计算,筛选出特征重要度重要的几个指标,达到特征降维,提升诊断精度的目的。
代码实现的功能有很多,包含原生数据的滑动窗口处理,特征值计算,神经网络数据准备,MIV值计算,以及特征筛选后的诊断结果。大家按需所取,如果感觉代码臃肿的后台可以留言,我可以将代码分开再发几篇文章供大家参考。
先上代码结果:
MIV值计算结果:
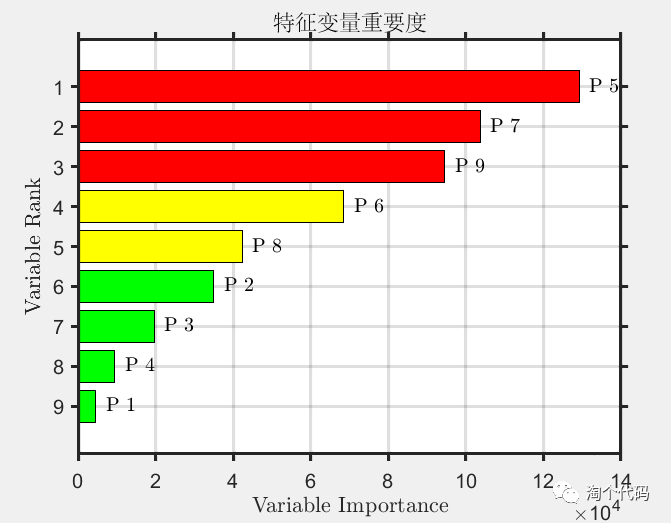
筛选后的前四个重要的特征作为神经网络的神经元输入,带入神经网络后的结果如下:

接下来上正餐:
首先是滑动窗口数据处理代码,一共是10个状态,每个状态有120组样本,每个样本的数据量大小为:1×2048,共选取了电机转速为1797下的10种故障数据来来进行实验。将数据集合在一个data变量中。
clear
clc
addpath(genpath(pwd));
%DE是驱动端数据 FE是风扇端数据 BA是加速度数据 选择其中一个就行
load 97.mat %正常
load 105.mat %直径0.007英寸,转速为1797时的 内圈故障
load 118.mat %直径0.007,转速为1797时的 滚动体故障
load 130.mat %直径0.007,转速为1797时的 外圈故障
load 169.mat %直径0.014英寸,转速为1797时的 内圈故障
load 185.mat %直径0.014英寸,转速为1797时的 滚动体故障
load 197.mat %直径0.014英寸,转速为1797时的 外圈故障
load 209.mat %直径0.021英寸,转速为1797时的 内圈故障
load 222.mat %直径0.021英寸,转速为1797时的 滚动体故障
load 234.mat %直径0.021英寸,转速为1797时的 外圈故障
% 一共是10个状态,每个状态有120组样本,每个样本的数据量大小为:1×2048
w=1000; % w是滑动窗口的大小1000
s=2048; % 每个故障表示有2048个故障点
m = 120; %每种故障有120个样本
D0=[];
for i =1:m
D0 = [D0,X097_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D0 = D0';
D1=[];
for i =1:m
D1 = [D1,X105_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D1 = D1';
D2=[];
for i =1:m
D2 = [D2,X118_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D2 = D2';
D3=[];
for i =1:m
D3 = [D3,X130_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D3 = D3';
D4=[];
for i =1:m
D4 = [D4,X169_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D4 = D4';
D5=[];
for i =1:m
D5 = [D5,X185_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D5 = D5';
D6=[];
for i =1:m
D6 = [D6,X197_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D6 = D6';
D7=[];
for i =1:m
D7 = [D7,X209_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D7 = D7';
D8=[];
for i =1:m
D8 = [D8,X222_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D8 = D8';
D9=[];
for i =1:m
D9 = [D9,X234_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D9 = D9';
data = [D0;D1;D2;D3;D4;D5;D6;D7;D8;D9];然后将data变量的每一条数据求均值,方差,峰值,峭度,有效值,峰值因子,脉冲因子,波形因子,裕度因子共九个指标,并存放在new_data变量中。
for i = 1:size(data,1)
xdata = data(i,:);
junzhi=mean(xdata); %均值
fangcha=mean((xdata-junzhi).^2); %方差
p=max(xdata)-min(xdata); %峰值
k=kurtosis(xdata); %峭度
r=rms(xdata); %有效值
c=p/r; %峰值因子
v=p/mean(abs(xdata)); %脉冲因子
s=r/mean(abs(xdata)); %波形因子
ma=p/mean(sqrt(abs(xdata)))^2; %裕度因子
new_data(i,:) = [junzhi,fangcha,p,k,r,c,v,s,ma];
end接下来是数据送入神经网络之前的整理,具体就是给每类数据打上标签和归一化。
%% 导入数据
bv = 120; %每种状态数据有60组
% 加标签值
hhh = size(new_data,2);
for i=1:size(new_data,1)/bv
new_data(1+bv*(i-1):bv*i,hhh+1)=i;
end
% 输入数据
input=new_data(:,1:end-1); %第1列至倒数第2列为输入
output=data(:,end); %最后1列为输出
[inputn,inputps]=mapminmax(input',0,1);
[outputn,outputps]=mapminmax(output');求取MIV值的具体代码:
p=inputn;
t=outputn;
p=p';
[m,n]=size(p);
yy_temp=p;
% p_increase为增加10%的矩阵 p_decrease为减少10%的矩阵
for i=1:n
p=yy_temp;
pX=p(:,i);
pa=pX*1.1;
p(:,i)=pa;
aa=['p_increase' int2str(i) '=p;'];
eval(aa);
end
for i=1:n
p=yy_temp;
pX=p(:,i);
pa=pX*0.9;
p(:,i)=pa;
aa=['p_decrease' int2str(i) '=p;'];
eval(aa);
end
%% 特征重要度神经网络
nntwarn off;
p=yy_temp;
p=p';
% bp网络建立
net=newff(minmax(p),[8,1],{'tansig','purelin'},'traingdm');
% 初始化网络
net=init(net);
% 网络训练参数设置
net.trainParam.show=50;
net.trainParam.lr=0.05;
net.trainParam.mc=0.7;
net.trainParam.epochs=2000;
net.trainParam.showWindow = false;
net.trainParam.showCommandLine = false;
% 网络训练
net=train(net,p,t);
%% 变量重要度计算
% 转置后sim
for i=1:n
eval(['p_increase',num2str(i),'=transpose(p_increase',num2str(i),');'])
end
for i=1:n
eval(['p_decrease',num2str(i),'=transpose(p_decrease',num2str(i),');'])
end
% result_in为增加10%后的输出 result_de为减少10%后的输出
for i=1:n
eval(['result_in',num2str(i),'=sim(net,','p_increase',num2str(i),');'])
end
for i=1:n
eval(['result_de',num2str(i),'=sim(net,','p_decrease',num2str(i),');'])
end
for i=1:n
eval(['result_in',num2str(i),'=transpose(result_in',num2str(i),');'])
end
for i=1:n
eval(['result_de',num2str(i),'=transpose(result_de',num2str(i),');'])
end
% MIV的值
% MIV被认为是在神经网络中评价变量相关的最好指标之一
% 其符号代表相关的方向,绝对值大小代表影响的相对重要性。
for i=1:n
IV= ['result_in',num2str(i), '-result_de',num2str(i)];
eval(['MIV_',num2str(i) ,'=mean(',IV,')*(1e7)',';']) ;
eval(['MIVX=', 'MIV_',num2str(i),';']);
MIV(i,:)=MIVX;
end
[MB,iranked] = sort(MIV,'descend');数据可视化分析,画图:
%% 数据可视化分析
%-------------------------------------------------------------------------------------
figure()
barh(MIV(iranked),'g');
xlabel('Variable Importance','FontSize',12,'Interpreter','latex');
ylabel('Variable Rank','FontSize',12,'Interpreter','latex');
title('特征变量重要度','fontsize',12,'FontName','华文宋体')
hold on
barh(MIV(iranked(1:5)),'y');
hold on
barh(MIV(iranked(1:3)),'r');
grid on
xt = get(gca,'XTick');
xt_spacing=unique(diff(xt));
xt_spacing=xt_spacing(1);
yt = get(gca,'YTick');
% 条形标注
for ii=1:length(MIV)
text(...
max([0 MIV(iranked(ii))+0.02*max(MIV)]),ii,...
['P ' num2str(iranked(ii))],'Interpreter','latex','FontSize',12);
end
set(gca,'FontSize',12)
set(gca,'YTick',yt);
set(gca,'TickDir','out');
set(gca, 'ydir', 'reverse' )
set(gca,'LineWidth',2);
drawno接下来是将求得的iranked值带入神经网络里边,求出诊断结果的代码。
function [outputt,predict_label] = BP(iranked)
addpath(genpath(pwd));
%DE是驱动端数据 FE是风扇端数据 BA是加速度数据 选择其中一个就行
load 97.mat %正常
load 105.mat %直径0.007英寸,转速为1797时的 内圈故障
load 118.mat %直径0.007,转速为1797时的 滚动体故障
load 130.mat %直径0.007,转速为1797时的 外圈故障
load 169.mat %直径0.014英寸,转速为1797时的 内圈故障
load 185.mat %直径0.014英寸,转速为1797时的 滚动体故障
load 197.mat %直径0.014英寸,转速为1797时的 外圈故障
load 209.mat %直径0.021英寸,转速为1797时的 内圈故障
load 222.mat %直径0.021英寸,转速为1797时的 滚动体故障
load 234.mat %直径0.021英寸,转速为1797时的 外圈故障
% 一共是10个状态,每个状态有120组样本,每个样本的数据量大小为:1×2048
w=1000; % w是滑动窗口的大小1000
s=2048; % 每个故障表示有2048个故障点
m = 120; %每种故障有120个样本
D0=[];
for i =1:m
D0 = [D0,X097_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D0 = D0';
D1=[];
for i =1:m
D1 = [D1,X105_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D1 = D1';
D2=[];
for i =1:m
D2 = [D2,X118_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D2 = D2';
D3=[];
for i =1:m
D3 = [D3,X130_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D3 = D3';
D4=[];
for i =1:m
D4 = [D4,X169_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D4 = D4';
D5=[];
for i =1:m
D5 = [D5,X185_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D5 = D5';
D6=[];
for i =1:m
D6 = [D6,X197_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D6 = D6';
D7=[];
for i =1:m
D7 = [D7,X209_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D7 = D7';
D8=[];
for i =1:m
D8 = [D8,X222_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D8 = D8';
D9=[];
for i =1:m
D9 = [D9,X234_DE_time(1+w*(i-1):w*(i-1)+s)];
end
D9 = D9';
data = [D0;D1;D2;D3;D4;D5;D6;D7;D8;D9];
for i = 1:size(data,1)
xdata = data(i,:);
junzhi=mean(xdata);
fangcha=mean((xdata-junzhi).^2);
p=max(xdata)-min(xdata);
k=kurtosis(xdata);
r=rms(xdata);
c=p/r;
v=p/mean(abs(xdata));
s=r/mean(abs(xdata));
ma=p/mean(sqrt(abs(xdata)))^2;
new_data1(i,:) = [junzhi,fangcha,p,k,r,c,v,s,ma];
end
%这里进行一个简单的判断
iranked = iranked';
if sum(length(iranked)==[1,2,3,4,5,6,7,8,9])==9
new_data = new_data1;
else
ir = iranked(1:4); %取重要度较高的前4个特征作为神经网络的输入
new_data = new_data1(:,ir);
end
rng('default')
%% 导入数据
bv = 120; %每种状态数据有60组
% 加标签值
hhh = size(new_data,2);
for i=1:size(new_data,1)/bv
new_data(1+bv*(i-1):bv*i,hhh+1)=i;
end
new_data=new_data(randperm(size(new_data,1)),:); %此行代码用于打乱原始样本,使训练集测试集随机被抽取,有助于更新预测结果。
input=new_data(:,1:end-1);
output1 =new_data(:,end);
for i=1:size(new_data,1)
switch output1(i)
case 1
output(i,1)=1;
case 2
output(i,2)=1;
case 3
output(i,3)=1;
case 4
output(i,4)=1;
case 5
output(i,5)=1;
case 6
output(i,6)=1;
case 7
output(i,7)=1;
case 8
output(i,8)=1;
case 9
output(i,9)=1;
case 10
output(i,10)=1;
end
end
m=fix(size(new_data,1)*0.7); %训练的样本数目
input_train=input(1:m,:)';
output_train=output(1:m,:)';
input_test=input(m+1:end,:)';
output_test=output(m+1:end,:)';
%% 数据归一化
[inputn,inputps]=mapminmax(input_train,0,1);
% [outputn,outputps]=mapminmax(output_train);
inputn_test=mapminmax('apply',input_test,inputps);
hiddennum_best = 30;
%% 构建最佳隐含层节点的BP神经网络
disp(' ')
disp('标准的BP神经网络:')
net0=newff(inputn,output_train,hiddennum_best,{'tansig','purelin'},'trainlm');% 建立模型
%网络参数配置
net0.trainParam.epochs=1000; % 训练次数,这里设置为1000次
net0.trainParam.lr=0.01; % 学习速率,这里设置为0.01
net0.trainParam.goal=0.000001; % 训练目标最小误差,这里设置为0.0001
net0.trainParam.show=25; % 显示频率,这里设置为每训练25次显示一次
% net0.trainParam.mc=0.01; % 动量因子
net0.trainParam.min_grad=1e-6; % 最小性能梯度
net0.trainParam.max_fail=6; % 最高失败次数
%开始训练
net0=train(net0,inputn,output_train);
%预测
an0=sim(net0,inputn_test); %用训练好的模型进行仿真
predict_label=zeros(1,size(an0,2));
for i=1:size(an0,2)
predict_label(i)=find(an0(:,i)==max(an0(:,i)));
end
outputt=zeros(1,size(output_test,2));
for i=1:size(output_test,2)
outputt(i)=find(output_test(:,i)==max(output_test(:,i)));
end
%% 画方框图
confMat = confusionmat(outputt,predict_label); %output_test是真实值标签
figure;
set(gcf,'unit','centimeters','position',[15 5 13 9])
plotConfMat(confMat.');
xlabel('Predicted label')
ylabel('Real label')
hold off
end欢迎大家评论区留言哦!