目录

Linux之文件一般权限

文件和目录的一般权限

 解析：

 文件类型

 文件的权限针对三类对象进行定义

文件针对每类访问者定义的三种权限

对于文件和目录，r，w，x的作用以及含义

设置文件和目录的一般权限

修改文件或目录权限 --- chmod（change mode）命令

        语法格式

        参数及作用

        权限值的表示方法

                方法一 --- 使用3位的八进制数表示

                方法二 --- 使用字符串表示

                        语法格式

                        案例

修改文件或目录的属主和属组 --- chown（change owner）命令

        修改文件或目录的拥有者

                语法格式

                参数及作用

                案例

        修改文件或目录的属组

                语法格式

                案例

---

Linux之文件一般权限

文件和目录的一般权限

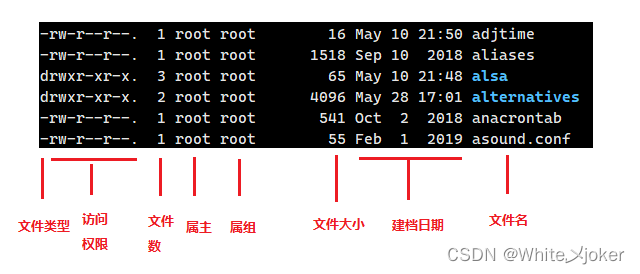
 解析：

        第一个字符 --- 表示改文件的类型，其类型标识符和对应的文件类型

        第2~4个字符 --- 表示该文件的属主用户(文件的所有者)对该文件的访问权限

        第5~7个字符 --- 表示改文件的属组用户(与属主用户同组的各成员用户)对改文件的访问权限

        第8~10个字符 --- 表示其他所有用户对该文件的访问权限

        第11个字符 --- 用来标识四否有一个可替换的访问控制措施应用在改文件上。当为一个空格时，表示系统没有可替换的访问控制措施；当为“.”字符时，代表该文件使用了SELinux安全上下文；当为“+”字符时，表示该文件在使用SElinux安全上下文的同时，还混用其他访问控制措施（如：访问控制列表ACL）   

 文件类型

 

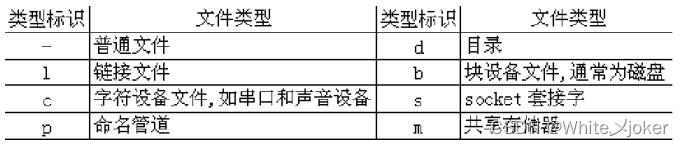
 文件的权限针对三类对象进行定义

        owner 属主，缩写u

        group 属组，缩写g

        other 其他，缩写o

文件针对每类访问者定义的三种权限

        r --- read读

        w --- write 写

        x --- eXecute 执行

        另 X --- 针对目录加执行权限，文件不加执行权限（因为文件具备执行权限有安全隐患）

注意：

        root账户不受文件权限的读写限制，执行权限受限制

对于文件和目录，r，w，x的作用以及含义

权限	对文件的影响	对目录的影响
r（读取）	可以读取文件的内容	可以列出目录的内容（文件名）
w（写入）	可以更改文件的内容	可以创建或删除目录中的任意文件
x（可执行）	可以作为命令执行文件	可以访问目录的内容（取决于目录中文件的权限）

权限项	文件类型	读	写	执行	读	写	执行	读	写	执行
字符表示	(d|l|c|s|p)	(r)	(w)	(x)	(r)	(w)	(x)	(r)	(w)	(x)
数字表示		4	2	1	4	2	1	4	2	1
权限分配		文件所有者			文件所属组用户			文件其他用户

设置文件和目录的一般权限

修改文件或目录权限 --- chmod（change mode）命令

语法格式

        chmod [-选项] [ugoa] [+-=] [rwx] 文件或目录...

        chmod [-选项] nnn 文件或目录...

解析：

        ugoa --- 表示权限设置所针对的用户类别，可以使其中字母中的一个或组合。u（user）表示文件或目录的属主（所有者）；g（group）表示属组内的用户；o（others）表示其他任何用户；a（all）表示所用用户（即u+g+o）。

        +|-|= --- 表示设置权限的操作动作，+表示添加某个权限；-表示取消某个权限；=表示只赋予给定的权限，并取消原有的权限

        rwx --- 用字符形式表示的所设置的权限，可以使其中字母中的一个或组合

        nnn --- 用三位八进制数字表示的所设置的权限

参数及作用

参数	作用
-R	递归修改指定目录下的所有文件、子目录的权限

权限值的表示方法

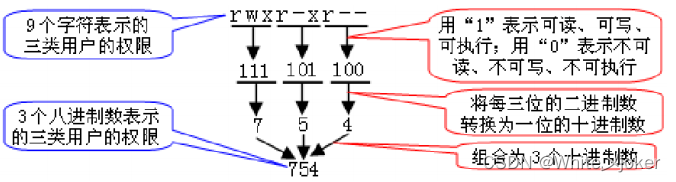
方法一 --- 使用3位的八进制数表示

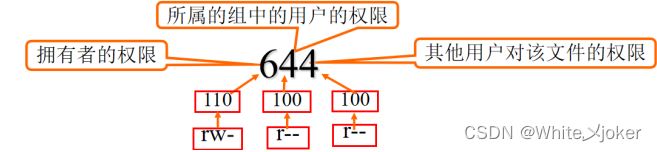
方法二 --- 使用字符串表示

语法格式

        chmod [-R] {[ugoa][+-=][rwxst]} <文件名或目录名>

         chmod [-R] 用户对象+|-|=权限符

用户对象
u	拥有者
g	拥有者所属的用户组
o	其他用户
a	所有的
+	增加某项权限
.	去掉某项权限
=	赋予某项权限
权限符	r、w、x、s

案例

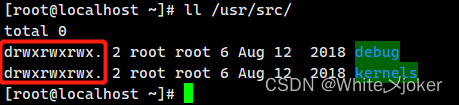
        示例 --- 将目录/usr/src及其下面的所有子目录和文件的权限改为所有用户对其都有读、写权限

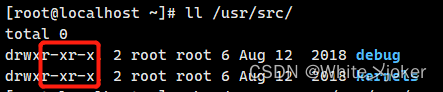
[root@localhost ~]# chmod -R a+rw /usr/src/

修改文件或目录的属主和属组 --- chown（change owner）命令

修改文件或目录的拥有者

语法格式

        chown [-选项] 新属主[:[新属组]] 被改变归属的文件或目录

注意：

        用空格分隔列表中多个文件名或目录名

参数及作用

参数	作用
-R	可递归设置指定目录下的全部文件（包括子目录和子目录中的文件）的所属关系。

案例

        示例 --- 将/test/file1.txt文件的属主改为zhang3用户、属组改为li4用户

[root@localhost ~]# chown zhang3:li4 /test/file1.txt 

修改文件或目录的属组

语法格式

        chown [-选项] :新属组 被改变归属的文件或目录

        其他命令 --- chgrp [-选项] 新属组 被改变归属的文件或目录

案例

        示例 --- 将/test/file1.txt文件的属组改为zhang3用户