1、无限分割计算圆的面积

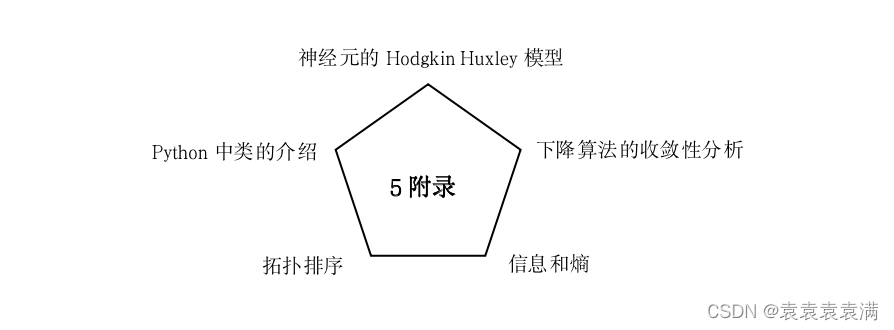
        考虑将圆切成若干等份，下图为4等份。

        下图为8等份。 

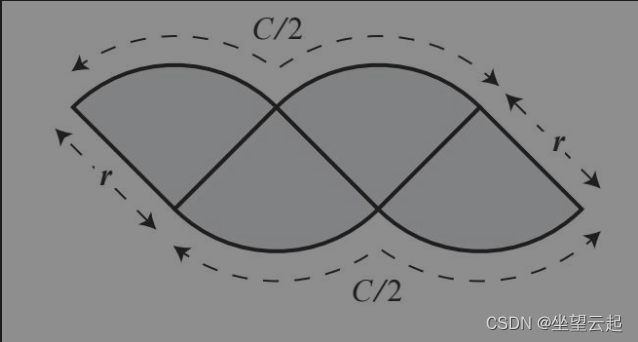
        下图为16等份。 

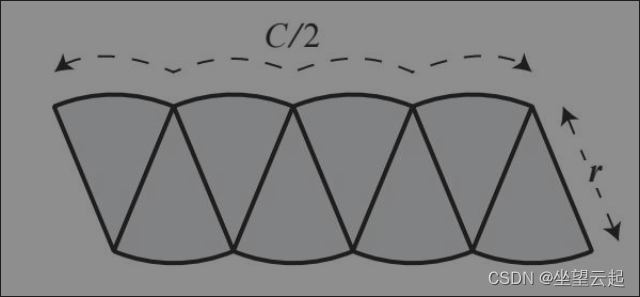
        下图为最终想象出来的极限矩形，据此分割为无穷等份的圆拼接为一个矩形。

        矩形的面积 = r * C / 2。 r为半径，C为周长。

2、夹逼法计算圆周率

         借助圆内接96边形和圆外接96边形，阿基米德最终证明π大于3+10/71而小于3+10/70。

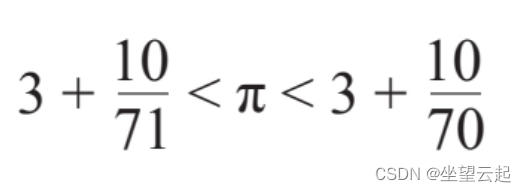
        250年前后，中国几何学家刘徽改进了阿基米德计算圆周率的 方法。两个世纪后，祖冲之将刘徽的方法应用于24576边形，并通过绝对称得上壮举的计算，把圆周率的虎钳收紧到8位数： 

3.141 592 6＜π＜3.141 592 7

3、求解抛物线弓形的面积

         阿基米德想象将弓形底部的斜线 向上滑动，同时与它自身保持平行，直到它刚好触碰到抛物线顶部附 近的某个点。这个特殊的接触点被称为切点，它确定了大三角形的第三个角的 位置，另外两个角的顶点就是斜线与抛物线的交点。

        阿基米德调用关于抛物线和三角形的已知几何事实，将相邻的层级联系起来。他证明了每个新构建三角形的面积都是上一层级三角形面积的1/8，因此，如果我们说第一层级的三角形占据了一个面积单位（这个三角形将充当我们的面积标准），那么第二层级的两个三角形一共占据了1/8+1/8=1/4个面积单位。

         将无穷个层级的三角形碎 片重新组合在一起，就可以得出抛物线弓形的面积S

         将上述无穷级数中的 每一项都乘以4，就会得到如下。

         神奇的事情发生了。4×S=4+S，既3×S=4。抛物线弓形的面积是大三角形面积的4/3。

4、行李箱的优化问题

        假设你想设计一个矩形的箱子来存放尽可能多的物品，但要满足两个约束条件。第一，这个箱子必须有一个正方形的横截面，宽x英寸，深x英寸。第二，它必须能放进某家航空公司的机舱行李架。根据航空公司对随身携带行李的规定，箱子的宽度、深度和高度之和不能超过45英寸。那么，当x是多少英寸时，箱子的容积最大呢？

        和解决大多数代数问题一样，我们先要把所有给定的信息转化成 符号。由于箱子的宽度和深度都是x，加起来就是2x。而且，箱子的高 度、宽度和深度之和不能超过45英寸，所以它的高度是45–2x。那 么 ， 箱 子 的 容 积 是 x×x×(45–2x)=45x 2–2x 3 ， 我 们 将 其 表 示 成 V(x)：

        如果我们以x为横轴、V(x)为纵轴，用计算机或绘图计算器画出图 像，就会看到这条曲线先上升，并像预期的那样在x=15英寸时达到最 大值，然后下降直至0x。

         我们可以用现在熟悉的微分学方法找出最大值，即求 V(x)的导数并使其等于0。求解过程如下。

          但是，费马没有绘图计算器或计算机，也没有导数的概念。那 么，他是如何解决这个问题的呢？他利用了最大值的一个特性，即低于最大值的水平线都和曲线相交于两个点，如图所示。

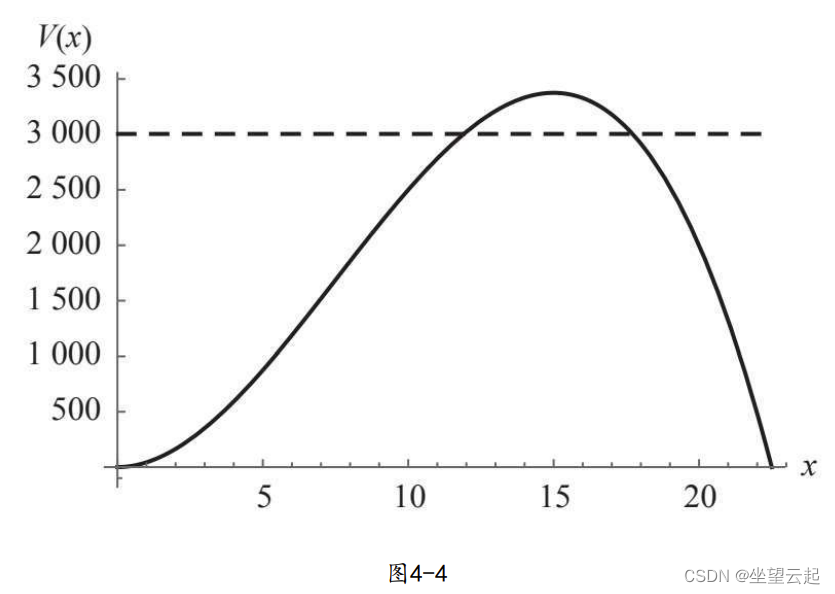
        在最大值处，这两个点发生碰撞。寻找碰撞点就是费马确定最大 值的方法，换言之，他需要推导出两点合并为一点（形成“重交 点”）的条件。有了正确的思路，余下的就是代数运算（符号处理） 了。具体过程如下：

        假设两个交点处的x分别为a和b，它们位于同一条水平线上，所以 V(a)=V(b)，依次计算。

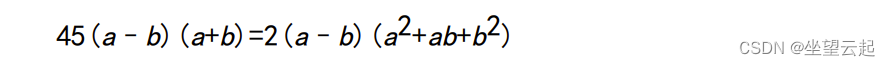
         费马先是假设a和b不相 等，但他又假设当a和b在最大值处合并且相等时，他之前推导出的方 程仍然成立。总之，他令a≈b，并大胆地用a替换上述方程中的b得到：

        上式进一步化简为，它的解是a=0和a=15。 

        费马的思维方式很有趣，因为它不仅简洁易懂，而且独特新奇。