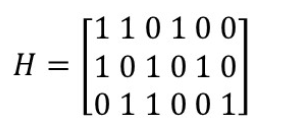本专栏包含信息论与编码的核心知识，按知识点组织，可作为教学或学习的参考。markdown版本已归档至【Github仓库：https://github.com/timerring/information-theory 】或者公众号【AIShareLab】回复 信息论 获取。

线性分组码

基本概念

线性分组码数学定义: 编码前信息码元空间 $U^k$ , 经映射 $f$ , 编码后码字空间 $C^n$ , 即 $f:U^k\to C^n$ , 其中 $n>k$ 。 若 $f$ 进一步满足线性关系:
$$f\left(\alpha \mathbf{u}\oplus \beta {\mathbf{u}}^{\prime }\right)=\alpha f(\mathbf{u})\oplus \beta f\left({\mathbf{u}}^{\prime }\right)$$
其中 α , β ∈ G F ( 2 ) = { 0 , 1 } , u 与 u ′ ∈ U k \alpha, \beta \in G F(2)=\{0,1\}, \mathbf{u} 与 \mathbf{u}^{\prime} \in \mathbf{U}^{k} α,β∈GF(2)={0,1},u与u′∈Uk 则称 $f$ 为线性编码映射，进一步若 f 为一一对应映射，则 f 为唯一可译线性编码 。由 f 编写成的码 c 称为线性分组码。

线性分组码是一类奇偶校验码，它由（n，k ）形式表示。编码器将一个 k 比特信息分组（信息矢量）转变成一个更长的由给定符号集组成的 n 比特编码分组（编码矢量）。当这个符号集包含 2 个元素 (0 and1） 时 , 称为二进制编码。

kbit 信息形成 $2^k$ 不同的信息序列 , 称为 k 元组。 nbit 可以形成 $2^n$ 个不同序列，称为 n 元组 。（n, k ）分组码输出的长度为 n 的序列称为码字。所有这些码字的集合称为该线性分组码的码组。

定义: 如果分组码中任意两个码字的线性组合仍是分组码的一个码字，那么该分组码是线性的。 对于二进制码，如果 $c_i$ 和 $c_j$是码字，$c_i$+$c_j$也是码字。其中+表示按位模 2 加 (就是逐位相加)。

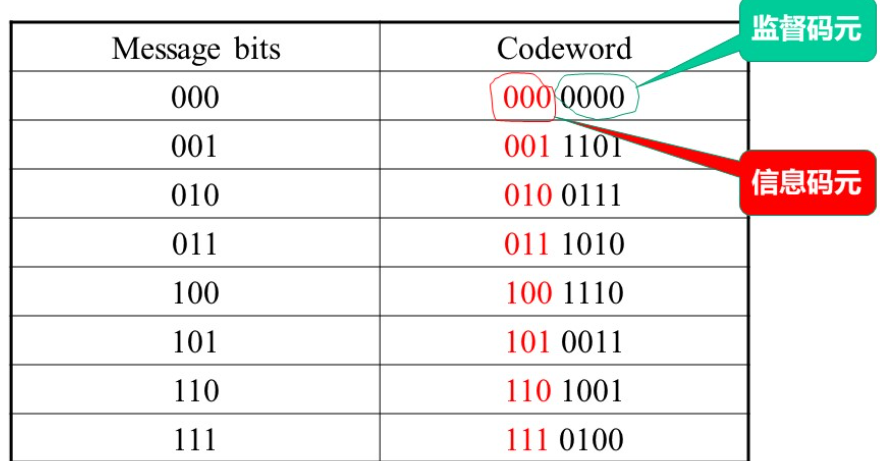
例:(7,3)线性分组码

$d_{\min }=4$ . $c_i+c_j$ 仍为码字

快速计算方法：看除全零码以外，最小的码重就是它的码距。

编码-生成矩阵

编码和生成矩阵

（n，k ）线性分组码的构造——依据给定的 k 个信息码元，设计满足编码条件（最小码距、码率）的 n-k个监督码元。

例: 二元 (7,3) 线性分组码, n=7, k=3, r=7-3=4 ,

$$\mathbf{u}=\left(u_2,u_1,u_0\right)\to \mathbf{c}=\left(c_6,c_5,c_4,c_3,c_2,c_1,c_0\right)$$
构造:

编码位高位直接对应信息位;

编码位低位由信息位组合而成。.
$$\begin{array}{ll}{c}_6=u_2& c_3=u_2⨁u_0=c_6\oplus c_4\\ c_5=u_1& c_2=u_2⨁u_1\oplus u_0=c_6\oplus c_5\oplus c_4\\ c_4=u_0& c_1=u_2⨁u_1=c_6\oplus c_5\\ & c_0=u_1\oplus u_0=c_5\oplus c_4\end{array}$$
写成矩阵形式，为

即 : $\mathbf{C}=\mathbf{uG}$
设信息码元序列为 $\mathbf{u}$ , 长度为 k , 由 $\mathbf{C}=\mathbf{uG}$ 可以得到一个 n 位的码组, 也即由 k 个信息位经过一个线性变换矩阵 $\mathbf{G}$ 产生。

$\mathbf{G}$- 生成矩阵
$$\mathbf{G}=\left(\begin{array}{c}{\mathbf{g}}_1\\ {\mathbf{g}}_2\\ ⋮\\ {\mathbf{g}}_k\end{array}\right)=\left(\begin{array}{ccc}{g}_{11}& \dots & g_{1n}\\ ⋮& ⋮& ⋮\\ g_{k1}& \dots & g_{kn}\end{array}\right)k\times n\text{ 阶 }$$
线性分组码的编码: $\mathrm{C}=\mathbf{u G} $

该 (7,3) 码的生成矩阵为

如：若输入的信息为 [011], 由 $\mathrm{C}=\mathrm{uG}$ , 得$\mathrm{C}=[0111010]$, 和码表中的码字一致。

例 生成矩阵如图矩阵。
若信息为 $\mu =\left(\begin{array}{lll}1& 1& 1\end{array}\right)$ ，则编码出的码字是什么? 1110100
$$G=\left[\begin{array}{lllllll}1& 0& 0& 1& 1& 1& 0\\ 0& 1& 0& 0& 1& 1& 1\\ 0& 0& 1& 1& 1& 0& 1\end{array}\right]$$

系统码与非系统码

若生成矩阵可以分解成两个子块,
$$\mathbf{G}=[\mathbf{I}⋮\mathbf{Q}]\text{ 或 }\mathbf{G}=[\mathbf{Q}⋮\mathbf{I}]$$
其中 $\mathrm{I}$ 为 $\mathbf{k}$ 阶单位矩阵, $\mathrm{Q}$ 为 $\mathbf{k}\ast (\mathbf{n}-\mathbf{k})$ 阶矩阵, 则 C 为系统码，又称为组织码, G 为系统码的生成矩阵 (典型生成矩阵)。

若信息分组以不变的形式出现在线性分组码的任意k位(一般为前k位，或后k位），则称此码组为系统码，否则称为非系统码。(如果编码器输出的比特流中原样包含了信息比特，叫系统码。编码输出中的这些原始信息位也叫系统位。)

生成矩阵的特性

a. 生成矩阵 $\mathbf{G}$ 一定是 $\mathbf{k}$ 行 $\mathbf{n}$ 列的 $\mathbf{k}\times \mathbf{n}$ 阶矩阵, $\mathrm{G}$ 的每行构成一行矢量, 共有 $\mathbf{k}$ 个矢量。

b. 线性分组码的每个码字是生成矩阵 $\mathbf{G}$ 各行矢量的线性组合。
$$\begin{array}{r}\mathbf{C}=\mathbf{uG}=\left(u_{k-1},\dots ,u_1,u_0\right)\left(\begin{array}{c}{\mathbf{g}}_1\\ {\mathbf{g}}_2\\ ⋮\\ {\mathbf{g}}_k\end{array}\right)\\ =u_{k-1}{\mathbf{g}}_1+u_{k-2}{\mathbf{g}}_2+\dots +u_1{\mathbf{g}}_{k-1}+u_0{\mathbf{g}}_k\end{array}$$

c. G的每一行是一个码字。

d. 生成矩阵G的各行线性无关。思考:已知码字集合，如何构造生成矩阵?

e. 对非系统码的生成矩阵，总可以经过初等行变换及列交换构造成另一等价的系统码的生成矩阵并且这两个线性分组码检、纠错性能相同。

求非系统 (7,4) 线性分组码的等价系统码生成矩阵。
$$\mathrm{G}=\left[\begin{array}{lllllll}0& 1& 0& 1& 0& 1& 0\\ 0& 1& 1& 1& 0& 0& 1\\ 1& 1& 1& 0& 0& 1& 0\\ 1& 0& 1& 0& 1& 0& 1\end{array}\right]$$

列的交换和初等行变换不改变矩阵的秩，变换后矩阵的各行矢量仍线性无关。

任何一个线性分组 (n, k)码都可等价于一个系统码。（纠错能力、编码结构)

思考:由非系统型生成矩阵变换成系统型生成矩阵，答案唯一吗?

已知某(7，4)分组码的码表如下，请问最小汉明距是多少?请写出该码的典型生成矩阵。

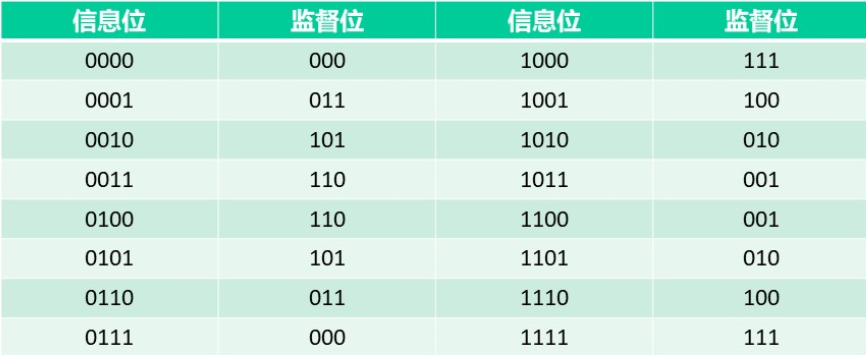
最小汉明距：3

生成矩阵:
$$G=\left[\begin{array}{lllllll}1& 0& 0& 0& 1& 1& 1\\ 0& 1& 0& 0& 1& 1& 0\\ 0& 0& 1& 0& 1& 0& 1\\ 0& 0& 0& 1& 0& 1& 1\end{array}\right]$$

检错-监督矩阵

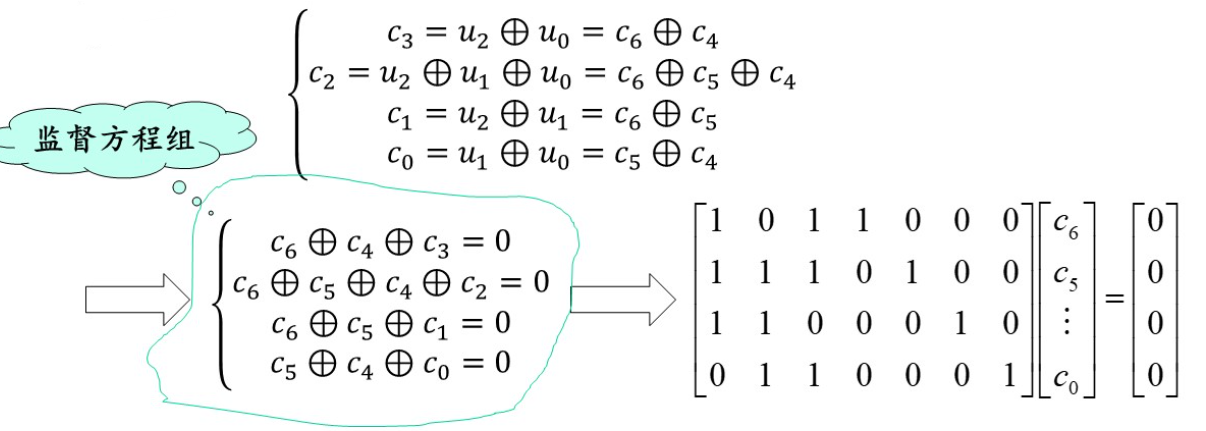
由分组码的生成矩阵可得到其监督矩阵。

$${\mathbf{HC}}^T=0^T,[\mathbf{P}:\mathbf{I}]{\mathbf{C}}^T=0^T$$
一般情况下, 一个 (n, k) 线性分组码的H矩阵中的（n-k）行对应（n-k）个线性监督方程组, 以确定（n-k）个监督码元。

$\mathbf{H}$——线性分组码的监督矩阵，是$（n-k）\times \mathbf{n}$ 阶的。

若 H=[P ：I], 其中 I 是 ( n-k ）阶方阵, 则 H 为典型监督矩阵。

监督矩阵
$$H\cdot C^T=H\cdot G^T{\mu }^T=0^T$$
或者 $\mathbf{G}$ 每一行及其线性组合都是 (n, k) 码的码字, 故 $H\cdot G^T=0^T\Rightarrow G\cdot H^T=0$ .
$$\begin{array}{c}G\cdot H^T=[\begin{array}{ll}I& Q\end{array}\left[\begin{array}{c}{P}^T\\ I\end{array}\right]=P^T+Q=0\\ \therefore Q=P^T\text{ 或 }P=Q^T\end{array}$$
请思考：已知 $\mathbf{G}=[I:Q]\Rightarrow \mathbf{H}=[\mathrm{P}:I]$ 若 $G=[Q:I]$ ，则 $H=[I:P]$

监督方程

由
$$\begin{array}{rl}H\cdot C^T& =H\cdot G^T{\mu }^T=0^T\\ & \Rightarrow C{H}^T=0\end{array}$$
可知，若
$$\tilde{\mathbf{C}}{\mathbf{H}}^T\ne 0$$
则 $\tilde{\mathbf{C}}$ 不是有效码字, 从而检测出错误。 故：
$${\mathbf{CH}}^T=0$$
称为线性分组码的监督方程。

监督矩阵的特性

• 由H矩阵可以建立线性分组码的线性方程组, H矩阵共有 n-k 行, 其中每行代表一个线性方程的系数, 表示求一个监督位的线性方程;
• H矩阵的每行与码集中的一个码字的内积为 0 ;
• 任何一个 $ (\boldsymbol{n}-\boldsymbol{k})$ 线性分组码的 $\mathrm{H}$ 矩阵有 $ (\boldsymbol{n}-\boldsymbol{k})$ 行, 且每行线性无关;
• 一个 $(\mathbf{n},\mathbf{k},d)$ 线性分组码, 如要纠正小于等于 t 个错误, 则其充要条件是H矩阵中任何 2t 列线性无关, 由于最小距离 d=2t+1 , 所以也相当于要求 H 矩阵中任意 (d-1) 列线性无关。
• 系统码的典型生成矩阵 $\mathbf{G}$ 可以方便的得到典型监督矩阵 $\mathbf{H}$ 。

已知一 (6,3) 线性分组码的生成矩阵G如下，求其监督矩阵 $\mathbf{H}$ 。
$$\begin{array}{l}\mathbf{G}=\left[\begin{array}{llllll}1& 0& 0& 1& 1& 0\\ 0& 1& 0& 1& 0& 1\\ 0& 0& 1& 0& 1& 1\end{array}\right]\end{array}$$

参考文献：

1. Proakis, John G., et al. Communication systems engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
2. Proakis, John G., et al. SOLUTIONS MANUAL Communication Systems Engineering. Vol. 2. New Jersey: Prentice Hall, 1994.
3. 周炯槃. 通信原理（第3版）[M]. 北京：北京邮电大学出版社, 2008.
4. 樊昌信, 曹丽娜. 通信原理（第7版） [M]. 北京：国防工业出版社, 2012.