一、TSP问题简介

旅行推销员问题(TSP)提出以下问题：“给定 $n$ 个城市的列表，其中有一个起始城市，以及每对城市之间的距离，访问每个城市一次并返回起始城市的最短可能路线是什么？”。

这又是一个重要的NP-hard组合优化，特别是在运筹学和理论计算机科学领域。这个问题最早是在1930年提出的，是离散最优化中研究最深入的问题之一。

二、数学建模

让我们考虑一组 $n$ 个城市，其中每个城市 $i$ 具有坐标 $x_i,y_i),i = 1,2,...,n$ 。

在这种情况下，状态空间的每个点 $X$ 必须代表我们访问 $n$ 个城市的顺序中的一个可能的排列。

为简单起见，我们考虑使用字典顺序的构造初始解决方案：

在这里插入图片描述
目标函数评估在于计算对应于任意向量 $X$ 的旅程的长度 $f$ ：

$f(X)=\sum_{i=1}^{n-1} d\left(X_i, X_{i+1}\right)+d\left(X_N, X_1\right)$

其中， $X_i$ 是 $X$ 的第 $i$ 个元素，如果 $X_i = k，X_{i+1} = l$ ，则城市 $k$ 城市 $l$ 的欧式距离为：

$d_1\left(X_i, X_{i+1}\right)=\sqrt{\left(x_l-x_k\right)^2+\left(y_l-y_k\right)^2}$

城市 $k$ 城市 $l$ 的伪欧式距离为：

$d_2\left(X_i, X_{i+1}\right)=\sqrt{\frac{\left(x_l-x_k\right)^2+\left(y_l-y_k\right)^2}{10}}$

注意，在 $f$ 的上述定义中，最后一项 $d(X_N,X_1)$ 表示返回起始城市的旅程的最后一段。

众所周知，与旅行推销员问题相关联的复杂性远高于背包问题。对于一个有 $n$ 个城市的问题，要考虑的潜在旅行次数是 $n!$ ，它随 $n$ 的增长速度比 $2^n$ 快得多：

在这里插入图片描述
为了说明问题的复杂性，如果目标函数的一次评估需要 $109$ 秒，那么评估每个可能解决方案的简单枚举算法将需要以下CPU时间：

在这里插入图片描述

三、实现细节

有关自适应大邻域搜索算法的详细介绍请看：【运筹优化】元启发式算法详解：(自适应)大邻域搜索算法（( Adaptive) Large Neighborhood Search，(A)LNS）+ 案例讲解&代码实现

我实现了三个销毁算子和三个修复算子分别如下：

销毁算子1：随机删除k个城市
销毁算子2：随机删除序列中的一个片段
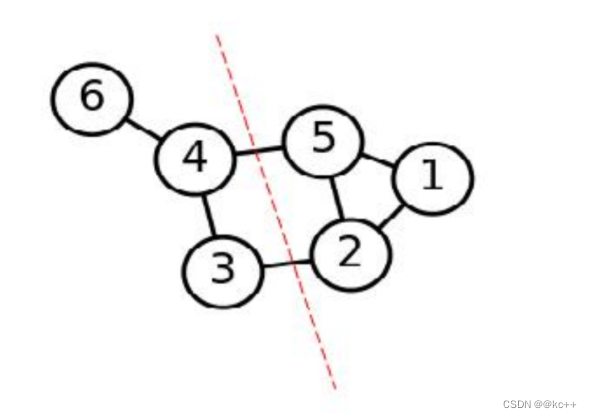
销毁算子3：破坏一对交叉的边

修复算子1：随机插入修复
修复算子2：启发式插入修复
修复算子3：直接接到部分序列的后面

交换两个元素可以使用位运算，例如想交换 a 和 b，可以采用下面的代码：

b = a ^ b;
a = a ^ b;
b = a ^ b;

注意：此方法只是减少了中间变量的使用，降低了内存消耗，并不能提升性能

四、案例实战

本案例的所有数据和代码均上传至 GitHub 仓库：https://github.com/WSKH0929/MetaHeuristics

4.1 测试案例说明

使用的是tsplib上的数据att48，这是一个对称TSP问题，城市规模为48，其最优值为10628（取整的伪欧氏距离）

tsplib地址：http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/tsp/

下面是att48的文件内容：

NAME : att48
COMMENT : 48 capitals of the US (Padberg/Rinaldi)
TYPE : TSP
DIMENSION : 48
EDGE_WEIGHT_TYPE : ATT
NODE_COORD_SECTION
1 6734 1453
2 2233 10
3 5530 1424
4 401 841
5 3082 1644
6 7608 4458
7 7573 3716
8 7265 1268
9 6898 1885
10 1112 2049
11 5468 2606
12 5989 2873
13 4706 2674
14 4612 2035
15 6347 2683
16 6107 669
17 7611 5184
18 7462 3590
19 7732 4723
20 5900 3561
21 4483 3369
22 6101 1110
23 5199 2182
24 1633 2809
25 4307 2322
26 675 1006
27 7555 4819
28 7541 3981
29 3177 756
30 7352 4506
31 7545 2801
32 3245 3305
33 6426 3173
34 4608 1198
35 23 2216
36 7248 3779
37 7762 4595
38 7392 2244
39 3484 2829
40 6271 2135
41 4985 140
42 1916 1569
43 7280 4899
44 7509 3239
45 10 2676
46 6807 2993
47 5185 3258
48 3023 1942
EOF

4.2 Java 完整代码

4.2.1 TSP_Instance 实例类

package com.wskh.classes.tsp;

import lombok.Data;
import lombok.ToString;

/**
 * @Author：WSKH
 * @ClassName：TSP_Instance
 * @Description：
 * @Time：2023/5/13/22:20
 * @Email：1187560563@qq.com
 * @Blog：wskh0929.blog.csdn.net
 */
@Data
@ToString
public class TSP_Instance {
    // 实例名
    String name;
    // 城市数量
    int n;
    // 每个城市的坐标
    double[][] locations;
}

4.2.2 TSP_Solution 结果类

package com.wskh.classes.tsp;

import lombok.AllArgsConstructor;
import lombok.Data;
import lombok.NoArgsConstructor;
import lombok.ToString;

import java.util.Arrays;

/**
 * @Author：WSKH
 * @ClassName：TSP_Solution
 * @Description：
 * @Time：2023/5/13/22:52
 * @Email：1187560563@qq.com
 * @Blog：wskh0929.blog.csdn.net
 */
@Data
@NoArgsConstructor
@AllArgsConstructor
public class TSP_Solution {
    // 路程长度
    double pathLen;
    // 路径
    int[] path;

    public TSP_Solution copy() {
        return new TSP_Solution(pathLen, path.clone());
    }

    @Override
    public String toString() {
        return "pathLen = " + pathLen + " , path = " + Arrays.toString(path);
    }
}

4.2.3 TSP_Util 工具类

package com.wskh.utils;

import com.wskh.classes.tsp.TSP_Instance;

import java.io.BufferedReader;
import java.io.FileReader;
import java.io.IOException;

/**
 * @Author：WSKH
 * @ClassName：TSP_Util
 * @Description：
 * @Time：2023/5/13/22:15
 * @Email：1187560563@qq.com
 * @Blog：wskh0929.blog.csdn.net
 */
public class TSP_Util {
    // 读取tsp数据
    public static TSP_Instance readTSP_Instance(String path) throws IOException {
        TSP_Instance tspInstance = new TSP_Instance();
        BufferedReader bufferedReader = new BufferedReader(new FileReader(path));
        String line = null;
        int row = 1;
        while ((line = bufferedReader.readLine()) != null) {
            if (line.contains("NAME")) {
                tspInstance.setName(line.split(" : ")[1]);
            } else if (line.contains("DIMENSION")) {
                tspInstance.setN(Integer.parseInt(line.split(" : ")[1]));
                tspInstance.setLocations(new double[tspInstance.getN()][2]);
            } else if (row >= 7 && row < 7 + tspInstance.getN()) {
                String[] split = line.split(" ");
                int index = Integer.parseInt(split[0]) - 1;
                int x = Integer.parseInt(split[1]);
                int y = Integer.parseInt(split[2]);
                tspInstance.getLocations()[index][0] = x;
                tspInstance.getLocations()[index][1] = y;
            }
            row++;
        }
        bufferedReader.close();
        return tspInstance;
    }

    // 计算两点之间的取整的伪欧式距离
    public static double calcDistance(double[] p1, double[] p2) {
        return Math.ceil(Math.sqrt((Math.pow(p1[0] - p2[0], 2) + Math.pow(p1[1] - p2[1], 2)) / 10d));
    }

    // 评价函数，传入一个路径和距离矩阵，返回该路径的长度
    public static double calcPathLen(int[] path, double[][] distances) {
        double pathLen = 0d;
        for (int i = 0; i < path.length - 1; i++) {
            pathLen += distances[path[i]][path[i + 1]];
        }
        // 还要算上从最后一个城市回到起始城市的距离
        pathLen += distances[path[path.length - 1]][path[0]];
        return pathLen;
    }

}

4.2.4 TSP_Solver_ALNS 算法类

package com.wskh.meta_heuristics.ALNS.tsp;

import com.wskh.classes.tsp.TSP_Instance;
import com.wskh.classes.tsp.TSP_Solution;
import com.wskh.utils.TSP_Util;
import lombok.Data;

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Random;

/**
 * @Author：WSKH
 * @ClassName：TSP_Solver_SA
 * @Description：
 * @Time：2023/5/13/22:21
 * @Email：1187560563@qq.com
 * @Blog：wskh0929.blog.csdn.net
 */
@Data
public class TSP_Solver_ALNS {

    // 随机数种子
    Long seed;
    // 0~1 控制权重对破坏和修复方法的性能变化的敏感程度的衰减参数
    double lambda = 0.6;
    // 分数(w1>w2>w3>w4>0)
    double w1, w2, w3, w4;
    // 迭代次数
    int epochs = 5000;
    // 温度
    double c = 100d;
    // 冷却降温系数：一般取 0.8 ~ 0.99
    double alphaCooling = 0.9;

    // 构造函数
    public TSP_Solver_ALNS(Long seed, double lambda, double w1, double w2, double w3, double w4, int epochs, double c) {
        this.seed = seed;
        this.lambda = lambda;
        this.w1 = w1;
        this.w2 = w2;
        this.w3 = w3;
        this.w4 = w4;
        this.epochs = epochs;
        this.c = c;
    }

    // 城市数量
    int n;
    // 城市坐标
    double[][] locations;
    // 距离矩阵
    double[][] distances;
    // 随机数生成对象
    Random random;
    // 当前解
    TSP_Solution curSolution;
    // 最优解
    TSP_Solution bestSolution;
    // 销毁算子和修复算子的分数数组
    double[] destroyScores;
    double[] repairScores;

    // 求解函数
    public TSP_Solution solve(TSP_Instance tspInstance) {
        long startTime = System.currentTimeMillis();
        // 初始化操作
        init(tspInstance);
        System.out.println("城市数量为: " + n);
        System.out.println("初始解为: " + bestSolution);
        // 自适应大邻域搜索过程
        for (int epoch = 0; epoch < epochs; epoch++) {
            // 轮盘赌选择销毁算子对当前解进行破坏
            int destroyIndex = roulette(destroyScores);
            PartX partX = null;
            switch (destroyIndex) {
                case 0:
                    partX = destroyOperator1(curSolution.getPath());
                    break;
                case 1:
                    partX = destroyOperator2(curSolution.getPath());
                    break;
                case 2:
                    partX = destroyOperator3(curSolution.getPath());
                    break;
                default:
                    break;
            }
            assert partX != null;
            // 轮盘赌选择修复算子对部分解进行修复
            int repairIndex = roulette(repairScores);
            int[] newX = null;
            switch (repairIndex) {
                case 0:
                    newX = repairOperator1(partX);
                    break;
                case 1:
                    newX = repairOperator2(partX);
                    break;
                case 2:
                    newX = repairOperator3(partX);
                    break;
                default:
                    break;
            }
            assert newX != null;
            // 评价新序列
            double newPathLen = TSP_Util.calcPathLen(newX, distances);
            // 更新解和分数
            if (newPathLen < curSolution.getPathLen()) {
                destroyScores[destroyIndex] = lambda * destroyScores[destroyIndex] + (1 - lambda) * w2;
                repairScores[repairIndex] = lambda * repairScores[repairIndex] + (1 - lambda) * w2;
                curSolution = new TSP_Solution(newPathLen, newX);
                // 更新全局最优解
                if (newPathLen < bestSolution.getPathLen()) {
                    destroyScores[destroyIndex] = lambda * destroyScores[destroyIndex] + (1 - lambda) * w1;
                    repairScores[repairIndex] = lambda * repairScores[repairIndex] + (1 - lambda) * w1;
                    bestSolution = new TSP_Solution(newPathLen, newX);
                }
            } else {
                // 接受准则(模拟退火 Metropolis 准则)
                if (random.nextDouble() <= Math.exp((curSolution.getPathLen() - newPathLen) / c)) {
                    destroyScores[destroyIndex] = lambda * destroyScores[destroyIndex] + (1 - lambda) * w3;
                    repairScores[repairIndex] = lambda * repairScores[repairIndex] + (1 - lambda) * w3;
                    curSolution = new TSP_Solution(newPathLen, newX);
                } else {
                    destroyScores[destroyIndex] = lambda * destroyScores[destroyIndex] + (1 - lambda) * w4;
                    repairScores[repairIndex] = lambda * repairScores[repairIndex] + (1 - lambda) * w4;
                }
            }
            c *= alphaCooling;
        }
        // 输出结果
        System.out.println("destroyScores: " + Arrays.toString(destroyScores));
        System.out.println("repairScores: " + Arrays.toString(repairScores));
        System.out.println("最终找到的最优解为: " + bestSolution);
        System.out.println("求解用时: " + (System.currentTimeMillis() - startTime) / 1000d + " s");
        return bestSolution;
    }

    // 轮盘赌：传入权重（分数）向量，根据权重随机一个索引并返回（flag：true，销毁；否则，修复）
    private int roulette(double[] scores) {
        double sum = 0;
        for (double s : scores) {
            sum += s;
        }
        double[] cumulativeProbabilityArr = new double[scores.length];
        for (int i = 0; i < cumulativeProbabilityArr.length; i++) {
            cumulativeProbabilityArr[i] = scores[i] / sum;
            if (i - 1 >= 0) {
                cumulativeProbabilityArr[i] += cumulativeProbabilityArr[i - 1];
            }
        }
        double r = random.nextDouble();
        for (int i = 0; i < cumulativeProbabilityArr.length; i++) {
            if (r <= cumulativeProbabilityArr[i]) {
                return i;
            }
        }
        return -1;
    }

    // 销毁算子1：随机删除k个点
    private PartX destroyOperator1(int[] X) {
        PartX partX = new PartX();
        int k = random.nextInt(X.length);
        boolean[] removed = new boolean[X.length];
        for (int i = k; i > 0; i--) {
            int r = random.nextInt(X.length);
            while (removed[r]) {
                r = random.nextInt(X.length);
            }
            removed[r] = true;
        }
        for (int i = 0; i < removed.length; i++) {
            if (removed[i]) {
                partX.removeIndexList.add(i);
            } else {
                partX.indexList.add(i);
            }
        }
        return partX;
    }

    // 销毁算子2：随机删除序列中的一个片段
    private PartX destroyOperator2(int[] X) {
        PartX partX = new PartX();
        int left = random.nextInt(X.length);
        int right = random.nextInt(X.length);
        // 确保 left <= right
        if (left > right) {
            right = left ^ right;
            left = left ^ right;
            right = left ^ right;
        }
        for (int i = 0; i < X.length; i++) {
            if (i >= left && i <= right) {
                partX.removeIndexList.add(i);
            } else {
                partX.indexList.add(i);
            }
        }
        return partX;
    }

    // 销毁算子3：破坏一对交叉的边
    private PartX destroyOperator3(int[] X) {
        PartX partX = new PartX();
        for (int left1 = 0; left1 < n; left1++) {
            int right1 = left1 + 1 >= n ? 0 : left1 + 1;
            for (int left2 = right1 + 1; left2 < n; left2++) {
                int right2 = left2 + 1 >= n ? 0 : left2 + 1;
                // 判断两个边(线段)是否相交
                if (isIntersect(locations[left1], locations[right1], locations[left2], locations[right2])) {
                    for (int i = 0; i < n; i++) {
                        if (i == left1 || i == left2 || i == right1 || i == right2) {
                            partX.removeIndexList.add(i);
                        } else {
                            partX.indexList.add(i);
                        }
                    }
                    return partX;
                }
            }
        }
        // 如果没有交叉的边，那就 destroyOperator1
        return destroyOperator1(X);
    }

    // 判断两个边(线段)是否相交
    private boolean isIntersect(double[] line1_p1, double[] line1_p2, double[] line2_p1, double[] line2_p2) {
        // 判断两个线段是否相交（共线，顶点相交的情况不算，如果要考虑，只需要把跨立实验的>=改为>即可）
        // 快速排斥实验
        if ((Math.max(line1_p1[0], line1_p2[0])) < (Math.min(line2_p1[0], line2_p2[0])) ||
                (Math.max(line1_p1[1], line1_p2[1])) < (Math.min(line2_p1[1], line2_p2[1])) ||
                (Math.max(line2_p1[0], line2_p2[0])) < (Math.min(line1_p1[0], line1_p2[0])) ||
                (Math.max(line2_p1[1], line2_p2[1])) < (Math.min(line1_p1[1], line1_p2[1]))) {
            return false;
        }
        // 跨立实验
        if ((((line1_p1[0] - line2_p1[0]) * (line2_p2[1] - line2_p1[1]) - (line1_p1[1] - line2_p1[1]) * (line2_p2[0] - line2_p1[0])) *
                ((line1_p2[0] - line2_p1[0]) * (line2_p2[1] - line2_p1[1]) - (line1_p2[1] - line2_p1[1]) * (line2_p2[0] - line2_p1[0]))) >= 0 ||
                (((line2_p1[0] - line1_p1[0]) * (line1_p2[1] - line1_p1[1]) - (line2_p1[1] - line1_p1[1]) * (line1_p2[0] - line1_p1[0])) *
                        ((line2_p2[0] - line1_p1[0]) * (line1_p2[1] - line1_p1[1]) - (line2_p2[1] - line1_p1[1]) * (line1_p2[0] - line1_p1[0]))) >= 0) {
            return false;
        }
        return true;
    }

    // 修复算子1：随机插入修复
    private int[] repairOperator1(PartX partX) {
        for (int removeIndex : partX.removeIndexList) {
            int randomInsertIndex = random.nextInt(partX.indexList.size() + 1);
            partX.indexList.add(randomInsertIndex, removeIndex);
        }
        int[] X = new int[n];
        int i = 0;
        for (int index : partX.indexList) {
            X[i++] = index;
        }
        return X;
    }

    // 修复算子2：启发式插入修复
    private int[] repairOperator2(PartX partX) {
        for (int removeIndex : partX.removeIndexList) {
            if (partX.indexList.isEmpty()) {
                partX.indexList.add(removeIndex);
                continue;
            }
            // 由于插入到第一个和最后一个是等效的，所以 insertIndex < partX.indexList.size() 即可
            int bestInsertIndex = -1;
            double bestObj = 0;
            for (int insertIndex = 0; insertIndex < partX.indexList.size(); insertIndex++) {
                int left = (insertIndex - 1 < 0 ? n - 1 : insertIndex - 1);
                int right = insertIndex;
                double obj = 0d;
                obj += TSP_Util.calcDistance(locations[left], locations[removeIndex]);
                obj += TSP_Util.calcDistance(locations[removeIndex], locations[right]);
                if (bestInsertIndex < 0 || bestObj > obj) {
                    bestInsertIndex = insertIndex;
                    bestObj = obj;
                }
            }
            partX.indexList.add(bestInsertIndex, removeIndex);
        }
        int[] X = new int[n];
        int i = 0;
        for (int index : partX.indexList) {
            X[i++] = index;
        }
        return X;
    }

    // 修复算子3：直接接到后面
    private int[] repairOperator3(PartX partX) {
        int[] X = new int[n];
        int i = 0;
        for (int index : partX.indexList) {
            X[i++] = index;
        }
        for (int index : partX.removeIndexList) {
            X[i++] = index;
        }
        return X;
    }

    // 初始化操作
    private void init(TSP_Instance tspInstance) {
        n = tspInstance.getN();
        destroyScores = new double[3];
        repairScores = new double[3];
        Arrays.fill(destroyScores, 1);
        Arrays.fill(repairScores, 1);
        locations = tspInstance.getLocations();
        random = seed == null ? new Random() : new Random(seed);
        // 计算距离矩阵
        distances = new double[n][n];
        for (int i = 0; i < distances.length; i++) {
            for (int j = i + 1; j < distances.length; j++) {
                // i到j等于j到i
                distances[i][j] = TSP_Util.calcDistance(locations[i], locations[j]);
                distances[j][i] = distances[i][j];
            }
        }
        // 生成初始解，为简单起见，我们考虑使用字典顺序的生成初始解决方案
        curSolution = new TSP_Solution();
        curSolution.setPath(new int[n]);
        for (int i = 0; i < n; i++) {
            curSolution.getPath()[i] = i;
        }
        curSolution.setPathLen(TSP_Util.calcPathLen(curSolution.getPath(), distances));
        bestSolution = curSolution.copy();
    }

    // 部分序列对象
    static class PartX {
        LinkedList<Integer> indexList = new LinkedList<>();
        LinkedList<Integer> removeIndexList = new LinkedList<>();
    }
}

4.2.5 RunAndPlot 运行类

package com.wskh.meta_heuristics.ALNS.tsp;

import com.wskh.classes.tsp.TSP_Instance;
import com.wskh.classes.tsp.TSP_Solution;
import com.wskh.utils.TSP_Util;
import javafx.animation.KeyFrame;
import javafx.animation.Timeline;
import javafx.event.ActionEvent;
import javafx.event.EventHandler;
import javafx.scene.Scene;
import javafx.scene.canvas.Canvas;
import javafx.scene.canvas.GraphicsContext;
import javafx.scene.control.Button;
import javafx.scene.layout.AnchorPane;
import javafx.scene.paint.Color;
import javafx.scene.shape.Circle;
import javafx.scene.shape.LineTo;
import javafx.scene.shape.MoveTo;
import javafx.scene.shape.Path;
import javafx.stage.Stage;
import javafx.util.Duration;

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;

/**
 * @Author：WSKH
 * @ClassName：Run
 * @Description：
 * @Time：2023/5/14/11:52
 * @Email：1187560563@qq.com
 * @Blog：wskh0929.blog.csdn.net
 */
public class RunAndPlot extends javafx.application.Application {

    // 可视化区域的宽度
    int stageW = 1000;
    // 可视化区域的高度
    int stageH = 1000;
    // 坐标偏移
    int offsetX = 100;
    int offsetY = 100;

    // 主要函数
    @Override
    public void start(Stage primaryStage) throws Exception {

        // 初始化画布和面板
        AnchorPane pane = new AnchorPane();
        Canvas canvas = initCanvas(stageW - offsetX * 2, stageH - offsetY * 2);
        canvas.relocate(offsetX, offsetY);
        pane.getChildren().add(canvas);

        // 读取tsp数据
        TSP_Instance tspInstance = TSP_Util.readTSP_Instance("data/tsp/att48.tsp");
        // 固定使用随机数种子
        Long seed = 2023L;
        System.out.println("------------------------- 自适应大邻域搜索算法求解TSP问题 -----------------------------");
        TSP_Solution solution = new TSP_Solver_ALNS(seed, 0.6,1.5, 1.2, 0.8, 0.1, 100000, 300).solve(tspInstance);

        // 获取最佳路径
        int[] bestPath = solution.getPath().clone();

        // 按照屏幕尺寸等比例调整城市坐标
        List<double[]> fitLocationList = fitLocation(tspInstance.getLocations());

        // 绘制城市
        HashMap<Integer, Circle> map = new HashMap<>();
        List<Circle> circleList = new ArrayList<>();
        for (double[] position : fitLocationList) {
            Circle circle = new Circle(position[0], position[1], 5);
            pane.getChildren().add(circle);
            circleList.add(circle);
        }

        // 添加播放按钮
        Button button = new Button("播放");
        final int[] pCnt = {0};
        button.setOnAction(new EventHandler<ActionEvent>() {
            // 按钮点击事件
            @Override
            public void handle(ActionEvent event) {
                // 路径 动画
                Timeline animation = new Timeline(new KeyFrame(Duration.millis(50), new EventHandler<ActionEvent>() {
                    @Override
                    public void handle(ActionEvent event) {
                        if (pCnt[0] < bestPath.length - 1) {
                            int cur = bestPath[pCnt[0]];
                            int next = bestPath[pCnt[0] + 1];
                            double[] p1 = fitLocationList.get(cur);
                            double[] p2 = fitLocationList.get(next);
                            Path path = new Path();
                            path.getElements().add(new MoveTo(p1[0], p1[1]));
                            path.getElements().add(new LineTo(p2[0], p2[1]));
                            pane.getChildren().add(path);
                            pCnt[0]++;
                        } else if (pCnt[0] == bestPath.length - 1) {
                            int cur = bestPath[pCnt[0]];
                            int next = bestPath[0];
                            double[] p1 = fitLocationList.get(cur);
                            double[] p2 = fitLocationList.get(next);
                            Path path = new Path();
                            path.getElements().add(new MoveTo(p1[0], p1[1]));
                            path.getElements().add(new LineTo(p2[0], p2[1]));
                            pane.getChildren().add(path);
                            pCnt[0]++;
                        }
                    }
                }));
                animation.setCycleCount(Timeline.INDEFINITE);
                animation.play();
            }
        });
        pane.getChildren().add(button);

        // 一切就绪，准备展示
        primaryStage.setTitle("TSP路径可视化");
        primaryStage.setScene(new Scene(pane, stageW, stageH));
        primaryStage.show();
    }

    private List<double[]> fitLocation(double[][] locations) {
        List<double[]> locationList = new ArrayList<>();
        for (double[] location : locations) {
            locationList.add(location.clone());
        }
        // 获取宽度和高度方向上的最大值
        double maxX = locationList.get(0)[0];
        double maxY = locationList.get(0)[1];
        for (double[] position : locationList) {
            maxX = Math.max(maxX, position[0]);
            maxY = Math.max(maxY, position[1]);
        }
        // 计算缩放比例
        double rateX = (stageW - 2 * offsetX) / maxX;
        double rateY = (stageH - 2 * offsetY) / maxY;
        // 按照比例自适应调整
        List<double[]> fitLocationList = new ArrayList<>();
        for (double[] position : locationList) {
            fitLocationList.add(new double[]{position[0] * rateX + offsetX, position[1] * rateY + offsetY});
        }
        return fitLocationList;
    }

    // 初始化画布对象
    private Canvas initCanvas(double l, double w) {
        Canvas canvas = new Canvas(l, w);
        GraphicsContext gc = canvas.getGraphicsContext2D();
        // 边框
        gc.setStroke(Color.BLACK);
        gc.setLineWidth(2);
        gc.strokeRect(0, 0, l, w);
        // 填充
        gc.setFill(new Color(127 / 255d, 255 / 255d, 170 / 255d, 1d));
        gc.fillRect(0, 0, l, w);
        return canvas;
    }

    public static void main(String[] args) {
        launch(args);
    }
}

4.3 运行结果展示

控制台输出：

------------------------- 自适应大邻域搜索算法求解TSP问题 -----------------------------
城市数量为: 48
初始解为: pathLen = 49840.0 , path = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47]
destroyScores: [0.10000000000000003, 0.10000000000000003, 0.10000000000000003]
repairScores: [0.10000000000000003, 0.10000000000000003, 0.10000000000000003]
最终找到的最优解为: pathLen = 31444.0 , path = [0, 2, 28, 1, 44, 34, 3, 25, 9, 4, 17, 5, 39, 6, 32, 8, 33, 7, 10, 14, 24, 22, 11, 12, 47, 13, 15, 21, 18, 16, 36, 31, 20, 19, 26, 29, 23, 27, 30, 37, 35, 38, 40, 41, 42, 43, 45, 46]
求解用时: 0.383 s