参考文章链接:https://blog.csdn.net/qq_30460949/article/details/121990114
仅自学做笔记用,后续有错误会更改
理论
1.Smooth/blur是图像处理中最简单和常用的操作之一
2.使用该操作的原因之一就是为了给图像预处理的时候减低噪声
3.使用Smooth/Blur操作其背后是数学的卷积计算
4.通常卷积算子计算都是线性操作,所以又叫线性滤波
均值滤波
均值滤波其原理图如下

高斯滤波
高斯滤波,这是一个建立在高斯正态分布基础上的滤波器。
一维高斯函数:
可以看到,G(x)的跟sigma的取值有极大的关系。
sigma取值越大,图像越平缓
sigma取值越小,图像越尖锐

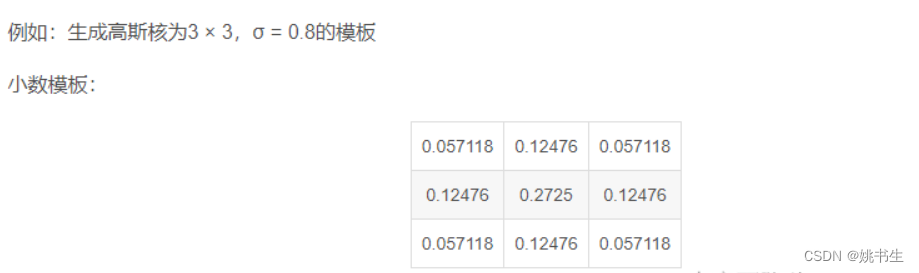

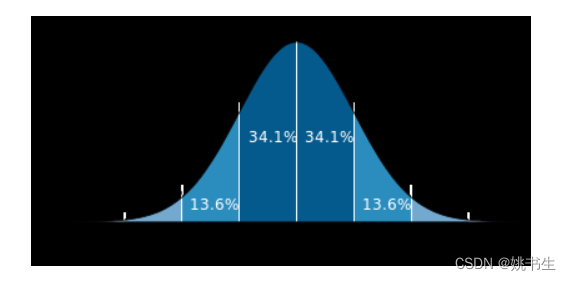
从以上描述中我们可以看出,高斯滤波模板中最重要的参数就是高斯分布的标准差σ。它代表着数据的离散程度,如果σ较小,那么生成的模板中心系数越大,而周围的系数越小,这样对图像的平滑效果就不是很明显;相反,σ较大时,则生成的模板的各个系数相差就不是很大,比较类似于均值模板,对图像的平滑效果就比较明显。通过下面的一维高斯分布图也可验证上述观点。
二维高斯函数: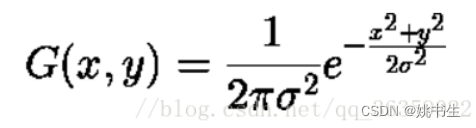
G(x,y)在x轴y轴上的分布是一个突起的帽子的形状。这里的sigma可以看作两个值,一个是x轴上的分量sigmaX,另一个是y轴上的分量sigmaY。对图像处理可以直接使用sigma并对图像的行列操作,也可以用sigmaX对图像的行操作,再用sigmaY对图像的列操作。它们是等价的:
当sigmaX和sigmaY取值越大,整个形状趋近于扁平
当sigmaX和sigmaY取值越小,整个形状越突起

高斯滤波原理就是将上图的二维正态分布应用在二维的矩阵上,G(x,y)的值就是矩阵上的权值,将得到的权值进行归一化,将权值的范围约束在[0,1]之间,并且所有的值的总和为1。
假设一个33的核,sigma取值1.5以及sigma取5.0,归一化后其权值分布分别是:

假设一个55的核,sigma取值1.5以及sigma取5.0,经归一化后其权值分布分别是:
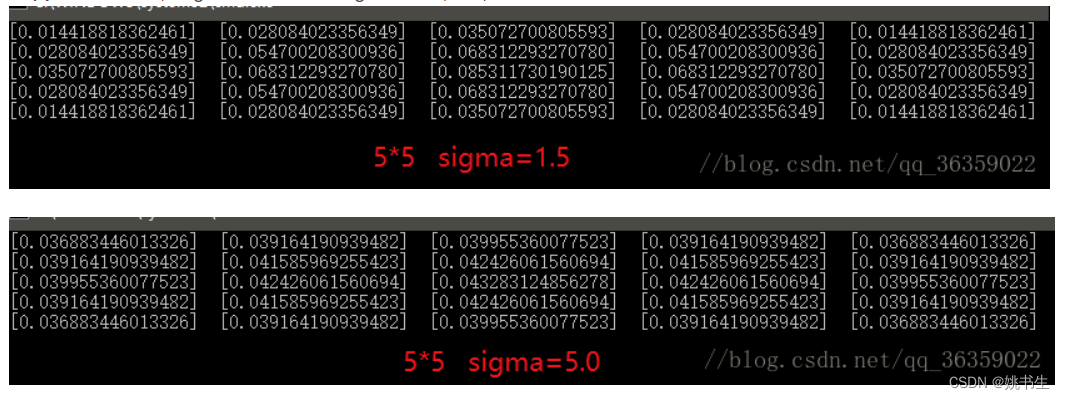
可以看到,权值的分布是以中间高四周低来分布的。并且距离中心越远,其对中心点的影响就越小,权值也就越小。
总结:
核大小固定,sigma值越大,权值分布越平缓。因此邻域各点值对输出值的影响越大,最终结果造成图像越模糊
核大小固定,sigma值越小,权值分布越突起。因此邻域各点值对输出值的影响越小,图像变化越小。假如中心点权值为1,其他点权值为0,最终结果是图像没有任何变化。
sigma固定时,核越大图像越模糊
sigma固定时,核越小图像变化越小
相关API
均值模糊:
blur(Mat src, Mat dst, Size(xredius,yradius), Point(-1,-1));
高斯模糊:
GaussianBlur(Mat src,Mat dst,Size(11,11), sigmax,sigmay);其中Size(x,y)的x和y必须是正数而且是奇数
代码示例
Mat srcImageMat,dstImageMat;
srcImageMat = imread(...);
// 均值滤波 3*3的格子(也就是核), 后边Point(-1,-1)表示操作的其中心点
// blur(srcImageMat, dstImageMat, Size(3,3), Point(-1,-1));
// 均值滤波 1*15的格子, 也就是仅对Y轴进行模糊
// blur(srcImageMat, dstImageMat, Size(1,15), Point(-1,-1));
// 均值滤波 15*1的格子, 也就是仅对X轴进行模糊(也就是电影镜头横向移动时出现的模糊)
// blur(srcImageMat, dstImageMat, Size(15,1), Point(-1,-1));
// 高斯滤波 核固定时,后边两个sigma值越大越模糊, 后边sigma值固定时, 核越大也越模糊
GaussianBlur(srcImageMat, dstImageMat,Size(5,5), 11, 11);