在农业领域中,将机器学习和深度学习模型结合应用有着广泛的实用意义,在这块相关的实践中以往的项目开发实践则是主要集中在农作物种植相关的,今天本文的主要目的就是开发构建果树叶部疾病识别分析系统,这里是以苹果果树叶部疾病数据集为例的,首先看下效果图:
接下来看下数据集,一共包含5个类别的数据集,如下:
【AlternariaBoltch】

【BrownSpot】

【GreySpot】

【Mosaic】

【Rust】

这里轻量级的CNN模型采用的是3层卷积神经网络,模型详情参数结构图如下所示:

默认200次epoch迭代计算,日志输出如下所示:


整个训练过程中准确率曲线和损失值曲线如下所示:

结果详情如下所示:
Epoch 00194: val_loss did not improve from 0.02363
Epoch 195/200
26377/26377 [==============================] - 6s 237us/step - loss: 0.0310 - acc: 0.9814 - val_loss: 0.0270 - val_acc: 0.9833
Epoch 00195: val_loss did not improve from 0.02363
Epoch 196/200
26377/26377 [==============================] - 6s 237us/step - loss: 0.0303 - acc: 0.9799 - val_loss: 0.0249 - val_acc: 0.9799
Epoch 00196: val_loss did not improve from 0.02363
Epoch 197/200
26377/26377 [==============================] - 6s 237us/step - loss: 0.0291 - acc: 0.9804 - val_loss: 0.0243 - val_acc: 0.9841
Epoch 00197: val_loss did not improve from 0.02363
Epoch 198/200
26377/26377 [==============================] - 6s 237us/step - loss: 0.0283 - acc: 0.9821 - val_loss: 0.0246 - val_acc: 0.9837
Epoch 00198: val_loss did not improve from 0.02363
Epoch 199/200
26377/26377 [==============================] - 6s 235us/step - loss: 0.0286 - acc: 0.9802 - val_loss: 0.0238 - val_acc: 0.9837
Epoch 00199: val_loss did not improve from 0.02363
Epoch 200/200
26377/26377 [==============================] - 6s 235us/step - loss: 0.0289 - acc: 0.9807 - val_loss: 0.0243 - val_acc: 0.9833
Epoch 00200: val_loss did not improve from 0.02363
dict_keys(['val_loss', 'val_acc', 'loss', 'acc'])
Accuracy: 98.33%
=====================Finish=========================
可以看到:模型的识别效果还是很不错的,达到了98%以上。
到这里本身就结束了,但是突然想尝试基于机器学习方法也开发这样的疾病识别模型,作为和深度学习模型的对比。首先看下整体效果:

这里机器学习模型采用的路线是HOG+SVM这一经典的组合。
HOG(Histogram of Oriented Gradients)是一种用于图像特征提取的算法,广泛应用于计算机视觉领域,特别是目标检测任务。HOG算法通过计算图像局部区域的梯度方向直方图来描述图像的纹理和形状特征。以下是HOG算法的基本原理:
-
图像梯度计算:首先,将输入图像转换为灰度图像,然后计算每个像素的梯度信息。通常使用Sobel算子计算图像的水平和垂直梯度。
-
图像划分为小块:将图像划分为小的重叠区域(cell)。每个小区域通常为正方形,并包含一组像素。每个小区域的大小和形状可以根据具体需求进行选择。
-
梯度方向直方图计算:对于每个小区域,计算其内像素的梯度方向直方图。直方图将梯度方向范围划分为多个离散的方向区间,统计每个方向区间内梯度的强度值。
-
块归一化:将相邻的几个小区域(通常为2x2个)组合成一个块(block)。对每个块内的梯度方向直方图进行归一化,以增加算法对光照变化的鲁棒性。
-
特征向量生成:将所有块的归一化直方图串联起来,生成最终的特征向量。这个特征向量包含了图像的纹理和形状特征,并可以用于后续的目标检测或分类任务。
-
目标检测:使用生成的特征向量进行目标检测。通常使用滑动窗口的方法在图像上进行扫描,提取局部区域的特征向量,并使用分类器(如支持向量机)判断该区域是否包含目标。
HOG算法通过对图像局部区域的梯度方向进行统计和描述,捕捉了图像的纹理和形状信息,从而具备一定的不变性和鲁棒性。它在人体检测、行人检测等任务中取得了很好的效果,并成为了计算机视觉领域的重要算法之一。
SVM(Support Vector Machine)是一种用于分类和回归分析的机器学习算法。它基于统计学习理论中的结构风险最小化原则,通过找到一个最优超平面来划分不同类别的样本。以下是SVM算法的基本原理:
-
数据表示:假设我们有一个训练数据集,其中包含带有标签的样本。每个样本由一个特征向量和对应的类别标签组成。
-
构建超平面:SVM的目标是找到一个超平面,将不同类别的样本完全分开。超平面是一个(N-1)维的决策边界,其中N是样本的特征维度。对于二分类问题,超平面将数据空间划分为两个不同的区域,使得同一类别的样本在同一边,不同类别的样本在不同边。
-
最大化间隔:SVM选择具有最大间隔(Margin)的超平面。间隔是指超平面到最近的样本点的距离,SVM试图找到使得间隔最大化的超平面。最大间隔有助于提高分类器的鲁棒性,使其对新样本的泛化能力更强。
-
支持向量:在构建超平面的过程中,只有一部分样本被用来确定超平面,这些样本被称为支持向量(Support Vectors)。支持向量是离超平面最近的样本点,它们对于确定超平面的位置和形状起着关键作用。
-
核函数:对于非线性可分的问题,SVM可以通过使用核函数来将数据映射到高维空间中进行处理。核函数可以将低维空间中的样本映射到高维空间,使得在高维空间中可以更容易地找到一个线性可分的超平面。
-
分类和回归:一旦超平面确定,SVM可以用于分类新的未标记样本。通过计算新样本点到超平面的位置关系,可以确定其所属的类别。SVM也可以扩展到回归问题中,通过拟合一个带有最小误差的超平面来预测连续型目标变量。
SVM具有在高维空间中进行分类和回归的能力,并且对于少量支持向量的改变具有鲁棒性。它在许多实际应用中表现良好,如文本分类、图像识别、生物信息学等领域。
特征向量化核心代码实现如下所示:
def dataset2Feature(dataDir="dataset/", save_path="hogFeature.json"):
"""
特征向量化
"""
feature = []
for one_person in os.listdir(dataDir):
oneDir = dataDir + one_person + "/"
for one_pic in os.listdir(oneDir):
one_path = oneDir + one_pic
print("one_path: ", one_path)
one_vec = singleImg2Vector(pic=one_path)
one_label = one_person
one_vec.append(one_label)
print("one_vec_length: ", len(one_vec))
feature.append(one_vec)
with open(save_path, "w") as f:
f.write(json.dumps(feature))模型建模核心代码实现如下所示:
#训练拟合
if not os.path.exists(model_path):
model.fit(X_train, y_train)
else:
model = loadModel(model_path)
#预测
y_predict = model.predict(X_test)
y_pred = y_predict.tolist()
#计算准确率
accuracy = model.score(X_test, y_test)
print("SVM model accuracy: ", accuracy)
Precision,Recall,F1=calThree(y_test,y_pred)
saveModel(model,save_path=model_path)
result={}
result['accuracy'],result['F_value']=accuracy,F1
result['precision'],result['recall']=Precision,Recall
print('type: ', type(y_test), type(y_pred))
result['y_true'],result['y_pred']=y_test,y_pred
plotConfusionMatrix(y_test, y_pred, save_path = saveDir + 'ConfusionMatrix.png')接下来我们看下结果详情:
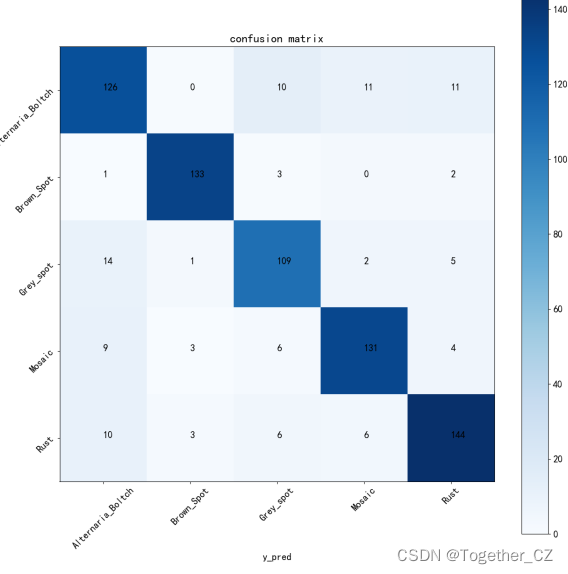
准确率相关评估指标如下所示:
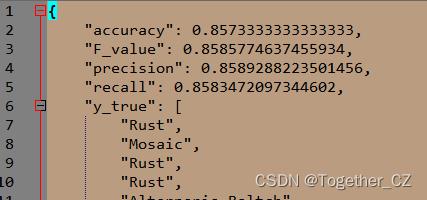
可以看到:机器学习达到了85%以上的准确率,虽说也是不错的效果了,但是和深度学习CNN模型相比来说还是逊色不少的。