divmod

-- divmod.adb
package body DivMod with SPARK_Mode is

   procedure DivMod(X : Positive; N : Positive; K : out Natural; Remainder : out Natural)
   is
      Y : Natural := X;
   begin
      K := 0;
      while Y >= N loop
         Y := Y - N;
         K := K + 1;
      end loop;
      Remainder := Y;
   end DivMod;


end DivMod;

--divmod.ads

package DivMod with SPARK_Mode is

   procedure DivMod(X : in Positive; N : in Positive; K : out Natural;
                    Remainder : out Natural);

end DivMod;

--main.adb

with Ada.Integer_Text_IO;
use Ada.Integer_Text_IO;
with Ada.Text_IO;
use Ada.Text_IO;
with DivMod;


procedure Main with SPARK_Mode is
   K : Natural;
   R : Natural;
   X : Integer;
   N : Integer;
begin
   Put_Line("Compute the result and remainder of X/N, via repeated subtraction.");
   Put_Line("The result and remainder are numbers K and R where X = K * N + R and R < N");
   Put("Enter a positive integer for X: ");
   Get(X);
   Put("Enter a positive integer for N: ");
   Get(N);
   if (X > 0 and N > 0) then
      DivMod.DivMod(X,N,K,R);
      Put("K: "); Put(K); New_Line;
      Put("R: "); Put(R); New_Line;

      -- assert that the result is correct
      pragma Assert (X = K * N + R and R < N);

      -- SPARK needs some help to conclude that X/N = K.
      -- We derive that final result step-by-step

      -- firstly K is not greater than X/N
      pragma Assert (K * N <= X);
      pragma Assert (X/N >= K);

      -- secondly K is not lower than X/N
      pragma Assert (if K < Integer'Last and then Integer'Last / N > K + 1 then
                        N * (K + 1) > X);
      pragma Assert (X/N <= K);

      -- therefore K is exactly equal to X/N
      pragma Assert (X/N = K);
   else
      Put_Line("X and N must both be positive. Exiting.");
   end if;
end Main;

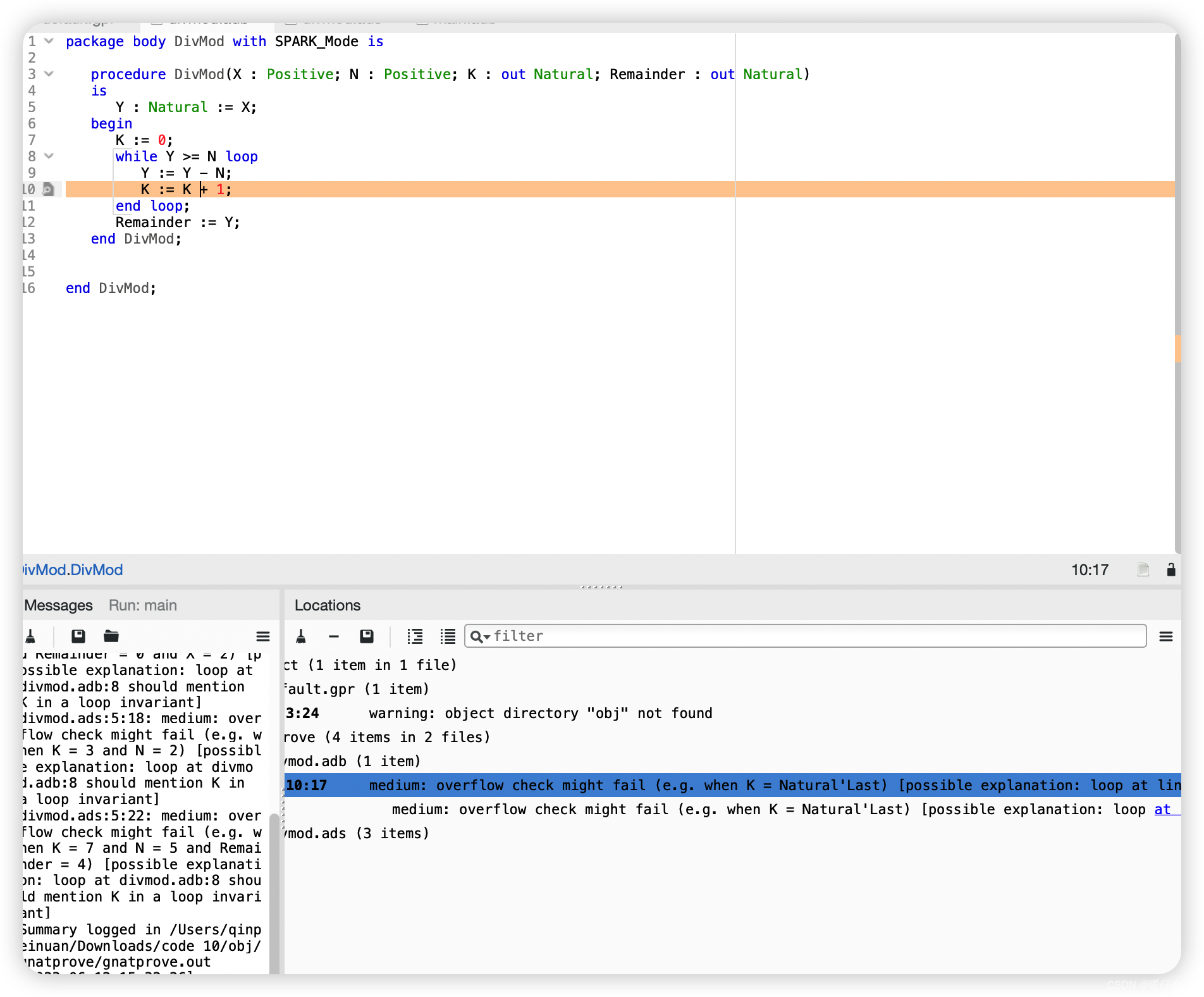
问题：Now run the SPARK prover: SPARK → Prove All. You will see that the provided main.adb contains a number of pragma Assert statements. These are assertions that the SPARK prover tries to prove always hold.
You will see that the assertion X = K * N + R and R < N in main.adb cannot be proved. (You
may also see potential problems reported in the DivMod package, but we will come to those later.)
This is because the DivMod procedure has no contract (pre/postcondition annotations), so the SPARK prover cannot tell anything about K and R after it is called.

问题：Add a postcondition annotation to the DivMod procedure in divmod.ads to allow the failing assert to be proved. Hint: this postcondition should state what is true about K and R in terms of X and N, after DivMod returns.

• 上述问题的原因就是：我们在 main.adb 中使用了 assert，但是由于在 divmod.ads 中我们没有使用 post 来向程序发布 X = K * N + Remainder 这个关系，所以在 main.adb 中经过 assert 的时候就没法满足，因此我们只需要在 divmod.adb 中加入这个 post condition 即可

package DivMod with SPARK_Mode is
   procedure DivMod(X : in Positive; N : in Positive; K : out Natural;
                    Remainder : out Natural) with
   Post=> (X = K * N + Remainder);
end DivMod;

• 上述问题解决

• 你可以将 post condition 的作用看成：向程序显示地声明某个 procedure 或者 function 的执行结果，以便 SPARK 进行检查

问题： Now run the SPARK Prover again. Now the assertions in main.adb should be able to be proved, using the contract on DivMod. However, the SPARK prover cannot actually prove that the contract holds.
It also cannot prove that the loop in DivMod won’t cause integer overflow.

To help it prove these, we need to add a suitable loop invariant annotation for the while-loop in DivMod. To work out what the invariant should say, you can add print statements to this loop to get it to print out the values of Y and K each time through the loop. Then look for a relationship that always holds between Y, K, N and X.
Once you have figured out the invariant, add an appropriate annotation to the while-loop: pragma Loop Invariant (. . . your invariant goes here . . .);

package body DivMod with SPARK_Mode is
   procedure DivMod(X : Positive; N : Positive; K : out Natural; Remainder : out Natural)
   is
      Y : Natural := X;
   begin
      K := 0;
      while Y >= N loop
         Y := Y - N;
         K := K + 1;
         pragma Loop_Invariant (Y <= X);
         pragma Loop_Invariant (Y + N * K = X);
      end loop;
      Remainder := Y;
   end DivMod;
end DivMod;

循环不变量 v.s. 后置条件

循环不变量和后置条件（postcondition）都是用于验证程序正确性的关键工具，但它们在具体用途上有一些区别。

• 循环不变量： 这是一个在循环的每一次迭代开始和结束时都保持为真的条件。循环不变量是在循环的过程中不断保持的一个条件或属性，它可以帮助我们理解循环的行为，保证循环的正确性。循环不变量通常会设计为捕获关于正在进行的计算的一些关键信息。
• 后置条件（postcondition）： 这是一个过程或函数结束时必须满足的条件。它描述了程序在执行后的预期状态。后置条件通常与前置条件（precondition，即程序开始前的状态）以及程序的实际操作一起使用，以证明程序的正确性。

在某种程度上，你可以认为循环不变量在循环的上下文中类似于后置条件， 因为它描述了每次循环迭代结束时的预期状态。但是，它们在语义上是不同的：后置条件描述的是程序结束时的状态，而循环不变量描述的是循环的每次迭代。

在形式化方法和程序验证中，通常会同时使用循环不变量和前置/后置条件，以帮助保证程序的正确性。

Now re-run the SPARK prover. If your invariant is correct, you should find that the SPARK prover does not report any problems. You have proved the correctness of your first program. Congratulations!

扩展思考

问题： If you have time: Look at the assert statements in main.adb more closely. The final one asserts that X / N = K, i.e. that K does in fact hold the result of performing integer division on X by N.
Try commenting out each of the assert statements above and re-running the SPARK prover for each. You should find that when one of these assertions is commented out, one of the following assertions cannot be proved.
This means that, to prove that following assertion, the SPARK prover first needs to know that the preceding one holds, i.e. it cannot derive the following assertion in one go but it needs some help: we first have to tell it to derive the intermediate assertion and, only then, can it derive the subsequent one. This can sometimes happen with automated provers like the SPARK prover. Using intermediate assertions like this can be a useful way, therefore, helping to derive extra facts that cannot be inferred automatically.