ECC
- 一、ECC简介
- 优缺点
- 运用
- 二、算法理论基础
- 1. 椭圆曲线的加法
- 2. 椭圆曲线的二倍运算
- 3. 同余运算
- 4. 有限域
- 5. 乘法逆元
- 三、算法公式
- 1、有限域的负元
- 2、有限域的加法, P + Q P + Q P+Q
- 3. 斜率计算(P=Q即要计算P点切线,需要求导)
- 4. 椭圆曲线加解密算法原理
- 5. 椭圆曲线签名算法原理
- 6. 签名过程
- 7. 验证过程
一、ECC简介
ECC全称为“Ellipse Curve Ctyptography”,是一种基于椭圆曲线数学的公开密钥加密算法。与传统的基于大质数分解难题的加密算法不同,该加密方式基于 “离散对数” 这种数学难题。
椭圆曲线在密码学中的使用是在1985年由Neal Koblitz和Victor Miller分别独立提出的。
优缺点
优点:
性能提升,同样的密钥长度,基于ECC加密要比基于RSA安全很多。而且计算量较小,处理速度更快,存储空间和传输带宽占用较少。
缺点:
-
曲线的选择很复杂。
ECC是基于椭圆曲线的离散对数问题,这并不是一个很好理解的问题,这里的椭圆曲线实际上并不是一个真正意义的椭圆,它的运算和椭圆类似,实际上是一个随着参数变化而不断变化的曲线,不同参数的选取会出现不同的曲线,不同的曲线就会形成不用的ECC标准,不同标准的ECC产生的加解密效果也是千差万别的。 -
有可能这条复杂的曲线被人植入了后门,别人就可以通过这个后门轻松的破解。
现行的一套很流行的ECC标准是由美国郭建安全局NAS发布的,这个标准就被很多人质疑是有被植入了后门的。 -
专利问题。
关于ECC的使用,很多人申请了很多的专利,现在关于ECC使用的专利大多数都掌握在一家公司的手中,这家公司就是黑莓。所以,当你想要构建自己的一套ECC标准的时候,可能不知道哪里就触及了它们的专利,卷入专利之争。
运用
目前我国居民二代身份证正在使用 256 位的椭圆曲线密码,虚拟货币比特币也选择ECC作为加密算法。
二、算法理论基础
椭圆曲线算法可以看作是定义在特殊集合下数的运算,满足一定的规则。椭圆曲线因为用二元三次方程y^2= x^3+ ax + b来表示,类似椭圆周长计算方程而得名。
1. 椭圆曲线的加法
过曲线上的两点A、B画一条直线,找到直线与椭圆曲线的交点,交点关于X轴对称位置的点,定义为A+B,即为加法。如下图A+B=C
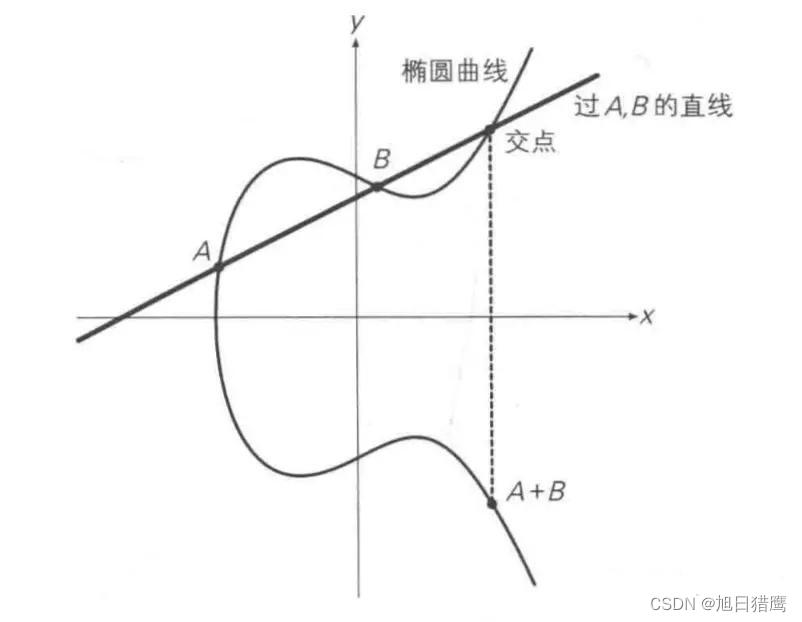
2. 椭圆曲线的二倍运算
上述方法无法解释A+A,即两点重合的情况,因此在这种情况下,将椭圆曲线在A点的切线,与椭圆曲线的交点,交点关于X轴对称的位置的点,定义为A+A,即2A,即为二倍运算。
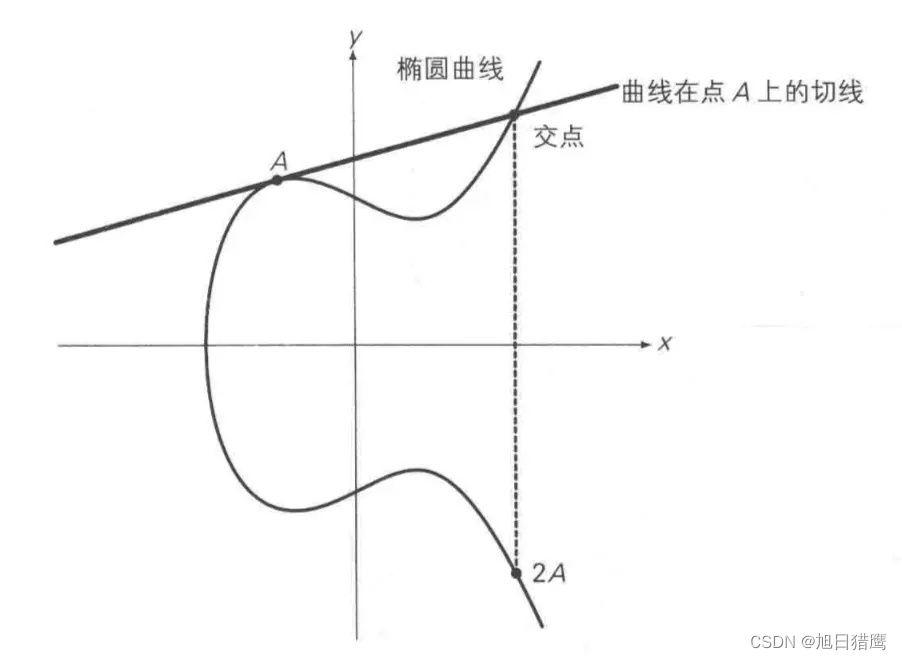
3. 同余运算
同余就是有相同的余数,两个整数 a、 b,若它们除以正整数 m所得的余数相等,则称 a, b对于模m同余。
a ≡ b ( m o d m ) a \equiv b(mod \quad m) a≡b(modm)
4. 有限域
椭圆曲线是连续的,并不适合用于加密;所以必须把椭圆曲线变成离散的点,要把椭圆曲线定义在有限域上。而椭圆曲线密码所使用的椭圆曲线是定义在有限域内,有限域最常见的例子是有限域GF§,指给定某质数p,由0,1,2…p-1共p个元素组成的整数集合中加法、二倍运算。例如GF(233)就是
y
2
=
(
x
3
+
7
)
(
m
o
d
223
)
y^2 = (x^3 + 7)(mod \quad 223)
y2=(x3+7)(mod223)
5. 乘法逆元
在模7乘法中:
- 1的逆元为 1 ( 1 ∗ 1 ) 1(1*1)%7 = 1 1(1∗1)
- 2的逆元为 4 ( 2 ∗ 4 ) 4(2*4)%7 = 1 4(2∗4)
- 3的逆元为 5 ( 3 ∗ 5 ) 5(3*5)%7 = 1 5(3∗5)
- 4的逆元为 2 ( 4 ∗ 2 ) 2(4*2)%7 = 1 2(4∗2)
- 5的逆元为 3 ( 5 ∗ 3 ) 3(5*3)%7 = 1 3(5∗3)
- 6的逆元为 6 ( 6 ∗ 6 ) 6(6*6)%7 = 1 6(6∗6)
三、算法公式
并不是所有的椭圆曲线都适合加密, y 2 = x 3 + a x + b y^2 = x^3 + ax + b y2=x3+ax+b 类可以用来加密的椭圆曲线,也是最为简单的一类。
针对曲线Ep(a,b)表示为 y 2 = x 3 + a x + b ( m o d p ) , x , y ∈ [ 0 , p ] , p 为质数 y^2 = x^3 + ax + b(mod \quad p), x,y \in [0,p], p为质数 y2=x3+ax+b(modp),x,y∈[0,p],p为质数
该曲线关于x轴对称。选择两个满足下列条件的小于p(p为素数)的非负整数a、b,要求满足以下条件
3
a
3
+
27
b
2
≠
0
3a^3 + 27b^2 \neq 0
3a3+27b2=0
1、有限域的负元
P ( x , y ) P(x,y) P(x,y) 的负元是 ( x , − y m o d p ) = ( x , p − y ) (x, -y \quad mod \quad p) = (x, p - y) (x,−ymodp)=(x,p−y)
2、有限域的加法, P + Q P + Q P+Q
P
(
x
1
,
y
1
)
P(x_1, y_1)
P(x1,y1),
Q
(
x
2
,
y
2
)
Q(x_2, y_2)
Q(x2,y2)和
R
(
x
3
,
y
3
)
R(x_3, y_3)
R(x3,y3)三点(其中R是PQ直线与曲线的交点的关于x轴的对称点,即
R
=
P
+
Q
R = P + Q
R=P+Q)有如下关系:
x
3
≡
k
2
−
x
1
−
x
2
(
m
o
d
p
)
x_3 \equiv k^2 - x_1 - x_2(mod \quad p)
x3≡k2−x1−x2(modp)
x
3
≡
k
2
−
x
1
−
x
2
(
m
o
d
p
)
x_3 \equiv k^2 - x_1 - x_2(mod \quad p)
x3≡k2−x1−x2(modp)
3. 斜率计算(P=Q即要计算P点切线,需要求导)
若
P
=
Q
P = Q
P=Q,则
k
=
(
2
x
2
+
a
)
/
2
y
1
k = (2x_2 + a)/2y_1
k=(2x2+a)/2y1
若
P
≠
Q
P \neq Q
P=Q,则
k
=
(
y
2
−
y
1
)
/
(
x
2
−
x
1
)
k = (y_2 - y_1)/(x_2 - x_1)
k=(y2−y1)/(x2−x1)
为了方便理解,可以套用以上公式,解决以下例题。
例:已知 E 23 ( 1 , 1 ) E_{23}(1,1) E23(1,1) 上两点 P ( 2 , 10 ) P(2,10) P(2,10), Q ( 9 , 7 ) Q(9,7) Q(9,7),求1) − P -P −P, 2) P + Q P + Q P+Q, 3) 2 P 2P 2P
解:1)
P
(
3
,
10
)
P(3,10)
P(3,10)的负元是
(
3
,
−
10
m
o
d
23
)
=
(
3
,
23
−
10
)
=
(
3
,
13
)
(3, -10 \quad mod \quad 23) = (3, 23 - 10) = (3, 13)
(3,−10mod23)=(3,23−10)=(3,13)
2)
P
≠
Q
,
k
=
(
7
−
10
)
/
(
9
−
3
)
=
−
1
/
2
P \neq Q, k = (7 - 10)/(9 - 3) = -1/2
P=Q,k=(7−10)/(9−3)=−1/2,因为
2
∗
12
≡
1
(
m
o
d
23
)
2 ∗ 12 ≡ 1 (mod \quad 23)
2∗12≡1(mod23),
所以2的乘法逆元为12,
k
≡
−
1
∗
2
−
1
(
m
o
d
23
)
≡
−
1
∗
12
(
m
o
d
23
)
k \equiv -1 * 2^{-1}(mod \quad 23) \equiv -1 * 12(mod \quad 23)
k≡−1∗2−1(mod23)≡−1∗12(mod23),故k=11.
x
3
≡
k
2
−
x
1
−
x
2
(
m
o
d
p
)
≡
1
1
2
−
3
−
9
(
m
o
d
23
)
=
109
(
m
o
d
23
)
≡
17
x_3 \equiv k^2 - x_1 - x_2(mod \quad p) \equiv 11^2 -3 - 9(mod \quad 23) = 109(mod \quad 23) \equiv 17
x3≡k2−x1−x2(modp)≡112−3−9(mod23)=109(mod23)≡17
y
3
≡
k
(
x
1.
−
x
3
)
−
y
1
(
m
o
d
p
)
≡
11
[
3
−
(
−
6
)
]
−
10
(
m
o
d
23
)
=
89
(
m
o
d
23
)
≡
20
y_3 \equiv k(x1. - x3) - y_1(mod \quad p) \equiv 11[3-(-6)] - 10(mod \quad 23) = 89(mod \quad 23) \equiv 20
y3≡k(x1.−x3)−y1(modp)≡11[3−(−6)]−10(mod23)=89(mod23)≡20,故
P
+
Q
P + Q
P+Q 的坐标为
(
17
,
20
)
(17,20)
(17,20)
3)
P
=
Q
P = Q
P=Q,
k
≡
[
3
∗
(
3
2
)
+
1
)
]
/
(
2
+
10
)
(
m
o
d
23
)
=
7
+
5
−
1
(
m
o
d
23
)
k \equiv [3 * (3^2) + 1)] / (2 + 10)(mod \quad 23) = 7 + 5^{-1}(mod \quad 23)
k≡[3∗(32)+1)]/(2+10)(mod23)=7+5−1(mod23) ,
因为
5
∗
14
≡
1
(
m
o
d
23
)
5 * 14 \equiv 1(mod \quad 23)
5∗14≡1(mod23),5的乘法逆元为14,
故k=6。
x
3
≡
k
2
−
x
1
−
x
2
(
m
o
d
p
)
=
6
2
−
3
−
3
(
m
o
d
23
)
=
30
(
m
o
d
23
)
≡
7
x_3 \equiv k^2 - x_1 - x_2(mod \quad p) = 6^2 - 3 - 3(mod \quad 23) = 30(mod \quad 23) \equiv 7
x3≡k2−x1−x2(modp)=62−3−3(mod23)=30(mod23)≡7
y
3
≡
k
(
x
1
−
x
3
)
−
y
1
(
m
o
d
p
)
=
6
∗
(
3
−
7
)
−
10
(
m
o
d
23
)
=
−
34
(
m
o
d
23
)
≡
12
y^3 \equiv k(x_1 - x_3) - y_1(mod \quad p) = 6 * (3 - 7) - 10(mod \quad 23) = -34(mod \quad 23) \equiv 12
y3≡k(x1−x3)−y1(modp)=6∗(3−7)−10(mod23)=−34(mod23)≡12,故
x
P
xP
xP 的坐标为
(
7
,
12
)
(7,12)
(7,12)
4. 椭圆曲线加解密算法原理
设私钥、公钥分别为d、Q,即
Q
=
d
G
Q = dG
Q=dG,其中G为基点,椭圆曲线上的已知G和dG,求d是非常困难的,也就是说已知公钥和基点,想要算出私钥是非常困难的。
公钥加密:选择随机数r,将消息M生成密文C,该密文是一个点对,
C
=
r
G
,
M
+
r
Q
C = {rG, M+rQ}
C=rG,M+rQ,其中Q为公钥。
私钥解密:
M
+
r
Q
−
d
(
r
G
)
=
M
+
r
(
d
G
)
−
d
(
r
G
)
=
M
M + rQ - d(rG) = M + r(dG) - d(rG) = M
M+rQ−d(rG)=M+r(dG)−d(rG)=M,其中d、Q分别为私钥、公钥。
5. 椭圆曲线签名算法原理
椭圆曲线签名算法(ECDSA)。设私钥、公钥分别为d、Q,即 Q = d G Q = dG Q=dG,其中G为基点。
私钥签名:
- 选择随机数r,计算点 r G ( x , y ) rG(x, y) rG(x,y)。
- 根据随机数r、消息M的哈希h、私钥d,计算 s = ( h + d x ) / r s = (h + dx)/r s=(h+dx)/r。
- 将消息M、和签名 r G , s {rG, s} rG,s发给接收方。
公钥验证签名:
- 接收方收到消息M、以及签名 r G = ( x , y ) , s {rG=(x,y), s} rG=(x,y),s。
- 根据消息求哈希h。
- 使用发送方公钥Q计算:
h
G
/
s
+
x
Q
/
s
hG/s + xQ/s
hG/s+xQ/s,并与rG比较,如相等即验签成功。
原理: h G / s + x Q / s = h G / s + x ( d G ) / s = ( h + x d ) G / s = r ( h + x d ) G / ( h + d x ) = r G hG/s + xQ/s = hG/s + x(dG)/s = (h+xd)G/s = r(h+xd)G / (h+dx) = rG hG/s+xQ/s=hG/s+x(dG)/s=(h+xd)G/s=r(h+xd)G/(h+dx)=rG
6. 签名过程
假设要签名的消息是一个字符串:“Hello World!”。DSA签名的第一个步骤是对待签名的消息生成一个消息摘要,不同的签名算法使用不同的消息摘要算法,而ECDSA256使用SHA256生成256比特的摘要。
摘要生成结束后,应用签名算法对摘要进行签名:
- 产生一个随机数k
- 利用随机数k,计算出两个大数r和s。将r和s拼在一起就构成了对消息摘要的签名。
这里需要注意的是,因为随机数k的存在,对于同一条消息,使用同一个算法,产生的签名是不一样的。从函数的角度来理解,签名函数对同样的输入会产生不同的输出。因为函数内部会将随机值混入签名的过程。
7. 验证过程
关于验证过程,这里不讨论它的算法细节。从宏观上看,消息的接收方从签名中分离出r和s,然后利用公开的密钥信息和s计算出r。如果计算出的r和接收到的r值相同,则表示验证成功,否则,表示验证失败。