一、题目

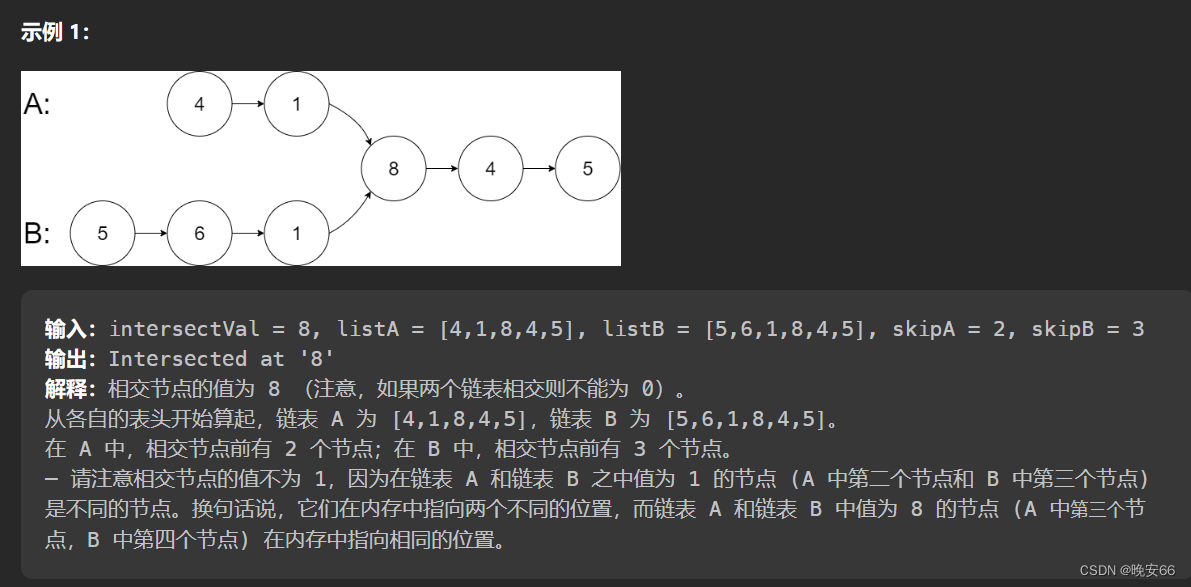
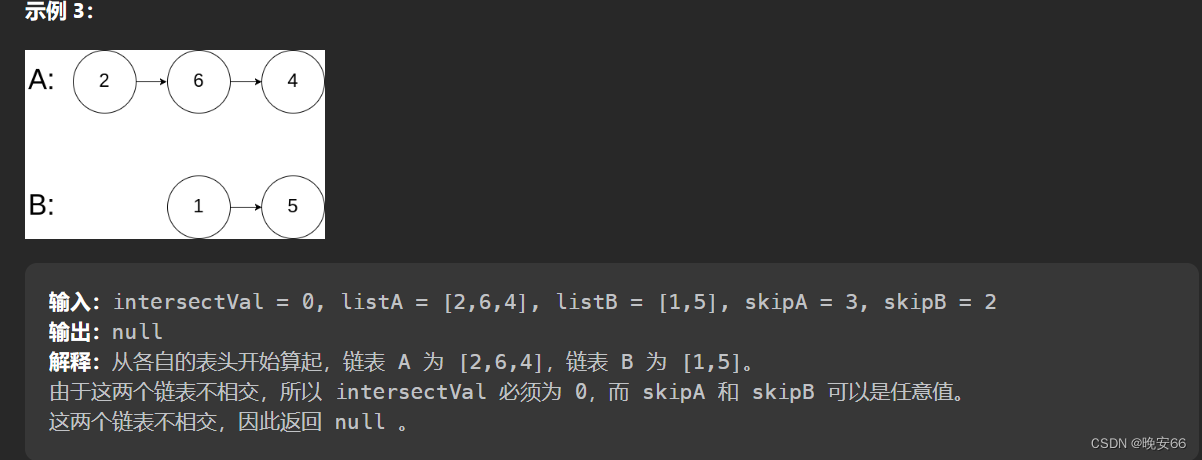
在这里插入图片描述

二、解法

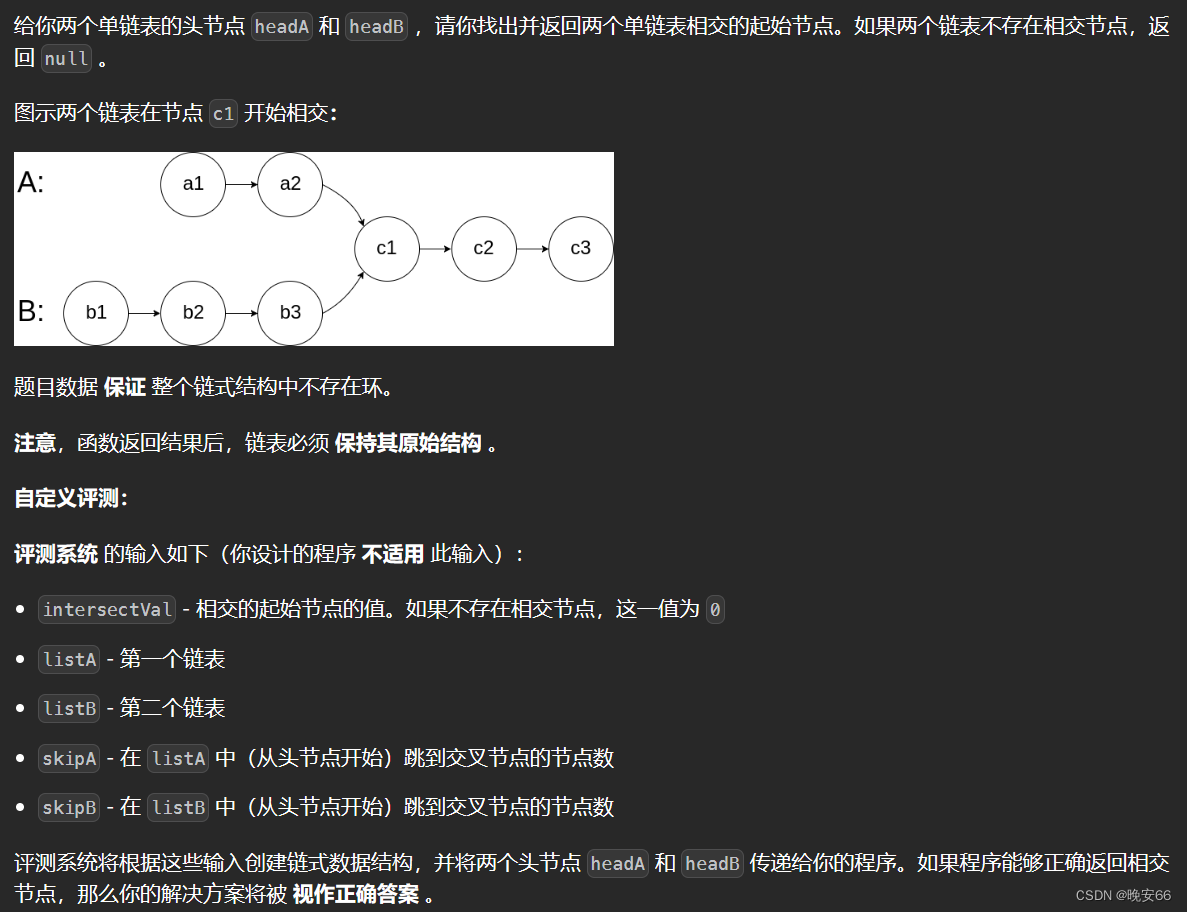
思路分析：这道题题目蛮长的。说的大概意思就是对比指针地址，只要相等了，那就是相交节点。如果设置两个指针挨个遍历两个链表，那么复杂度非常高， $O (m * n)$ 。那么如何达到进阶的要求呢？首先我们要注意到，从相交节点开始，往后的节点是相同的（节点的下一个节点有且仅有一个），此外，链表是有长有短的，意味着长链表第lenB-lenA个节点之前不会是相交节点，那我们就从第lenB-lenA个节点开始查。如图，我们将两个链表分开右对齐放置，依次对比curA curB的地址，直到找到相交节点。关键点在于右对齐放置以后从最后节点开始，往前的节点位置上都是一一对应的，充分利用相交节点往后的节点都是相同节点的特点。
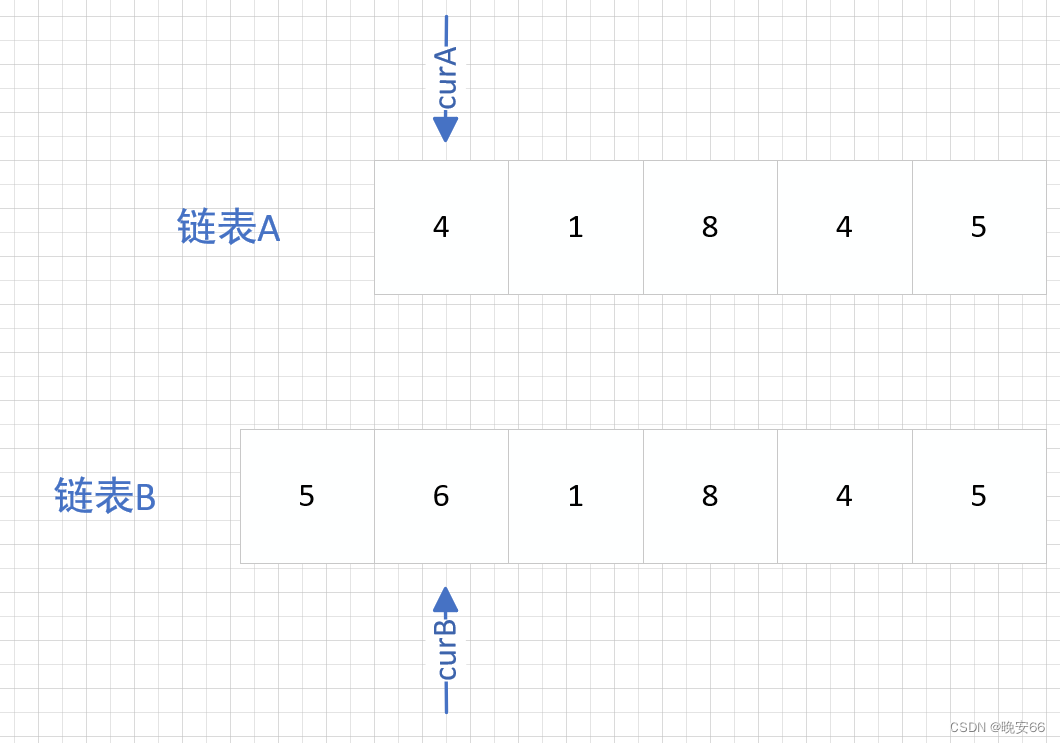
在这里插入图片描述
程序如下：

class Solution {
public:
    ListNode* getIntersectionNode(ListNode* headA, ListNode* headB) {
        ListNode* curA = headA;
        ListNode* curB = headB;
        int lenA = 0;
        int lenB = 0;
        while (curA != NULL) {  // 链表A长度
            curA = curA->next;
            lenA++;
        }
        curA = headB;
        while (curB != NULL) {  // 链表B长度
            curB = curB->next;
            lenB++;
        }
        curA = headA;
        curB = headB;
        if (lenA < lenB) {      // 选出长链表A
            swap(lenA, lenB);
            swap(curA, curB);
        }
        int index = lenA - lenB;
        while (index--) {   // A B链表右对齐
            curA = curA->next;
        }
        while (curA != curB && curA != NULL) {  // 对比地址
            curA = curA->next;
            curB = curB->next;
        }
        return curA == NULL ? NULL : curA;
    }
};

复杂度分析：

时间复杂度： $O (m + n)$ ，用来计算两个链表的长度。
空间复杂度： $O (1)$ 。

三、完整代码

下面代码当中添加了测试主程序，难点在于相交节点的生成。这里我用【算法与数据结构】707、LeetCode设计链表的链表类，重载了addAtIndex将相交节点加进去。

# include <iostream>
using namespace std;

// 定义链表节点类结构体
struct ListNode {
    int val;
    ListNode* next;
    ListNode() : val(0), next(NULL) {};
    ListNode(int input_val) : val(input_val), next(NULL) {};
    ListNode(int input_val, ListNode* input_next) : val(input_val), next(input_next) {};
};

// 链表类
class MyLinkedList {
public:
    // 构造函数
    MyLinkedList() {
        _FakeNode = new ListNode(0, NULL);    // 虚假头结点
        _size = 0;
    }
    // 成员函数
    void addAtIndex(int index, int val);
    void addAtIndex(int index, ListNode* InterNode);
    void ChainGenerator(int arr[], int len);
    void LinkListPrint(string str);
    // 成员变量
    int _size;
    ListNode* _FakeNode;
};

// 在指定位置添加值
void MyLinkedList::addAtIndex(int index, int val) {
    if (index > _size) return;
    if (index < 0) index = 0;
    ListNode* cur = _FakeNode; // 虚结点 
    // 需要断开上一一个阶段的链接，从插入位置的上一个索引开始处理
    while (index--) {
        cur = cur->next;
    }
    ListNode* pNewNode = new ListNode(val, cur->next);
    cur->next = pNewNode;
    _size++;
}

// 重载addAtIndex函数
void MyLinkedList::addAtIndex(int index, ListNode * InterNode) {
    if (index > _size) return;
    if (index < 0) index = 0;
    ListNode* cur = _FakeNode; // 虚结点 
    // 需要断开上一一个阶段的链接，从插入位置的上一个索引开始处理
    while (index--) {
        cur = cur->next;
    }
    InterNode->next = cur->next;
    cur->next = InterNode;
    _size++;
}

void MyLinkedList::ChainGenerator(int arr[], int len) {
    if (_FakeNode->next != NULL) return;
    ListNode* head = new ListNode(arr[0], NULL);
    ListNode* p = head;
    for (int i = 1; i < len; i++) {
        ListNode* pNewNode = new ListNode(arr[i], NULL);
        p->next = pNewNode; // 上一个节点指向这个新建立的节点
        p = pNewNode; // p节点指向这个新的节点
    }
    _FakeNode->next = head;
    _size = len;
}

void MyLinkedList::LinkListPrint(string str) {
    cout << str << endl;
    ListNode* cur = _FakeNode;
    while (cur->next != NULL) {
        cout << cur->next->val << ' ' << cur->next << ' ';
        cur = cur->next;
    }
    cout << endl;
}

class Solution {
public:
    ListNode* getIntersectionNode(ListNode* headA, ListNode* headB) {
        ListNode* curA = headA;
        ListNode* curB = headB;
        int lenA = 0;
        int lenB = 0;
        while (curA != NULL) {  // 链表A长度
            curA = curA->next;
            lenA++;
        }
        curA = headB;
        while (curB != NULL) {  // 链表B长度
            curB = curB->next;
            lenB++;
        }
        curA = headA;
        curB = headB;
        if (lenA < lenB) {      // 选出长链表A
            swap(lenA, lenB);
            swap(curA, curB);
        }
        int index = lenA - lenB;
        while (index--) {   // A B链表右对齐
            curA = curA->next;
        }
        while (curA != curB && curA != NULL) {  // 对比地址
            curA = curA->next;
            curB = curB->next;
        }
        return curA == NULL ? NULL : curA;
    }
};

int main()
{
    int arrA[] = { 4, 1, 4, 5 };
	int lenA = sizeof(arrA) / sizeof(int);
    int arrB[] = { 5, 6, 1, 4, 5 };
	int lenB = sizeof(arrB) / sizeof(int);
    int val = 2;
    ListNode* Node = new ListNode(2, NULL);
    MyLinkedList m1;
    MyLinkedList m2;
    m1.ChainGenerator(arrA, lenA);
    m2.ChainGenerator(arrB, lenB);
    m1.addAtIndex(3, Node);
    m2.addAtIndex(1, Node);
    m1.LinkListPrint("链表A：");
    m2.LinkListPrint("链表B：");
    Solution s1;
	ListNode* InterNode = s1.getIntersectionNode(m1._FakeNode->next, m2._FakeNode->next);
    if (InterNode != NULL) {
        cout << "相交节点的值：" << endl;
        cout << InterNode->val << endl;
    }
	system("pause");
	return 0;
}