原创 | 文 BFT机器人

01 摘要

这篇文章是关于机器人路径跟踪的受控纯追踪算法的研究。文章介绍了传统的纯追踪算法以及相关变体，并提出了受控纯追踪算法作为本文的主要贡献。该算法旨在适应实际环境中的服务和工业移动机器人，提供方法来调整机器人的平移速度以适应当前条件。文章还讨论了该算法在实际机器人系统中的实现和实验验证，并提供了结论。

02 受控纯追踪算法与其他局部轨迹规划技术的不同

受控纯追踪算法是一种局部轨迹规划技术，适用于现实世界中受约束和部分可观测环境中的服务和工业移动机器人。它提供了使机器人的平移速度适应当前条件的方法，例如在急转弯或在受限区域操作时降低速度。该算法使用线性调节成本函数在各种实际的移动机器人环境中提供高质量的行为。与其他局部轨迹规划技术相比，受控纯追踪是专门为移动机器人设计的，并提供了根据当前条件调整速度的方法。

03 受控纯追踪算法的目的是什么

该算法旨在提高服务和工业移动机器人在实际环境中的性能，特别是在受限制和部分可观测的环境中。它提供了一种方法来调整机器人的平移速度以适应当前条件，例如在转弯处或在狭窄区域操作时减少机器人速度。文章还通过实验验证了该算法的有效性，并指出该算法已经被广泛应用于实际机器人系统中。因此，该算法有助于提高服务和工业移动机器人在各种行业中的性能和应用范围。

04 算法的核心是什么？

其核心是通过调整机器人的平移速度以适应当前条件来提高机器人在实际环境中的性能。该算法使用线性调节成本函数来实现这一目标，并提供了高质量的行为，适用于各种实际移动机器人环境。相比传统纯追踪算法，受控纯追踪算法可以更好地适应实际环境，并提高机器人的安全性和效率。因此，该算法的核心是通过调整机器人速度来适应当前环境，从而提高机器人在实际环境中的性能和安全性。

05 论文原理

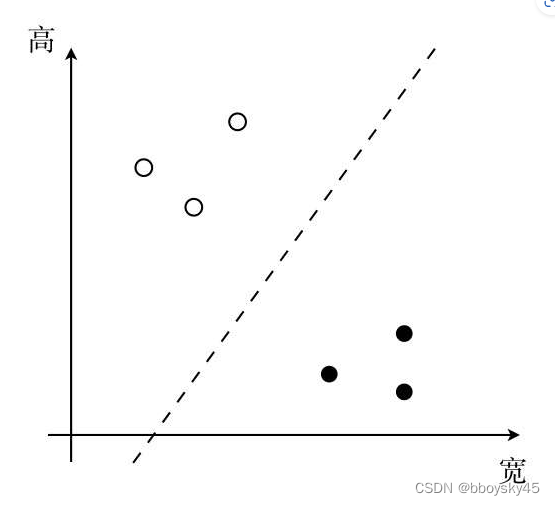
调节纯追求算法的第一阶段是变换输入路径到机器人的基坐标系中并进行修剪。在此过程中，路径曲率的确定被简化为公式1所示的简单代数表达式。

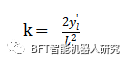
A. 受控纯追踪算法

变换前，确定，所有先前点将从存储路径中永久删除，以防止将来对过时的数据进行不必要的转换。转换后的路径也对所有的点进行修剪，其中，因为它们足够远，在t时不需要考虑它们。这些远路径点继续保存在存储的路径中，以便将来迭代，直到机器人沿着路径前进时接收到新的路径。

接下来，RPP(Regulated Pure Pursuit)将使用与公式2中描述的纯追踪算法相同的前瞻性选择机制。

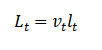
前瞻距离与速度和前视增益成正比，以便在移动更快的同时使用更长的距离，从而不留下误导结果的机会。这在较大的平移速度范围内稳定了路径跟踪行为。该距离用于选择前导点。虽然路径点之间的插值被发现可以明显提高自动驾驶汽车速度下稀疏路径的平滑性，但从经验上看，在使用典型网格地图规划分辨率(0.025 m - 0.1 m)的服务和工业机器人速度下，这并没有带来太大的好处。然而，插值有利于在稀疏路径分辨率(0.1 - 1.0m)中使用。

期望的线速度，接下来由曲率和接近启发式进一步处理。两种启发式方法都适用于线速度，文章中取两者的最大值。

将接近启发式算法应用于机器人接近动态障碍物或固定基础设施时的线速度。这样做的目的是在碰撞可能性特别高的受限环境中减慢机器人的速度。降低固定基础设施附近的速度，通过减少狭小空间中小路径变化的影响，降低碰撞的可能性。

降低工业和服务机器人在接近动态主体(如人类)时的速度是一项常见的安全要求——允许机器人更快地做出反应，以防止潜在的伤害。该启发式的线性公式通过的比值和增益α来降低速度，以调整单个系统的响应。测试的其他公式，如指数和二次公式，对接近物体的惩罚太大，只包含一个狭窄的增益范围，这将导致在接近障碍物和完成机器人任务的速度之间进行可接受的权衡。

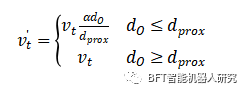
其中是应用启发式算法的障碍物的接近距离，是到障碍物的当前距离，α是缩放攻击行为启发式函数的增益，要求α≤1.0。α值越高，机器人在接近障碍物时的速度越快。的值应该根据机器人应用的系统需求来确定，即在机器人开始放慢其最大速度之前，障碍物可以接近到什么程度。

调整速度后，算法确定路径曲率。角速度是使用调节速度计算的，而不是期望的线速度，这可以防止相对于目标曲率的相应欠冲行为。最后，角速度，可以用公式3简单地求出来。

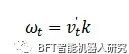
算法的最后一步是检查我们的路径跟踪命令是否有当前或即将发生的碰撞，这是RPP的新功能。给定的角速度和调节的线速度可以在时间上向前投射，得到一个圆弧。弧上的点以网格地图单元分辨率向前采样一段时间。

碰撞检查是基于碰撞的持续时间，而不是基于前瞻点，这样机器人离碰撞总是至少有一段设定的持续时间。在低速行驶时，在几十米或几百秒之外的前方进行碰撞检查可能是不明智的。相反，时间模式允许在有限的空间中进行精细的操作，在这种空间中，当前的速度命令可能在短距离(但长时间)之外不被允许。

B.实验效果

本文提出了一种改进的基于点对特征的点云6D姿态估计方法。该方法提出了一种PCA算法中封闭几何的法向解的方法，并引入了一种通过将体素网格划分为等效角度单元的高效采样方法。最后，采用ICP的变体、基于拟合点的验证步骤和NMS算法进行细化和验证。实验结果表明，该方法具有较高的效率和鲁棒性，平均召回率为0.87。

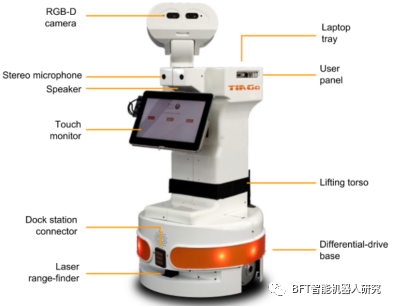
图1 论文实验中使用的机器人

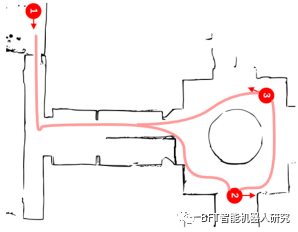
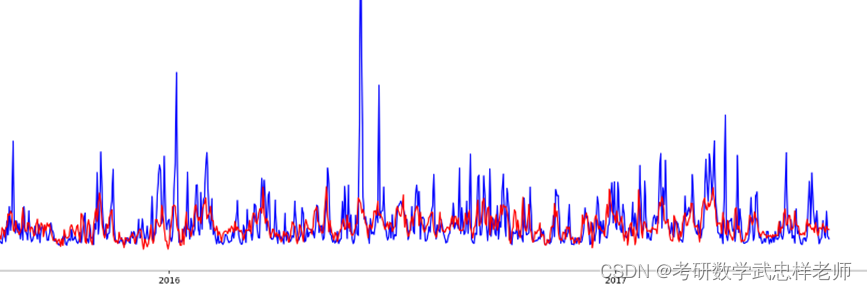
图2 全系统实验行程，全长70米。

机器人将沿着一条路线通过图7所示的校园建筑中的三个控制点。该路线包括无碰撞的开放空间、封闭的大厅和大约70米的盲急转弯。机器人使用每种算法重复三次路径，数据如表3所示。本实验的目的是将RPP算法在系统级的一般行为与现有变体进行比较。

数据表明在整个系统级行为上差别不大——导航的平均时间在85-95秒之间。与之前的实验一致，PP (Pure Pursuit)确实显示了稍短的行进距离和增加的跟踪误差对应于路径抄近路。

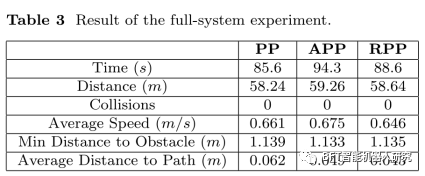
这个实验最引人注目的特点是算法之间缺乏特别独特的结果。尽管RPP在狭窄的走廊和完成急转弯时减慢了机器人的速度，但令人惊讶的是，这些动作对高级导航指标没有显著影响。当考虑到试验之间的标准差时，三种算法的任务完成时间和平均速度是一致的。RPP的系统级性能与APP非常相似，因此我们得出结论，RPP的额外好处对系统设计人员来说几乎没有坏处。

事实上，解决方案架构师可以在使用RPP时适度提高机器人的最大速度，因为它在转弯和靠近障碍物时速度会变慢(机器人应用中速度的常见限制因素)。这大大提高了机器人系统的整体效率，同时确保了更高质量的安全特性。

论文资料：https://arxiv.org/abs/2305.20026  

更多精彩内容请关注公众号：BFT机器人

本文为原创文章，版权归BFT机器人所有，如需转载请与我们联系。若您对该文章内容有任何疑问，请与我们联系，将及时回应。