数列分段 Section II

题目描述

对于给定的一个长度为N的正整数数列 $A_{1\sim N}$，现要将其分成 $M$（$M\le N$）段，并要求每段连续，且每段和的最大值最小。

关于最大值最小：

例如一数列 $42451$ 要分成 $3$ 段。

将其如下分段：

$$[42][45][1]$$

第一段和为 $6$，第 $2$ 段和为 $9$，第 $3$ 段和为 $1$，和最大值为 $9$。

将其如下分段：

$$[4][24][51]$$

第一段和为 $4$，第 $2$ 段和为 $6$，第 $3$ 段和为 $6$，和最大值为 $6$。

并且无论如何分段，最大值不会小于 $6$。

所以可以得到要将数列 $42451$ 要分成 $3$ 段，每段和的最大值最小为 $6$。

输入格式

第 $1$ 行包含两个正整数 $N,M$。

第 $2$ 行包含 $N$ 个空格隔开的非负整数 $A_i$，含义如题目所述。

输出格式

一个正整数，即每段和最大值最小为多少。

样例 #1

样例输入 #1

5 3
4 2 4 5 1

样例输出 #1

6

提示

对于 $20\%$ 的数据，$N\le 10$。

对于 $40\%$ 的数据，$N\le 1000$。

对于 $100\%$ 的数据，$1\le N\le 10^5$，$M\le N$，$A_i<10^8$， 答案不超过 $10^9$。

分析

1. 和上个题一样，二分答案，二分每段和最大值，通过一个check函数断 是否满足当 每段最大值为x时能分m组（<=m即可，不一定非要等于m，因为满足条件的组也可以拆开，来弥补组数一共m组）；
2. 对于check函数，由于题目要求每段连续，所以直接顺序遍历数组，能放进上一组放，不能的话新开一组即可，最后判断当前x下，分组是否<=m；
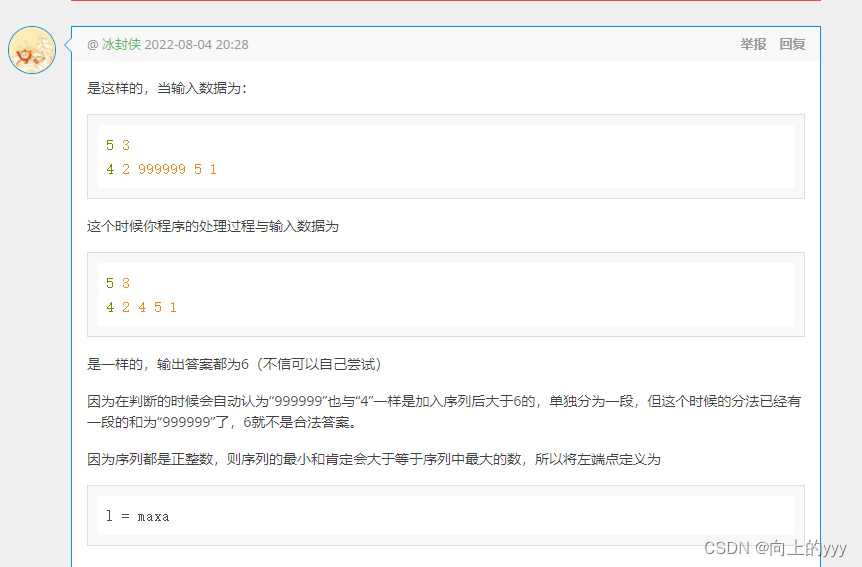
3. 需要注意此题的left、right（取数列的总和）的取值，刚开始left取0，第四个点就WA了，后看题解发现 left的取值为数列中的最大值（一个数为一段），right取数列的总和（所有数为一段）； 二分的区间要以题为准，不能乱设，避免二分的mid实际是非法值，却被进行分组。见下面的大佬评论解释：
   

#include<bits/stdc++.h>

using namespace std;

int n, m, ans;
int a[100010];

//判断是否满足当 每段最大值为x时能分m组
bool check(int x) {
    int cnt = 1;
    int sum = 0;//每组的和
    for (int i = 1; i <= n; ++i) {
        if (sum + a[i] > x) {
            //a[i]需新开一组
            cnt++;
            sum = a[i];
        } else {
            //和上一组同组即可
            sum += a[i];
        }
    }
    return cnt <= m;
}

int main() {
    cin >> n >> m;
    int sum = 0, maxx = 0;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        sum += a[i];
        maxx = max(maxx, a[i]);
    }
    int left = maxx, right = sum, mid;
    while (left <= right) {
        mid = left + (right - left) / 2;
        if (check(mid)) {
            //每段最大值可以更小
            ans = mid;
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    cout << ans;
    return 0;
}