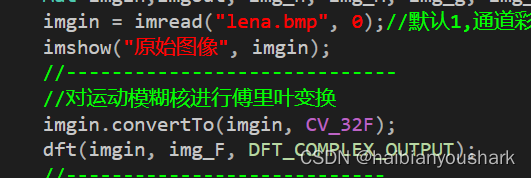
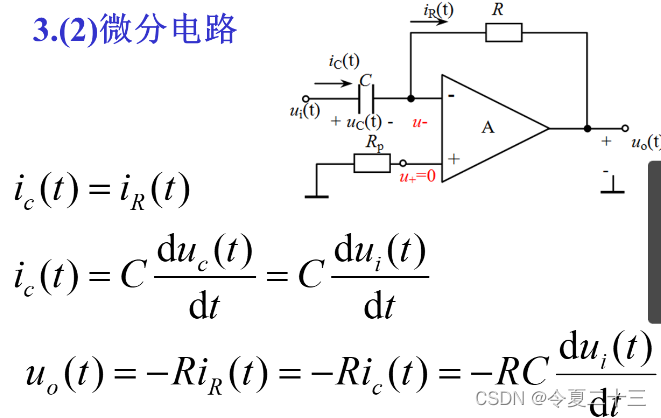
函数声明： 

#include <stdio.h>
#include <math.h>

#define MAXSIZE 200
#define N 8

typedef struct          //栈的存储结构
{
    int data[MAXSIZE];
    int MD[MAXSIZE];
    int top;
}stack1;

void stackinitiate(stack1 *s);          //初始化栈
void push (stack1 *s,int e,int n) ;     //入栈
int getlines(int md);                     //获得行
int getrow(int md); 					 //获得列
int getbinary(int md); 					//由十进制MD码，获得二进制MD码
void pri(int (*p)[N]);					//打印二维数组

算法实现： 

int main()
{
	int v[N][N];
	stack1 a={{0,1,0,2,4,2,2,0,0,2,2,0,0,0,0,4},{0,4,8,12,16,32,33,34,35,36,37,38,39,40,44,48},16};   //讲PPT上的示例数据填入栈内
	stack1 b;
	stackinitiate(&b);
	for(int i=0;i<a.top;i++)
	{
		if(i==a.top-1){                           //如果到达栈的底部
			int value=N*N-a.MD[i];                //获得压缩数量
			for(int h=0;h<value;h++){               //剩余全部入栈b
				push(&b,a.MD[i]+h,a.data[i]);
			}
		 }
	    if((a.MD[i])+1!=a.MD[i+1]){               //如果第i位MD码，和第i+1位MD码不相邻
			int value=a.MD[i+1]-a.MD[i];       //获取中间压缩数量
			for(int j=0;j<value;j++){             //补齐
				push(&b,a.MD[i]+j,a.data[i]);
			}
	     }
		  if(a.MD[i]+1==a.MD[i+1]){                    //如果第i位MD码，和第i+1位MD码相邻，第i位从a栈入栈b
			push(&b,a.MD[i],a.data[i]);
		 }	 
    }

	for(int i=0;i<b.top;i++){            //将b栈的数据从栈顶按MD码大小顺序存放入二维数组v中
		int md=getbinary(b.MD[i]);
		int x=getlines(md);
		int y=getrow(md);
		v[x][y]=b.data[i];
		printf("%d",v[x][y]);
	}

	printf("\n\n"); 
	 
	pri(v);           //打印二维数组
	return 0;
}

 函数实现：

void push (stack1 *s,int e,int n)         //入栈
{
	s->MD[s->top]=e;
	s->data[s->top]=n;
	s->top++;
	
}

int getlines(int md)             //获得行
{
	int res=0;
	int i=0;
	while(md){
		md/=10;
		res+=md%10*pow(2,i++);
		md/=10;
	}
	return res;
}

int getrow(int md)				 //获得列
{
	int res=0;
	int i=0;
	while(md){
		res+=md%10*pow(2,i++);
		md/=100;
	}
	return res;
}

int getbinary(int md)            //获得二进制MD码
{
	double res=0;
	int i=0;
	while(md){
		int temp=md%2;
		res+=temp*pow(10,i++);
		md=md/2;
	}
	return res;
}

void pri(int (*p)[N])                 //打印
{
	for(int i=0;i<N-1;i++){
		for(int j=0;j<N-1;j++){
			printf("%d,",p[i][j]);
		}
		printf("\n");
	}
}

void stackinitiate(stack1 *s)             //初始化栈
{
	s->top=0;
}

 结果:

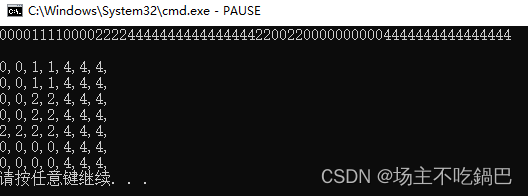
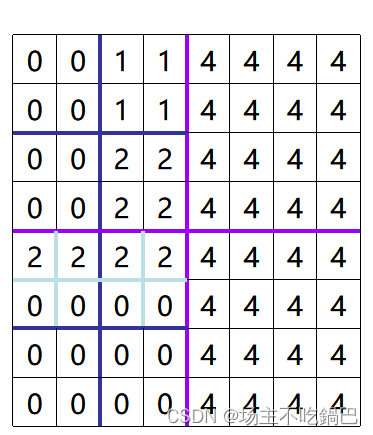
中间的函数是用蠢方法写出来的，位运算的实现在这:http://t.csdn.cn/4rUDA