11.1 数制与数制转换

11.2 二进制数的编码

1. 二-十进制（BCD）码

把十进制数的每一位用多位二进制数表示，称为二进制编码的十进制数，简称BCD编码。

具有二进制数的形式，又具有十进制数的特点。

2. 8421码

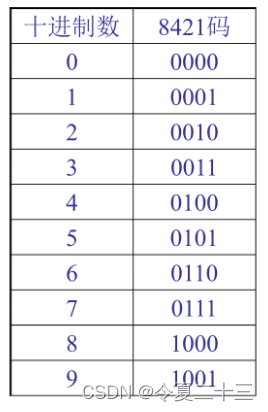
 3. 2421码

 4. 奇偶校验码

 11.3 逻辑代数

1和0是二值布尔代数，也就是开关代数，用于表示电路的开合。

布尔代数是数字逻辑电路分析和设计的基础，又称逻辑代数。

11.3.1 基本逻辑

基本逻辑的逻辑符号

      “与”逻辑符号                      “或”逻辑符号                    “非”逻辑符号

 11.3.2 基本逻辑运算

基本逻辑运算：逻辑加、逻辑乘、逻辑非

复合逻辑运算：逻辑与非（先与再非），逻辑或非（先或再非），逻辑与或非（先与再或最后整体非）

 

 

11.3.3 逻辑函数与真值表

由真值表推到逻辑函数

方法一：

 

 方法二：

 

 11.3.4 逻辑函数的基本定理

 基本逻辑运算都满足交换律、结合律和分配律。

另外，还有一些特殊规律：

 

 

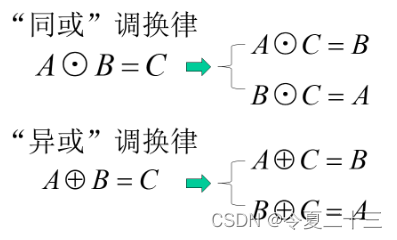
 11.3.5 三个规则

1. 代入规则

2. 反演规则

 3. 对偶规则

相较于反演规则，得到对偶函数不需要将变量取反，只需要对“·”和“+”、“0”和“1”取反即可。

 11.3.6 常用公式

 11.3.7 逻辑函数的标准形式

由真值表写出逻辑函数表达式有两种标准形式：最小项表达式和最大项表达式。

1. 最小项和最大项

在n个变量的逻辑函数中，若m为包含n个因子的乘积项，而且这n个因子均以原变量或反变量的形式在m中出现一次，则称m为该组变量的最小项。

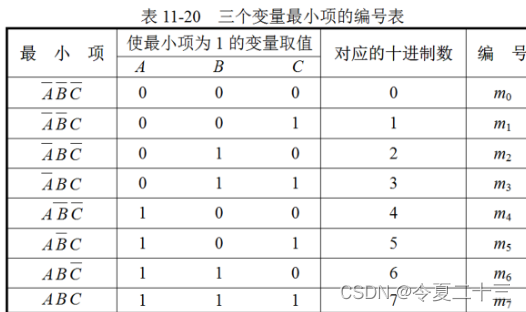
 最小项的性质：

 在n个变量的逻辑函数中，若M为n个变量之和，而且这n个变量均以原变量或反变量的形式在M中出现一次，则称M为该组变量的最大项。

 最大项性质：

 2. 最小项表达式

1）配项法

2）真值表法

 3. 最大项表达式

 11.4 逻辑函数的化简

11.4.1 代数化简法

合并项法、吸收法，配项法

消去法：

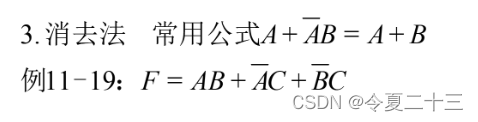
 11.4.2 卡诺图法

代数化简法不太方便，有时不易化到最简，

卡诺图是根据真值表，按一定规律画出来的方格图。

1. 卡诺图的画法——三条原则

 

 

 

 卡诺图中的每个方块都对应一个最小项

11.4.3 卡诺图化简法

1. 用卡诺图表示逻辑函数

1）根据真值表填写卡诺图，将函数值填入卡诺图相应的方块中，一般情况下，0不填，留白。

2）根据最小项之和的式子填写卡诺图；

3）观察简单表达式，思考其值为1时，卡诺图的填写内容。

2. 逻辑函数的卡诺图化简法

画卡诺圈（处于边缘的对称格也可以画，同一个格子也可以被圈多次），最好是4的倍数，也可以单独或者两个，但是尽量避免，最后可以得到合并结果。

11.4.4 具有约束条件逻辑函数的化简

“约束”：在逻辑功能中不可能出现的逻辑变量组合，又称为“无关项”。

化简时，无关项可以作为“1”，也可以作为“0”，在卡诺图中可以当作1，使得化简更简单。

无关项在真值表和卡诺图中用X表示。