目录
73. 矩阵置零 Set Matrix Zeroes 🌟🌟
74. 搜索二维矩阵 Search A 2d-Matrix 🌟🌟
75. 颜色分类 Sort Colors 🌟🌟
🌟 每日一练刷题专栏 🌟
Rust每日一练 专栏
Golang每日一练 专栏
Python每日一练 专栏
C/C++每日一练 专栏
Java每日一练 专栏
73. 矩阵置零 Set Matrix Zeroes
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用原地算法。
示例 1:
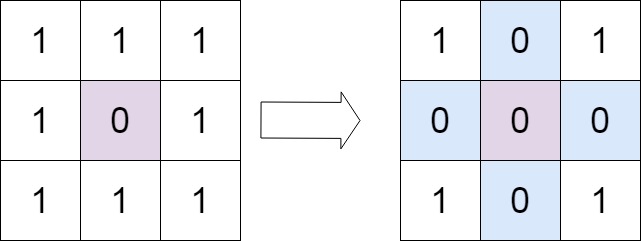
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:
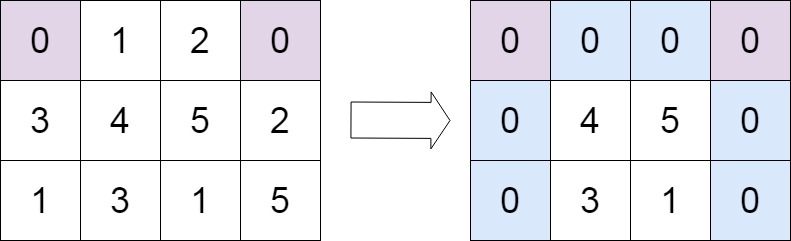
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]] 输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
m == matrix.lengthn == matrix[0].length1 <= m, n <= 200-2^31 <= matrix[i][j] <= 2^31 - 1
进阶:
- 一个直观的解决方案是使用
O(mn)的额外空间,但这并不是一个好的解决方案。 - 一个简单的改进方案是使用
O(m+n)的额外空间,但这仍然不是最好的解决方案。 - 你能想出一个仅使用常量空间的解决方案吗?
代码1:
fn set_zeroes(matrix: &mut Vec<Vec<i32>>) {
let m = matrix.len();
let n = matrix[0].len();
let mut row = vec![false; m];
let mut col = vec![false; n];
for i in 0..m {
for j in 0..n {
if matrix[i][j] == 0 {
row[i] = true;
col[j] = true;
}
}
}
for i in 0..m {
for j in 0..n {
if row[i] || col[j] {
matrix[i][j] = 0;
}
}
}
}
fn main() {
let mut matrix = vec![vec![1, 1, 1], vec![1, 0, 1], vec![1, 1, 1]];
set_zeroes(&mut matrix);
println!("{:?}", matrix);
matrix = vec![vec![0, 1, 2, 0], vec![3, 4, 5, 2], vec![1, 3, 1, 5]];
set_zeroes(&mut matrix);
println!("{:?}", matrix);
}
输出:
[[1, 0, 1], [0, 0, 0], [1, 0, 1]]
[[0, 0, 0, 0], [0, 4, 5, 0], [0, 3, 1, 0]]
代码2:
fn set_zeroes(matrix: &mut Vec<Vec<i32>>) {
let m = matrix.len();
let n = matrix[0].len();
let mut row0 = false;
let mut col0 = false;
for i in 0..m {
for j in 0..n {
if matrix[i][j] == 0 {
if i == 0 {
row0 = true;
}
if j == 0 {
col0 = true;
}
matrix[0][j] = 0;
matrix[i][0] = 0;
}
}
}
for i in 1..m {
for j in 1..n {
if matrix[i][0] == 0 || matrix[0][j] == 0 {
matrix[i][j] = 0;
}
}
}
if row0 {
for j in 0..n {
matrix[0][j] = 0;
}
}
if col0 {
for i in 0..m {
matrix[i][0] = 0;
}
}
}
fn main() {
let mut matrix = vec![vec![1, 1, 1], vec![1, 0, 1], vec![1, 1, 1]];
set_zeroes(&mut matrix);
println!("{:?}", matrix);
matrix = vec![vec![0, 1, 2, 0], vec![3, 4, 5, 2], vec![1, 3, 1, 5]];
set_zeroes(&mut matrix);
println!("{:?}", matrix);
}74. 搜索二维矩阵 Search A 2d-Matrix
编写一个高效的算法来判断 m x n 矩阵中,是否存在一个目标值。该矩阵具有如下特性:
- 每行中的整数从左到右按升序排列。
- 每行的第一个整数大于前一行的最后一个整数。
示例 1:
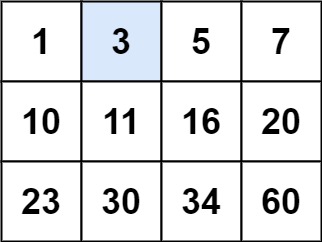
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3 输出:true
示例 2:
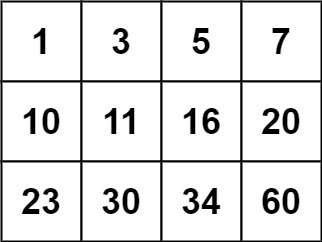
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13 输出:false
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-10^4 <= matrix[i][j], target <= 10^4
代码1:
fn search_matrix(matrix: &Vec<Vec<i32>>, target: i32) -> bool {
let m = matrix.len();
let n = matrix[0].len();
let mut l = 0;
let mut r = m * n - 1;
while l <= r {
let mid = (l + r) >> 1;
if matrix[mid / n][mid % n] == target {
return true;
} else if matrix[mid / n][mid % n] < target {
l = mid + 1;
} else {
r = mid - 1;
}
}
false
}
fn main() {
let matrix = vec![vec![1, 3, 5, 7], vec![10, 11, 16, 20], vec![23, 30, 34, 60]];
println!("{}", search_matrix(&matrix, 3));
println!("{}", search_matrix(&matrix, 13));
}输出:
true
false
代码2:
fn search_matrix(matrix: &Vec<Vec<i32>>, target: i32) -> bool {
let m = matrix.len();
let n = matrix[0].len();
let (mut l, mut r) = (0, m - 1);
while l <= r {
let mid = (l + r) >> 1;
if matrix[mid][0] == target {
return true;
} else if matrix[mid][0] < target {
l = mid + 1;
} else {
r = mid - 1;
}
}
let row = r;
let (mut l, mut r) = (0, n - 1);
while l <= r {
let mid = (l + r) >> 1;
if matrix[row][mid] == target {
return true;
} else if matrix[row][mid] < target {
l = mid + 1;
} else {
r = mid - 1;
}
}
false
}
fn main() {
let matrix = vec![vec![1, 3, 5, 7], vec![10, 11, 16, 20], vec![23, 30, 34, 60]];
println!("{}", search_matrix(&matrix, 3));
println!("{}", search_matrix(&matrix, 13));
}75. 颜色分类 Sort Colors
给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库的sort函数的情况下解决这个问题。
示例 1:
输入:nums = [2,0,2,1,1,0] 输出:[0,0,1,1,2,2]
示例 2:
输入:nums = [2,0,1] 输出:[0,1,2]
提示:
n == nums.length1 <= n <= 300nums[i]为0、1或2
进阶:
- 你可以不使用代码库中的排序函数来解决这道题吗?
- 你能想出一个仅使用常数空间的一趟扫描算法吗?
代码1:
fn sort_colors(nums: &mut Vec<i32>) {
let mut count = vec![0; 3];
for &num in nums.iter() {
count[num as usize] += 1;
}
let mut index = 0;
for i in 0..3 {
for _ in 0..count[i] {
nums[index] = i as i32;
index += 1;
}
}
}
fn main() {
let mut nums = vec![2, 0, 2, 1, 1, 0];
sort_colors(&mut nums);
println!("{:?}", nums);
nums = vec![2, 0, 1];
sort_colors(&mut nums);
println!("{:?}", nums);
}代码2:
fn sort_colors(nums: &mut Vec<i32>) {
let mut index = 0;
for i in 0..nums.len() {
if nums[i] == 0 {
nums.swap(i, index);
index += 1;
}
}
for i in index..nums.len() {
if nums[i] == 1 {
nums.swap(i, index);
index += 1;
}
}
}
fn main() {
let mut nums = vec![2, 0, 2, 1, 1, 0];
sort_colors(&mut nums);
println!("{:?}", nums);
nums = vec![2, 0, 1];
sort_colors(&mut nums);
println!("{:?}", nums);
}代码3:
fn sort_colors(nums: &mut Vec<i32>) {
let (mut left, mut right) = (0, nums.len() - 1);
let mut i = 0;
while i <= right {
if nums[i] == 0 {
nums.swap(i, left);
left += 1;
i += 1;
} else if nums[i] == 2 {
nums.swap(i, right);
right -= 1;
} else {
i += 1;
}
}
}
fn main() {
let mut nums = vec![2, 0, 2, 1, 1, 0];
sort_colors(&mut nums);
println!("{:?}", nums);
nums = vec![2, 0, 1];
sort_colors(&mut nums);
println!("{:?}", nums);
}输出:
[0, 0, 1, 1, 2, 2]
[0, 1, 2]
🌟 每日一练刷题专栏 🌟
✨ 持续,努力奋斗做强刷题搬运工!
👍 点赞,你的认可是我坚持的动力!
🌟 收藏,你的青睐是我努力的方向!
✎ 评论,你的意见是我进步的财富!
☸ 主页:https://hannyang.blog.csdn.net/
|
| Rust每日一练 专栏(2023.5.16~)更新中... |
|
| Golang每日一练 专栏(2023.3.11~)更新中... |
|
| Python每日一练 专栏(2023.2.18~2023.5.18)暂停更 |
|
| C/C++每日一练 专栏(2023.2.18~2023.5.18)暂停更 |
|
| Java每日一练 专栏(2023.3.11~2023.5.18)暂停更 |