因为数组是环形的，所以子数组最大和有两种情况：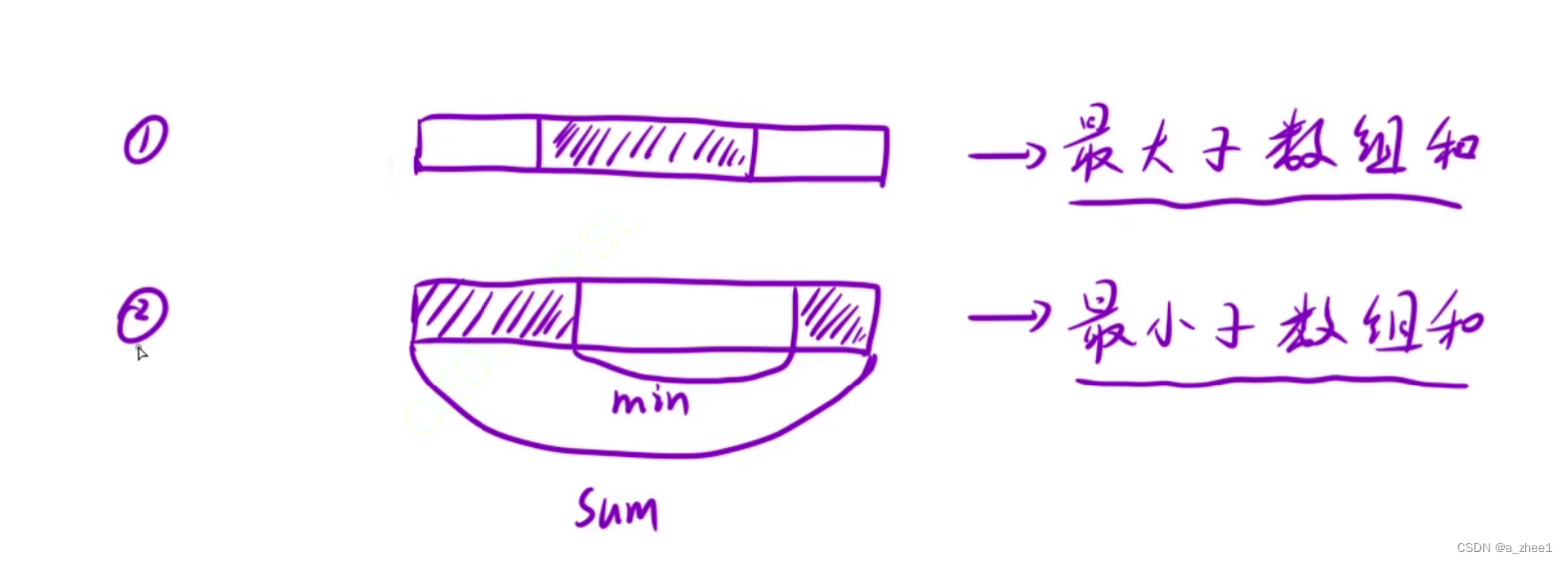

 一个数组内所以数的和是固定的，如果阴影部分是最大子数组和，那么空白部分就是最小子数组和，因此：第二种情况下，只需要求得最小子数组和，再用sum - min，就能得到最大子数组和。

1.状态表示

是什么？dp表中里的值所表示的含义就是状态表示

创建两个dp表，分别存储  最大子数组和  和  最小子数组和

f[i]表示：以i位置为结尾的所有子数组中的最大和

g[i]表示：以i位置为结尾的所有子数组中的最小和

2.状态转移方程

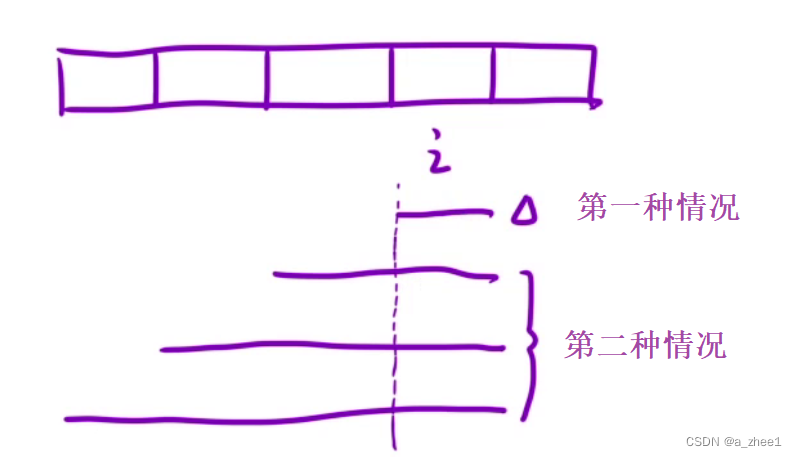
 i位置分为两种情况分别是：长度等于1，长度大于1

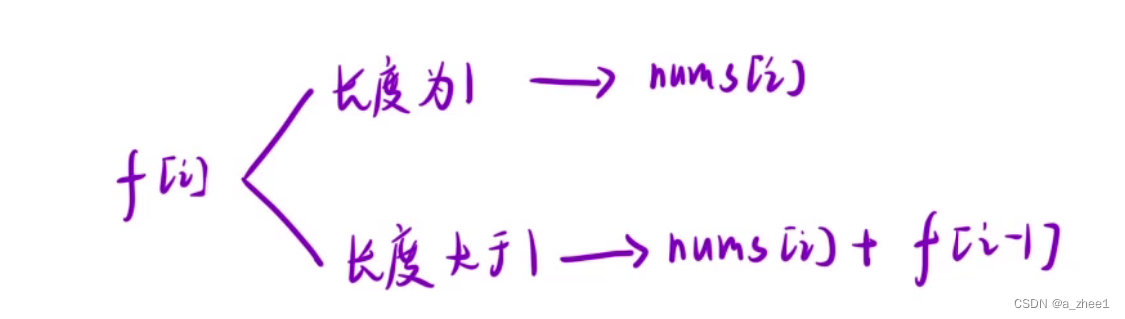
 f[i] = max(nums[i] , nums[i]+f[i-1]);

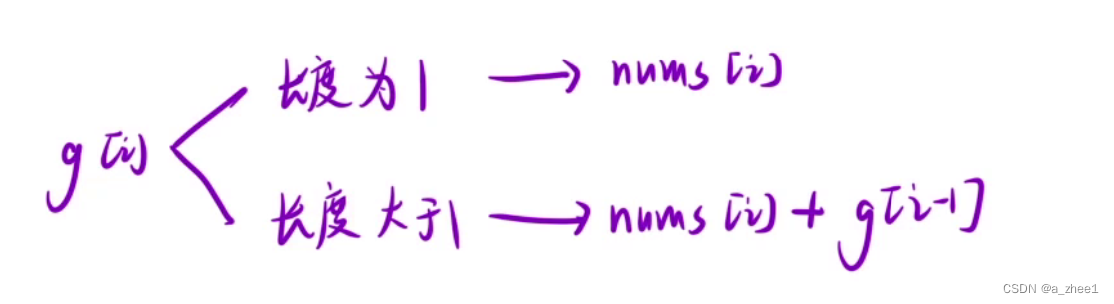
  g[i] = min(nums[i] , nums[i]+g[i-1]);

3.初始化

保证填表的时候不越界

 创建一个虚拟节点，存0，不会影响后续填表

4.填表顺序

为了填写当前状态的时候，所需要的状态已经计算过了

从左往右

5.返回值

题目要求+状态表示

正常情况下，我们只需要返回（f表里的最大值） 和 （sum - g表里的最小值）中的最大值

但是，如给的表里全是负数，这样就会返回0（sum - g表里的最小值）

显然这样是错误的

所以我们要做出判断，当 sum - g表里的最小值 == 0 时，应该返回f表里的最大值

6.代码

class Solution {
public:
    int maxSubarraySumCircular(vector<int>& nums) {
        int n = nums.size();
        //1.创建dp表
        vector<int> f(n+1);
        vector<int> g(n+1);
        //2.初始化
        f[0] = g[0] = 0;
        //3.填表
        int sum = 0;
        for(int i = 1;i < n+1;i++)
        {
            f[i] = max(nums[i-1] , nums[i-1]+f[i-1]);
            g[i] = min(nums[i-1] , nums[i-1]+g[i-1]);
            sum += nums[i-1];
        }
        //4.返回值
        int retf = INT_MIN;
        int retg = INT_MAX;
        for(int j = 1;j < n+1;j++)
        {
            retf = max(retf,f[j]);
            retg = min(retg,g[j]);
        }
        if(sum - retg == 0)
        {
            return retf;
        }
        return max(sum - retg,retf);
    }
};