0. 题目

1. T1
T1.1 绘制阻尼因子曲线
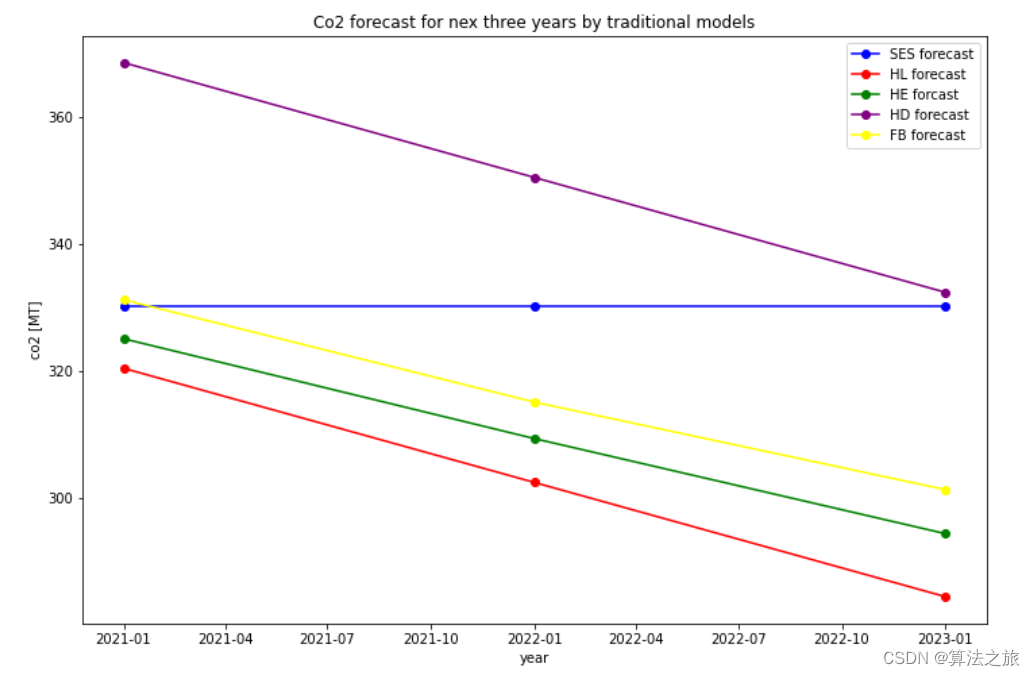
将尝试次数和lambda保存为csv,绘制成曲线如下图
iter, lambda
1, 0.002000
2, 0.008000
3, 0.064000
4, 1.024000
5, 32.768000
6, 2097.152000
7, 699.050667
8, 1398.101333
9, 5592.405333
10, 1864.135111
11, 1242.756741
12, 414.252247
13, 138.084082
14, 46.028027
15, 15.342676
16, 5.114225
17, 1.704742
18, 0.568247
19, 0.378832
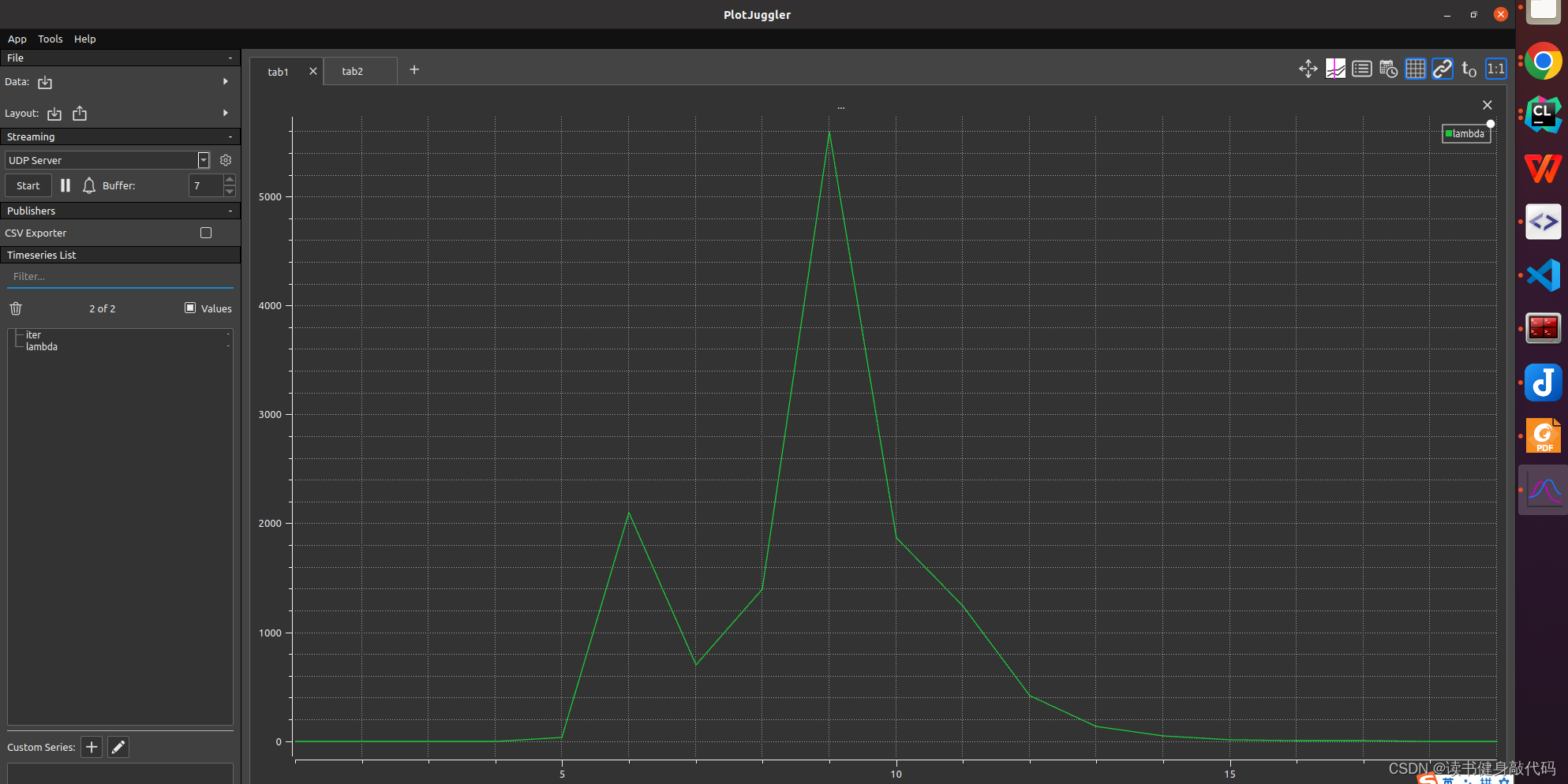
发现起始时刻的
μ
\mu
μ较小,步长
Δ
x
\Delta x
Δx较大,导致cost上升,并未收敛,根据Nielsen策略,迅速调大
μ
\mu
μ,在求解
H
Δ
X
=
b
H \Delta X=b
HΔX=b时减小步长,不断迭代,在迭代过程中逐渐减小
μ
\mu
μ以增大步长加快收敛速度,满足优化终止条件之后停止优化(本题停止条件之一是误差下降超过1e6倍则停止优化)。
T1.2 更改目标函数
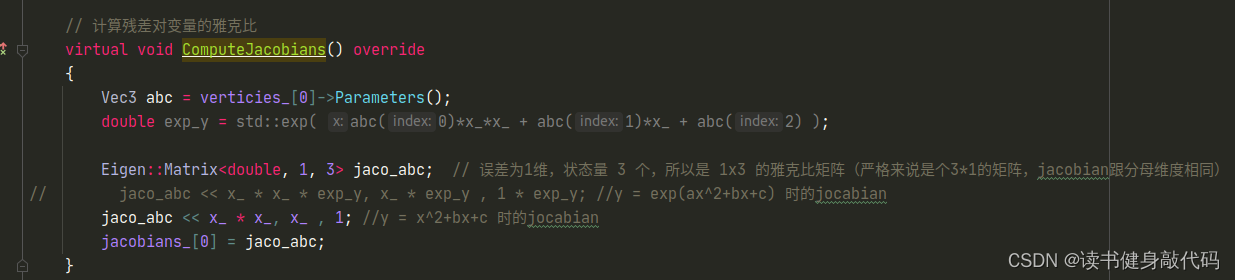
3处修改:
- 修改函数:
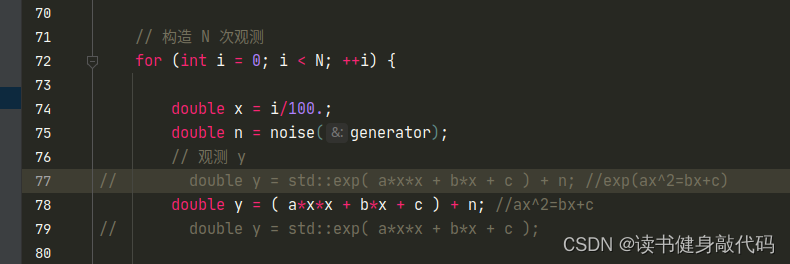
- 修改residual

- 修改Jocabian
但是修改完之后发现拟合效果并不好,原观测数据服从 N ( 0 , 1 ) N(0,1) N(0,1)的正态分布,但是从 e x p ( a x 2 + b x + c ) exp(ax^2+bx+c) exp(ax2+bx+c)修改为 a x 2 + b x + c ax^2+bx+c ax2+bx+c之后, σ = 1 \sigma=1 σ=1显得有些大了(这个应该能从exp和二次函数的曲线分析出来,x正半轴二次函数比exp上升更快,真值相对于噪声观测值的误差也变得越大),所以要想获得更好的曲线拟合效果:1. 增加数据量;2. 减小噪声的variance以下是一些对比:
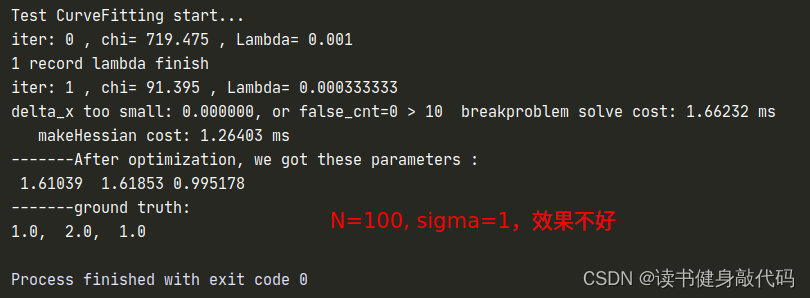
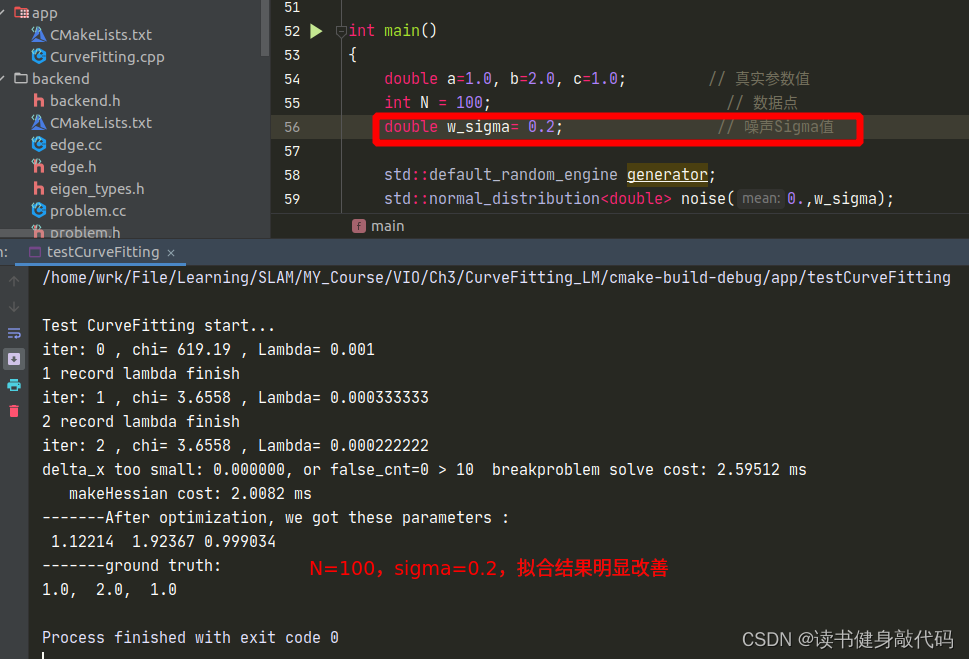
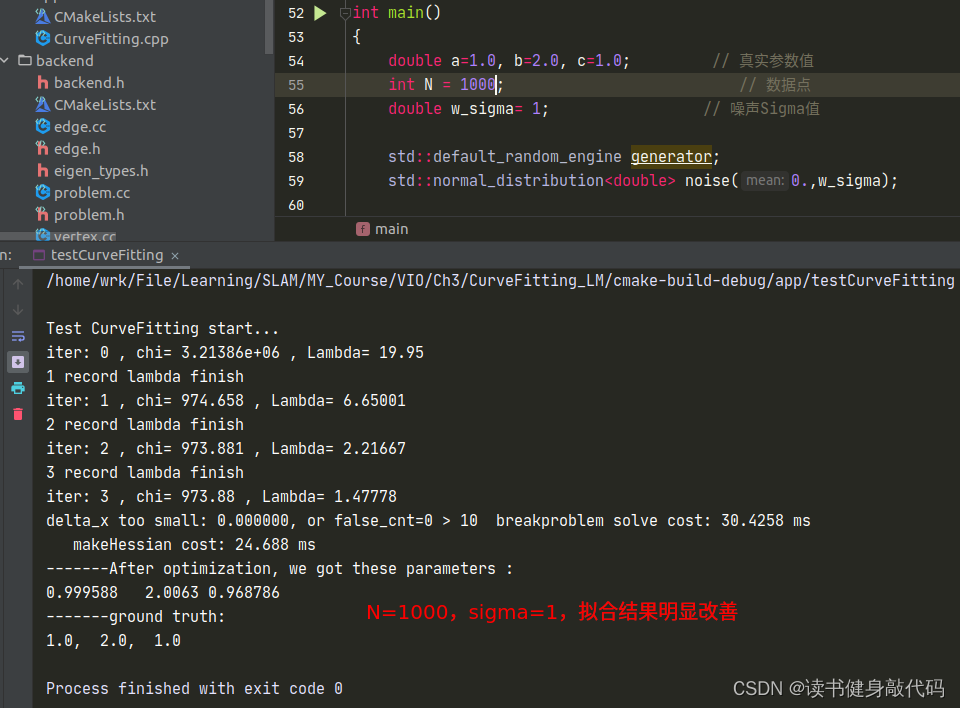
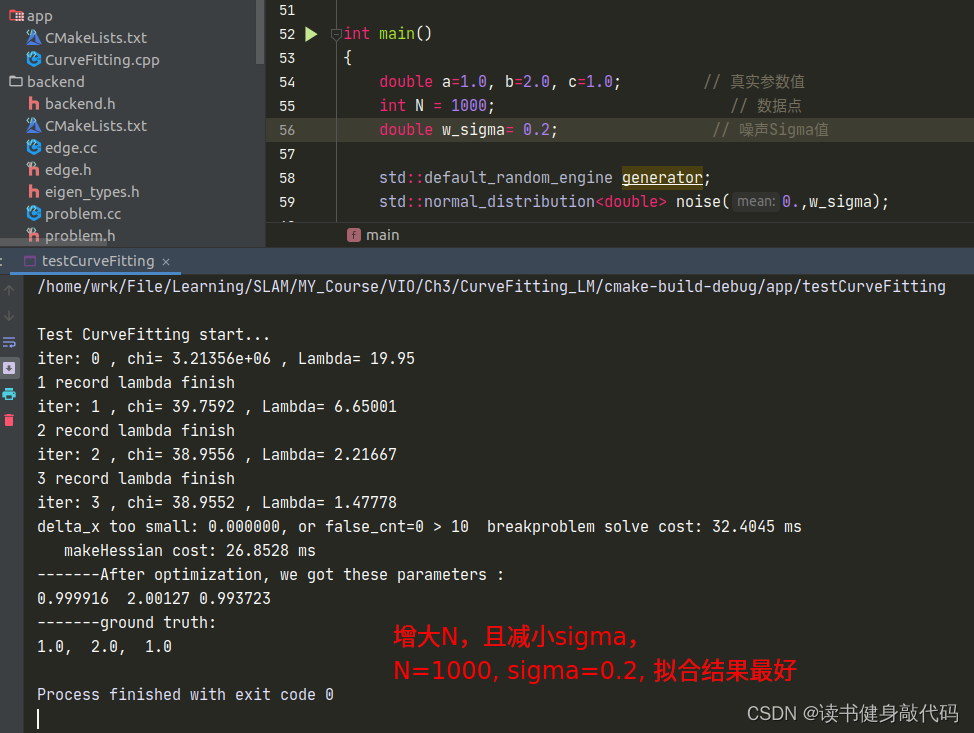
T1.3 不同的LM阻尼因子μ设置策略
参考论文 Henri Gavin. “The Levenberg-Marquardt method for nonlinear least squares curve-fitting problems”. In:Department of Civil and Environmental Engineering, Duke University (2011), pp. 1–15. 的4.1.1节:

使用T1.2中的N=1000,
σ
=
0.2
\sigma=0.2
σ=0.2的参数进行实验。
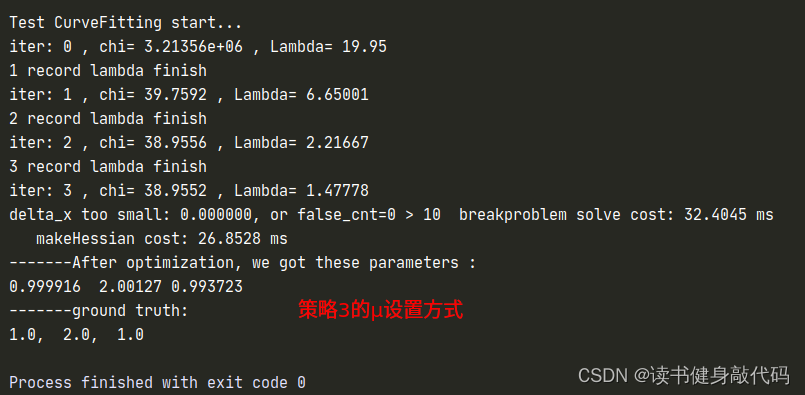
1.3.1 策略3
第三种方法显然是Nelsion的设置方法,
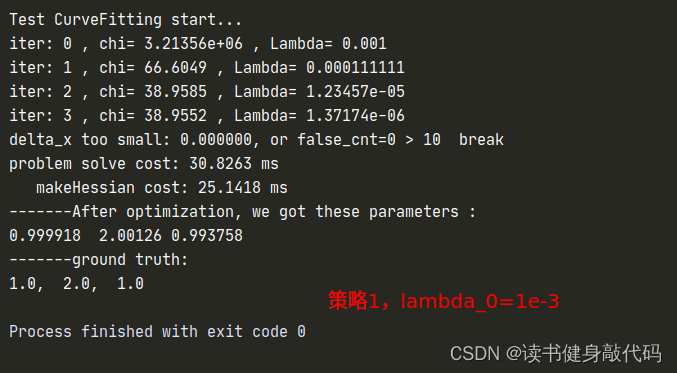
1.3.2 策略1
函数ComputeLambdaInitLM()
currentLambda_ = 1e-3; //选择不同的初值来实验
// currentLambda_ = 1e3;
// set a large value, so that first updates are small steps in the steepest-descent direction
增减 λ \lambda λ:
void Problem::AddLambdatoHessianLM() {
ulong size = Hessian_.cols();
assert(Hessian_.rows() == Hessian_.cols() && "Hessian is not square");
for (ulong i = 0; i < size; ++i) {
// Hessian_(i, i) += currentLambda_;
Hessian_(i, i) += currentLambda_ * Hessian_(i, i); //理解: H(k+1) = H(k) + λ H(k) = (1+λ) H(k)
}
}
void Problem::RemoveLambdaHessianLM() {
ulong size = Hessian_.cols();
assert(Hessian_.rows() == Hessian_.cols() && "Hessian is not square");
// TODO:: 这里不应该减去一个,数值的反复加减容易造成数值精度出问题?而应该保存叠加lambda前的值,在这里直接赋值
for (ulong i = 0; i < size; ++i) {
// Hessian_(i, i) -= currentLambda_;
Hessian_(i, i) /= 1.0 + currentLambda_;//H回退: H(k) = 1/(1+λ) * H(k+1)
}
}
判断 λ \lambda λ是否好:
bool Problem::IsGoodStepInLM() {
// 统计所有的残差
double tempChi = 0.0;
for (auto edge: edges_) {
edge.second->ComputeResidual();
tempChi += edge.second->Chi2();//计算cost
}
assert(Hessian_.rows() == Hessian_.cols() && "Hessian is not square");
ulong size = Hessian_.cols();
MatXX diag_hessian(MatXX::Zero(size, size));
for(ulong i = 0; i < size; ++i) {
diag_hessian(i, i) = Hessian_(i, i);
}
double scale = delta_x_.transpose() * (currentLambda_ * diag_hessian * delta_x_ + b_);//scale就是rho的分母
double rho = (currentChi_ - tempChi) / scale;//计算rho
// update currentLambda_
double epsilon = 0.75;
double L_down = 9.0;
double L_up = 11.0;
if(rho > epsilon && isfinite(tempChi)) {
currentLambda_ = std::max(currentLambda_ / L_down, 1e-7);
currentChi_ = tempChi;
return true;
} else {
currentLambda_ = std::min(currentLambda_ * L_up, 1e7);
return false;
}
}
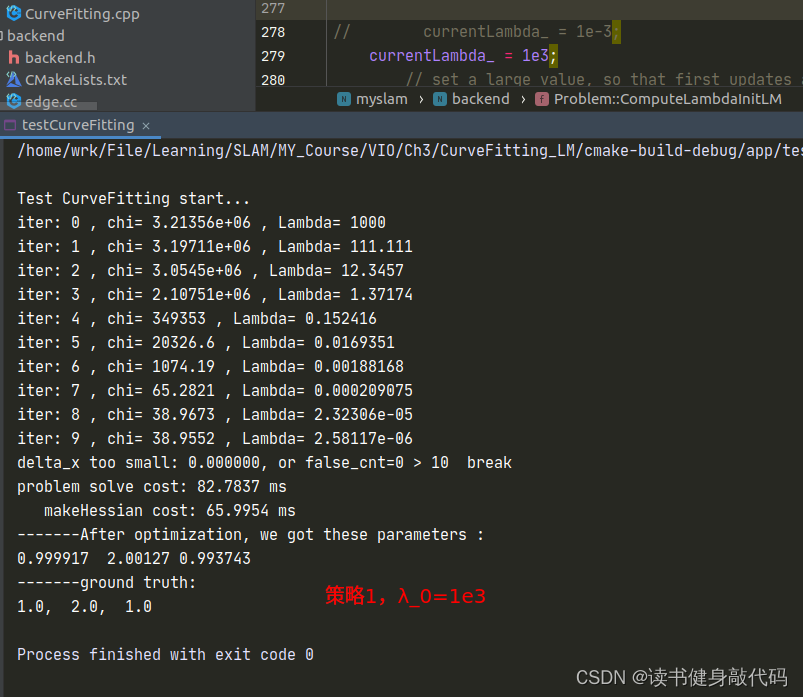
以上对比实验参考:https://note.youdao.com/ynoteshare/index.html?id=15a9ff86fedeb41d92f182e5cb3bace7&type=notebook&_time=1686390423162#/WEBbbb1c7ce04945f67a58c304455a56eda
但是得到了相反的结果,所以其结论我认为并不完全可信。而且原文中的时间相差并不大,不能说明什么问题,这只能说明lambda初值的设置对于收敛速度是有影响的。
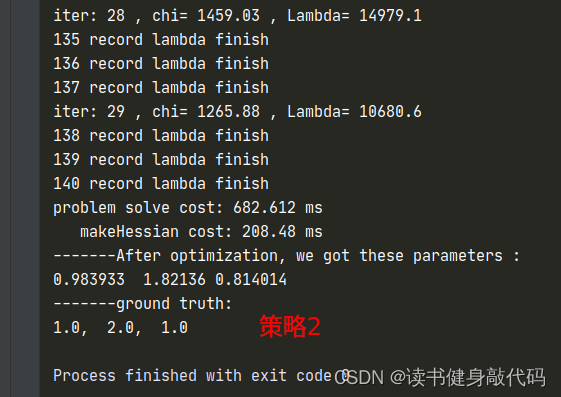
1.3.2 策略2
λ
,
Δ
x
,
ρ
\lambda, \Delta x,\rho
λ,Δx,ρ计算同初值设置同策略3
只是计算cost时需要考虑
Δ
x
\Delta x
Δx的系数,需要重新计算临时的cost,在满足更新x的条件之后在更新
α
\alpha
α和
x
x
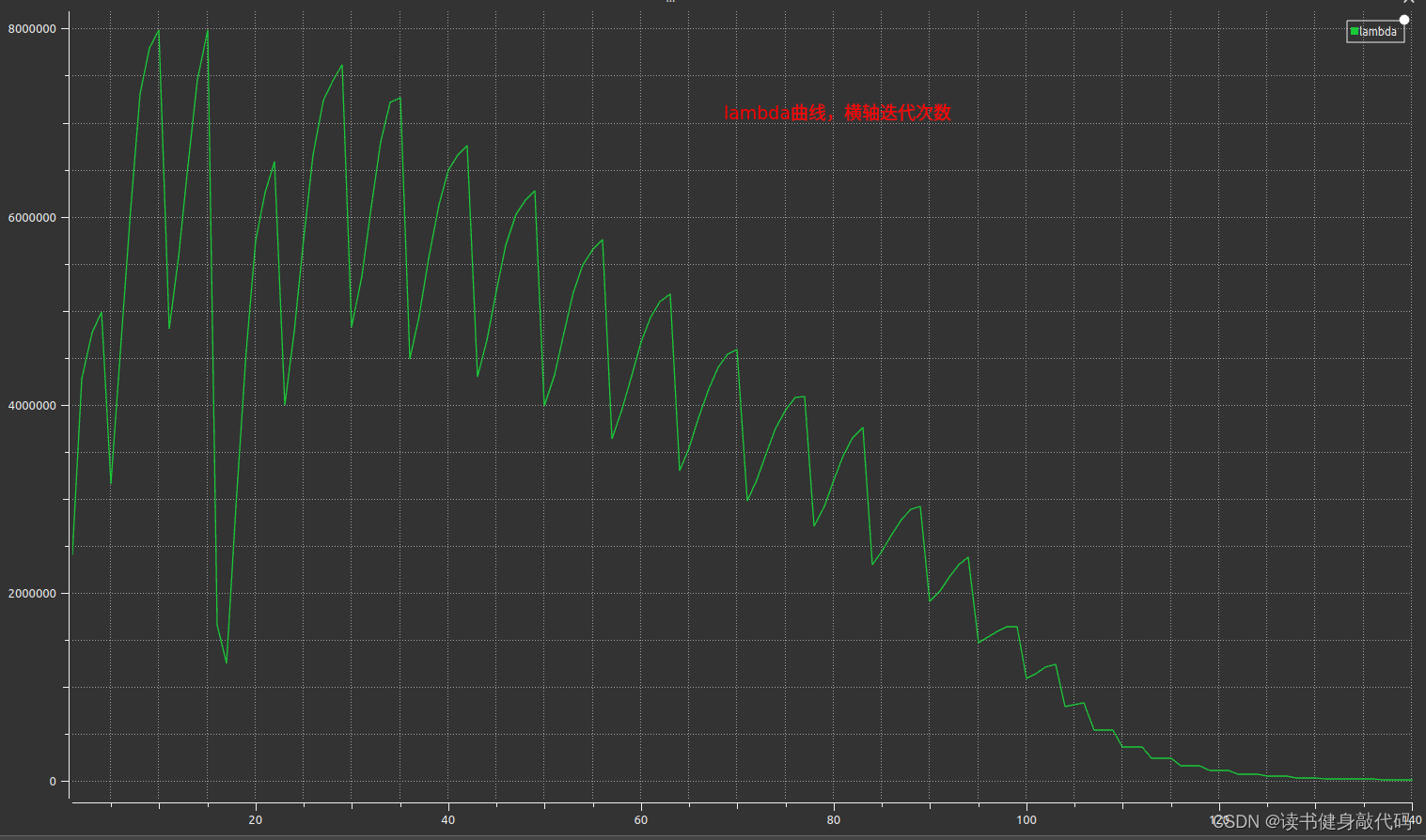
x,自己实现了一版,但是这个运行时间让我感觉是有些问题的,放上代码和
λ
\lambda
λ的曲线,如果有大佬实现出来了告诉我一下~:
整个problem.cc文件
#include <iostream>
#include <fstream>
#include <eigen3/Eigen/Dense>
#include <glog/logging.h>
#include "backend/problem.h"
#include "utils/tic_toc.h"
#ifdef USE_OPENMP
#include <omp.h>
#endif
using namespace std;
//problem edge等构造函数后面第6讲会再讲,现在只先熟悉即可。
namespace myslam {
namespace backend {
void Problem::LogoutVectorSize() {
// LOG(INFO) <<
// "1 problem::LogoutVectorSize verticies_:" << verticies_.size() <<
// " edges:" << edges_.size();
}
Problem::Problem(ProblemType problemType) :
problemType_(problemType) {
LogoutVectorSize();
verticies_marg_.clear();
}
Problem::~Problem() {}
bool Problem::AddVertex(std::shared_ptr<Vertex> vertex) {
if (verticies_.find(vertex->Id()) != verticies_.end()) {
// LOG(WARNING) << "Vertex " << vertex->Id() << " has been added before";
return false;
} else {
verticies_.insert(pair<unsigned long, shared_ptr<Vertex>>(vertex->Id(), vertex));
}
return true;
}
bool Problem::AddEdge(shared_ptr<Edge> edge) {
if (edges_.find(edge->Id()) == edges_.end()) {
edges_.insert(pair<ulong, std::shared_ptr<Edge>>(edge->Id(), edge));
} else {
// LOG(WARNING) << "Edge " << edge->Id() << " has been added before!";
return false;
}
for (auto &vertex: edge->Verticies()) {
vertexToEdge_.insert(pair<ulong, shared_ptr<Edge>>(vertex->Id(), edge));//由vertex id查询edge
}
return true;
}
bool Problem::Solve(int iterations) {
if (edges_.size() == 0 || verticies_.size() == 0) {
std::cerr << "\nCannot solve problem without edges or verticies" << std::endl;
return false;
}
TicToc t_solve;
// 统计优化变量的维数,为构建 H 矩阵做准备
SetOrdering();
// 遍历edge, 构建 H = J^T * J 矩阵
MakeHessian();
// LM 初始化
ComputeLambdaInitLM();
// LM 算法迭代求解
bool stop = false;
int iter = 0;
//尝试的lambda次数
try_iter_ = 0;
//保存LM阻尼阻尼系数lambda
file_name_ = "./lambda.csv";
FILE *tmp_fp = fopen(file_name_.data(), "w");
fprintf(tmp_fp, "iter, lambda\n");
fflush(tmp_fp);
fclose(tmp_fp);
while (!stop && (iter < iterations)) {
std::cout << "iter: " << iter << " , chi= " << currentChi_ << " , Lambda= " << currentLambda_
<< std::endl;
bool oneStepSuccess = false;
int false_cnt = 0;
while (!oneStepSuccess) // 不断尝试 Lambda, 直到成功迭代一步
{
++try_iter_;
// setLambda
AddLambdatoHessianLM();
// 第四步,解线性方程 H X = B
SolveLinearSystem();
//
RemoveLambdaHessianLM();
// 优化退出条件1: delta_x_ 很小则退出
if (delta_x_.squaredNorm() <= 1e-6 || false_cnt > 10) {
stop = true;
printf("delta_x too small: %f, or false_cnt=%d > 10 break\n", delta_x_.squaredNorm(), false_cnt);
break;
}
// 更新状态量 X = X+ delta_x
UpdateStates();
// 判断当前步是否可行以及 LM 的 lambda 怎么更新
oneStepSuccess = IsGoodStepInLM();//误差是否下降
// 后续处理,
if (oneStepSuccess) {
// 在新线性化点 构建 hessian
alpha_ = alpha_tmp_;
MakeHessian();
// TODO:: 这个判断条件可以丢掉,条件 b_max <= 1e-12 很难达到,这里的阈值条件不应该用绝对值,而是相对值
// double b_max = 0.0;
// for (int i = 0; i < b_.size(); ++i) {
// b_max = max(fabs(b_(i)), b_max);
// }
// // 优化退出条件2: 如果残差 b_max 已经很小了,那就退出
// stop = (b_max <= 1e-12);
false_cnt = 0;
} else {
false_cnt++;
RollbackStates(); // 误差没下降,回滚
}
}
iter++;
// 优化退出条件3: currentChi_ 跟第一次的chi2相比,下降了 1e6 倍则退出
if (sqrt(currentChi_) <= stopThresholdLM_) {
printf("currentChi_ decrease matched break condition");
stop = true;
}
}
std::cout << "problem solve cost: " << t_solve.toc() << " ms" << std::endl;
std::cout << " makeHessian cost: " << t_hessian_cost_ << " ms" << std::endl;
return true;
}
void Problem::SetOrdering() {
// 每次重新计数
ordering_poses_ = 0;
ordering_generic_ = 0;
ordering_landmarks_ = 0;
// Note:: verticies_ 是 map 类型的, 顺序是按照 id 号排序的
// 统计带估计的所有变量的总维度
for (auto vertex: verticies_) {
ordering_generic_ += vertex.second->LocalDimension(); // 所有的优化变量总维数
}
}
//可以暂时不看,后面会再讲
void Problem::MakeHessian() {
TicToc t_h;
// 直接构造大的 H 矩阵
ulong size = ordering_generic_;
MatXX H(MatXX::Zero(size, size));
VecX b(VecX::Zero(size));
// TODO:: accelate, accelate, accelate
//#ifdef USE_OPENMP
//#pragma omp parallel for
//#endif
// 遍历每个残差,并计算他们的雅克比,得到最后的 H = J^T * J
for (auto &edge: edges_) {
edge.second->ComputeResidual();
edge.second->ComputeJacobians();
auto jacobians = edge.second->Jacobians();
auto verticies = edge.second->Verticies();
assert(jacobians.size() == verticies.size());
for (size_t i = 0; i < verticies.size(); ++i) {
auto v_i = verticies[i];
if (v_i->IsFixed()) continue; // Hessian 里不需要添加它的信息,也就是它的雅克比为 0
auto jacobian_i = jacobians[i];
ulong index_i = v_i->OrderingId();
ulong dim_i = v_i->LocalDimension();
MatXX JtW = jacobian_i.transpose() * edge.second->Information();
for (size_t j = i; j < verticies.size(); ++j) {
auto v_j = verticies[j];
if (v_j->IsFixed()) continue;
auto jacobian_j = jacobians[j];
ulong index_j = v_j->OrderingId();
ulong dim_j = v_j->LocalDimension();
assert(v_j->OrderingId() != -1);
MatXX hessian = JtW * jacobian_j;
// 所有的信息矩阵叠加起来
H.block(index_i, index_j, dim_i, dim_j).noalias() += hessian;
if (j != i) {
// 对称的下三角
H.block(index_j, index_i, dim_j, dim_i).noalias() += hessian.transpose();
}
}
b.segment(index_i, dim_i).noalias() -= JtW * edge.second->Residual();
}
}
Hessian_ = H;
b_ = b;
t_hessian_cost_ += t_h.toc();
delta_x_ = VecX::Zero(size); // initial delta_x = 0_n;
}
/*
* Solve Hx = b, we can use PCG iterative method or use sparse Cholesky
*/
void Problem::SolveLinearSystem() {
delta_x_ = Hessian_.inverse() * b_;
// delta_x_ = H.ldlt().solve(b_);
}
void Problem::UpdateStates() {
for (auto vertex: verticies_) {
ulong idx = vertex.second->OrderingId();
ulong dim = vertex.second->LocalDimension();
VecX delta = delta_x_.segment(idx, dim);
// 所有的参数 x 叠加一个增量 x_{k+1} = x_{k} + delta_x
vertex.second->Plus( alpha_ * delta);
}
}
void Problem::RollbackStates() {
for (auto vertex: verticies_) {
ulong idx = vertex.second->OrderingId();
ulong dim = vertex.second->LocalDimension();
VecX delta = delta_x_.segment(idx, dim);
// 之前的增量加了后使得损失函数增加了,我们应该不要这次迭代结果,所以把之前加上的量减去。
vertex.second->Plus(alpha_ * (-delta));
}
}
/// LM
void Problem::ComputeLambdaInitLM() {
ni_ = 2.;
// currentLambda_ = -1.;
currentChi_ = 0.0;
// TODO:: robust cost chi2
for (auto edge: edges_) {
currentChi_ += edge.second->Chi2();
}
if (err_prior_.rows() > 0)
currentChi_ += err_prior_.norm();
stopThresholdLM_ = 1e-6 * currentChi_; // 迭代条件为 误差下降 1e-6 倍
double maxDiagonal = 0;
ulong size = Hessian_.cols();
assert(Hessian_.rows() == Hessian_.cols() && "Hessian is not square");
for (ulong i = 0; i < size; ++i) {
maxDiagonal = std::max(fabs(Hessian_(i, i)), maxDiagonal);//取H矩阵的最大值,然后*涛
}
double tau = 1e-5;
currentLambda_ = tau * maxDiagonal;
// currentLambda_ = 1e-3;
// currentLambda_ = 1e3;
// set a large value, so that first updates are small steps in the steepest-descent direction
}
//这个关于Hessian矩阵的我还搞不懂
void Problem::AddLambdatoHessianLM() {
ulong size = Hessian_.cols();
assert(Hessian_.rows() == Hessian_.cols() && "Hessian is not square");
for (ulong i = 0; i < size; ++i) {
Hessian_(i, i) += currentLambda_; //策略2,3
// Hessian_(i, i) += currentLambda_ * Hessian_(i, i); //理解: H(k+1) = H(k) + λ H(k) = (1+λ) H(k) 策略1
}
}
void Problem::RemoveLambdaHessianLM() {
ulong size = Hessian_.cols();
assert(Hessian_.rows() == Hessian_.cols() && "Hessian is not square");
// TODO:: 这里不应该减去一个,数值的反复加减容易造成数值精度出问题?而应该保存叠加lambda前的值,在这里直接赋值
for (ulong i = 0; i < size; ++i) {
Hessian_(i, i) -= currentLambda_; //策略2,3
// Hessian_(i, i) /= 1.0 + currentLambda_;//H回退: H(k) = 1/(1+λ) * H(k+1),策略1
}
}
//Nielsen的方法,分母直接为L,判断\rho的符号
bool Problem::IsGoodStepInLM() {
bool ret = false;
/*策略2更新策略*/
// double scale = 0;
// scale = delta_x_.transpose() * (currentLambda_ * delta_x_ + b_);
// scale += 1e-3; // make sure it's non-zero :)
// recompute residuals after update state
// 统计所有的残差
double tempChi_p_h = 0.0, tempChi_p_alpha_h = 0.0;
for (auto edge: edges_) {
edge.second->ComputeResidual();
tempChi_p_h += edge.second->Chi2();//计算cost
}
double alpha_up = b_.transpose() * delta_x_;
double alpha_down = (tempChi_p_h - currentChi_) / 2. + 2. * alpha_up;
alpha_tmp_ = alpha_up / alpha_down;
double scale = 0;
scale = alpha_tmp_ * delta_x_.transpose() * (currentLambda_ * alpha_tmp_ * delta_x_ + b_);
scale += 1e-3; // make sure it's non-zero :)
HashEdge tmp_edges = edges_;
HashVertex tmp_vertecies = verticies_;
//更新x以计算新的cost
for (auto vertex: tmp_vertecies) {
ulong idx = vertex.second->OrderingId();
ulong dim = vertex.second->LocalDimension();
VecX delta = delta_x_.segment(idx, dim);
// 所有的参数 x 叠加一个增量 x_{k+1} = x_{k} + delta_x
vertex.second->Plus(alpha_tmp_ * delta);
}
for (auto edge: tmp_edges) {
edge.second->ComputeResidual();
tempChi_p_alpha_h += edge.second->Chi2();//计算cost
}
double rho_alpha_h = (tempChi_p_alpha_h - currentChi_) / scale; //tempChi的计算中的alpha*delta_x已经在x = x + alpha*delta_x更新的时候算上了
if (rho_alpha_h > 0 && isfinite(tempChi_p_alpha_h)) { // last step was good, 误差在下降
currentLambda_ = std::max(currentLambda_ / (1 + alpha_tmp_), 1e-7);
currentChi_ = tempChi_p_h; //这里应该是用现在的,而不是临时更新出来的,在外面更新
ret = true;
} else {
currentLambda_ = currentLambda_ + fabs(tempChi_p_alpha_h - currentChi_) / (2 * alpha_tmp_);
ret = false;
}
/*策略2更新策略*/
FILE *fp_lambda = fopen(file_name_.data(), "a");
fprintf(fp_lambda, "%d, %f\n", try_iter_, currentLambda_);
fflush(fp_lambda);
fclose(fp_lambda);
printf("%d record lambda finish\n", try_iter_);
return ret;
}
/** @brief conjugate gradient with perconditioning
*
* the jacobi PCG method
*
*/
VecX Problem::PCGSolver(const MatXX &A, const VecX &b, int maxIter = -1) {
assert(A.rows() == A.cols() && "PCG solver ERROR: A is not a square matrix");
int rows = b.rows();
int n = maxIter < 0 ? rows : maxIter;
VecX x(VecX::Zero(rows));
MatXX M_inv = A.diagonal().asDiagonal().inverse();
VecX r0(b); // initial r = b - A*0 = b
VecX z0 = M_inv * r0;
VecX p(z0);
VecX w = A * p;
double r0z0 = r0.dot(z0);
double alpha = r0z0 / p.dot(w);
VecX r1 = r0 - alpha * w;
int i = 0;
double threshold = 1e-6 * r0.norm();
while (r1.norm() > threshold && i < n) {
i++;
VecX z1 = M_inv * r1;
double r1z1 = r1.dot(z1);
double belta = r1z1 / r0z0;
z0 = z1;
r0z0 = r1z1;
r0 = r1;
p = belta * p + z1;
w = A * p;
alpha = r1z1 / p.dot(w);
x += alpha * p;
r1 -= alpha * w;
}
return x;
}
}
}
2. 推导公式
2.2 f 15 f_{15} f15
同样地,
α
b
i
b
k
+
1
\alpha_{b_ib_{k+1}}
αbibk+1将a带入之后也只与下图的红色部分有关

于是剩下的为:(其实不明白为什么最后有的项还会有
ω
\omega
ω)
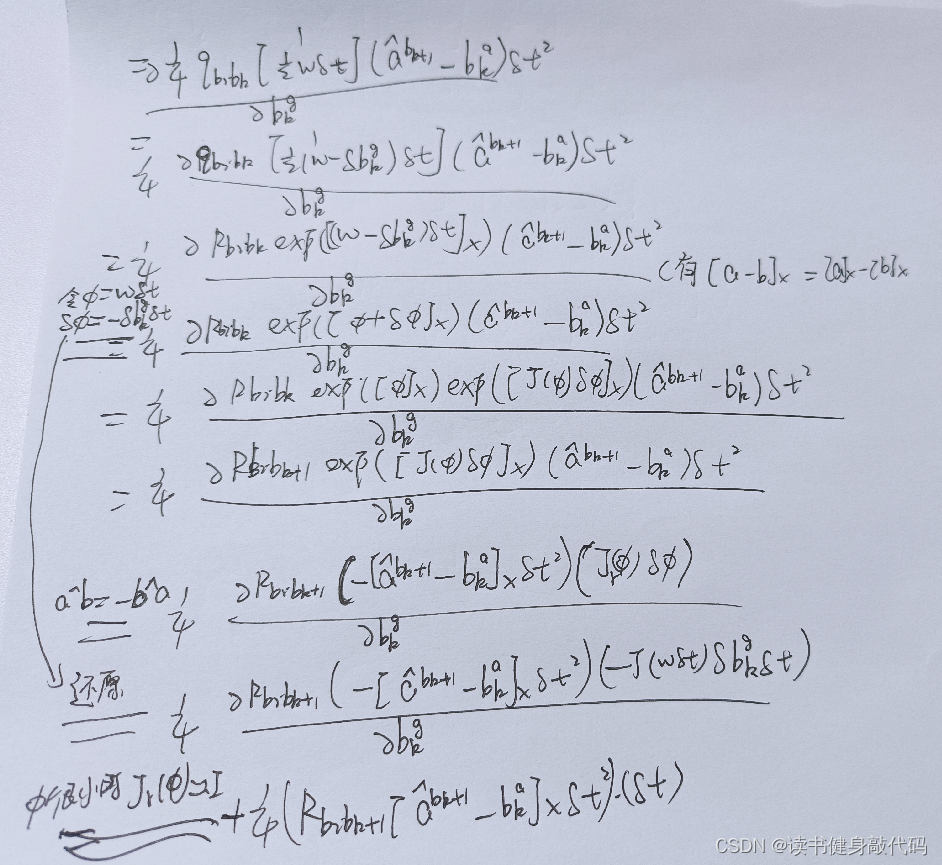
其中令
ϕ
=
ω
δ
t
,
δ
ϕ
=
−
δ
b
k
g
δ
t
\phi=\omega\delta t,\delta\phi=-\delta b_k^g\delta t
ϕ=ωδt,δϕ=−δbkgδt很关键,并用了下述公式:

2.2 g 12 g_{12} g12

所以刚才的疑问,为什么有的会有 ω \omega ω,那是在那一项将 ω \omega ω展开之后也跟被导量无关的时候才会不展开 ω \omega ω,比如 f 22 f_{22} f22中, ω \omega ω的展开量对角度 θ \theta θ是无关的,所以可以保留 ω \omega ω。
2.3 推导总结
针对被导量,将分母展开,取与被导量有关的项进行求导,无关的都扔掉,比如大多数导数都对 n k g , n k a n_k^g,n_k^a nkg,nka无关,所以有时候干脆不写,直接扔掉了,但是像2.2节中的与n_k^g有关,所以就反而只与 n k g n_k^g nkg有关,把握这个原则就能推出其它。
3. T3
式(9)来源:
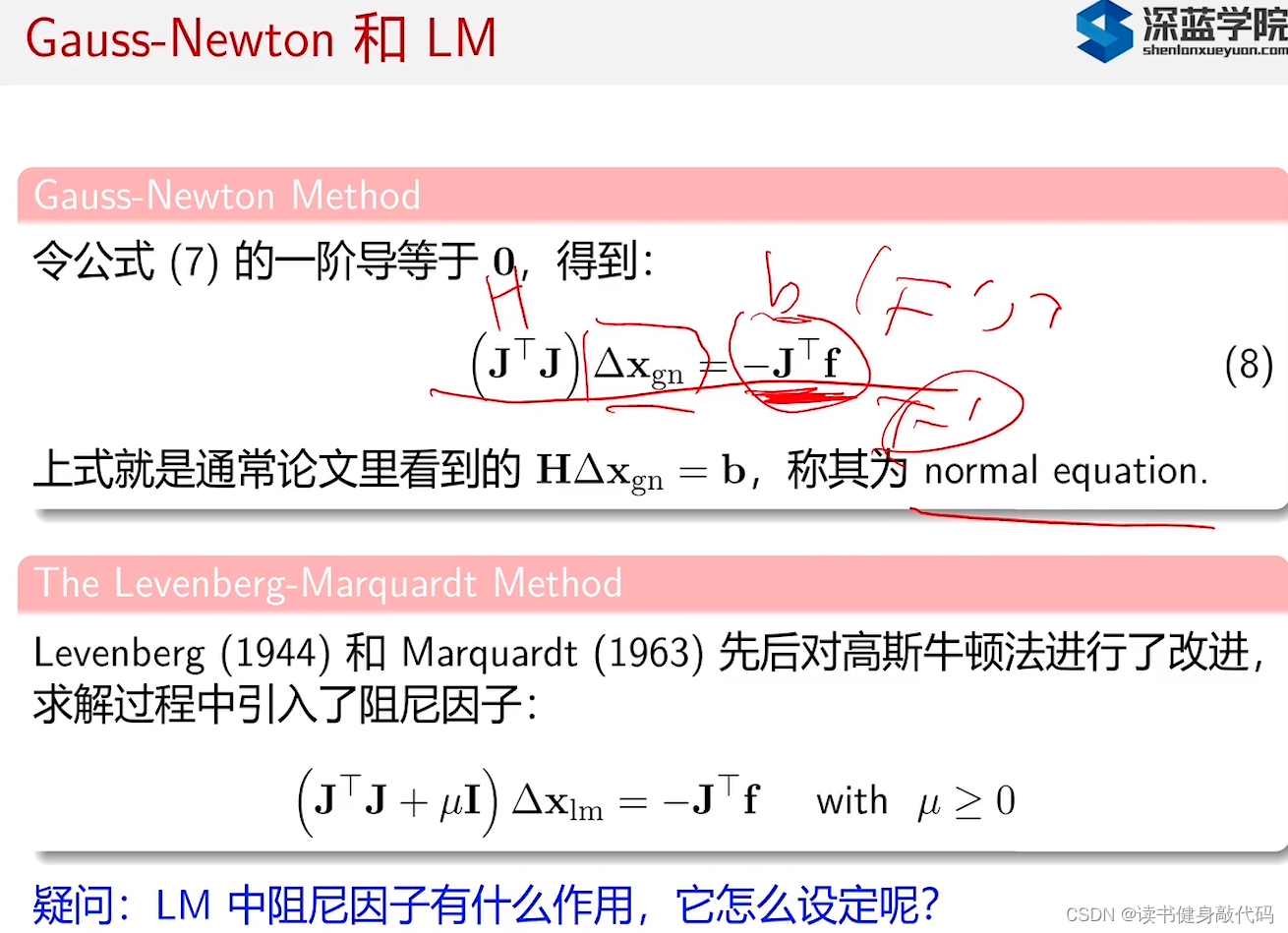

图片来自(不想去水印了):博客
数学基础太差,有些看不懂怎么把前面系数项移到右边的。

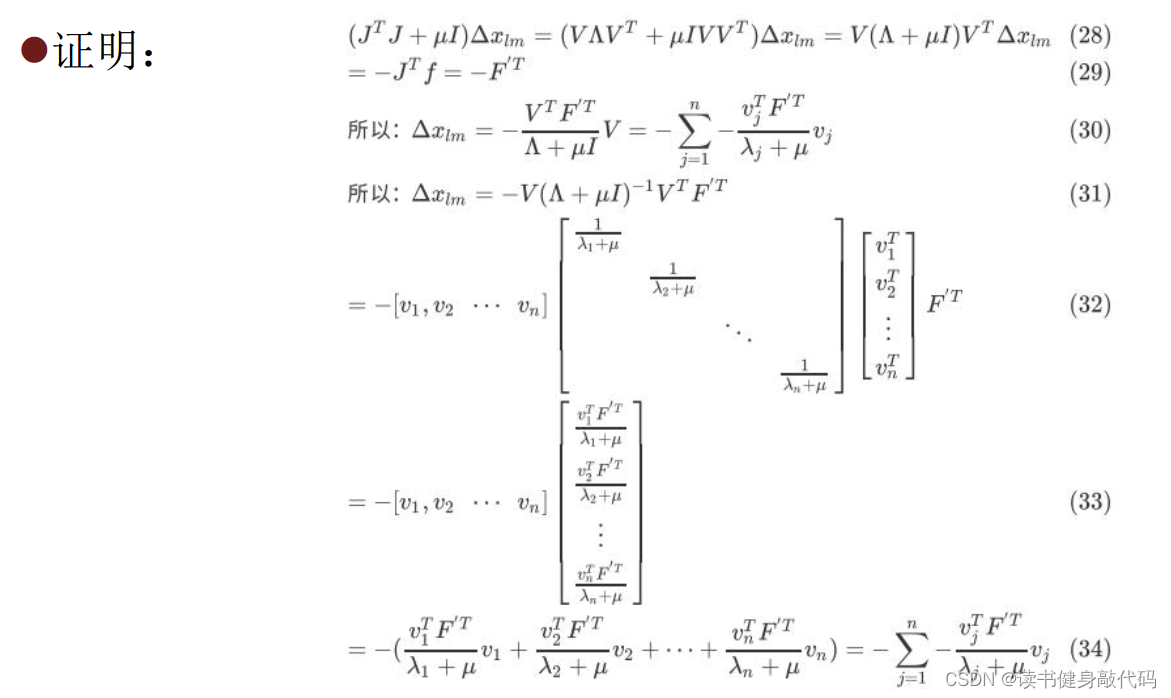
助教给的答案也看不太懂:
本章完。






(Matlab代码实现)](https://img-blog.csdnimg.cn/d478c2c49d894ac3b9740b19a7e998ac.png)


![[论文阅读] (31)李沐老师视频学习——4.研究的艺术·理由、论据和担保](https://img-blog.csdnimg.cn/4d4a9a2edc814a68bfb40eac06927424.png#pic_center)