一 基本概念
SBT(Size Balanced Tree,节点大小平衡树)是一种自平衡二叉查找树,通过子树的大小来保持平衡。与红黑树、AVL 树等自平衡二叉查找树相比,SBT更易于实现。SBT 可以在 O (logn) 时间内完成所有二叉搜索树的相关操作,与普通二叉搜索树相比,SBT 仅加入了简洁的核心操作 maintain。由于 SBT 保持平衡的是size 域而不是其他“无用”的域,所以可以方便地实现动态顺序统计中的第 k 小和排名操作。
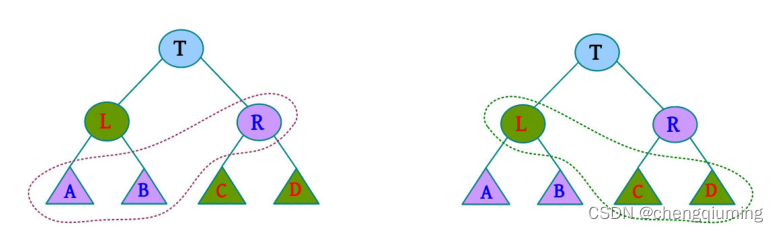
对 SBT 的每个节点 T,节点 L 和 R 分别是节点 T 的左右儿子,子树 A、B、C 和 D 分别是节点 L 和 R 的左右子树。T 右子树的大小都大于或等于 T 左子树两个子节点的大小,size[R]≥size[A],size[R]≥size[B];T 左子树的大小都大于或等于 T 右子树两个子节点的大小,size[L] ≥ size[C],size[L] ≥ size[D]。也就是说,“叔叔”≥“侄子”。
二 基础操作
1 右旋和左旋
SBT 的旋转也是以右旋和左旋为基础的,旋转也是 maintain 操作的基础。
(1)右旋。
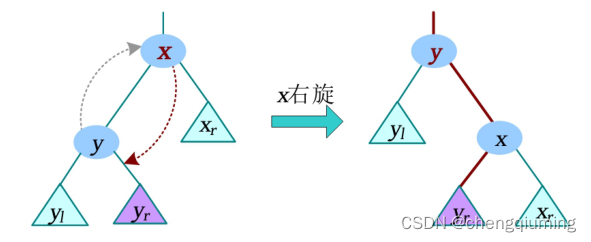
x 右旋时,携带自己的右子节点向右旋转到 y 的右子树位置,y 的右子树被抛弃,x 右旋后左子树正好空闲,将 y 的右子树放在 x 的左子树上。更新 y 子树的大小等于 x 子树的大小,x 子树
的大小为其左右子树大小之和加 1。
(2)左旋。
x 左旋时,携带自己的左子节点向左旋转到 y 的左子树位置,y 的左子树被抛弃,x 左旋后右子树正好空闲,将 y 的左子树放在 x 的右子树上。更新 y 子树的大小等于 x 子树的大小,x 子树
的大小为其左右子树大小之和加 1。
2 维护
(1)LL型
一棵 SBT,若将新节点 x 插入节点 A(T 左子树的左子树)之后,节点 T 出现了不平衡(size[A]>size[R],即“侄子”大于“叔叔”),则该树属于 LL 型不平衡,需要将节点 T 右旋。
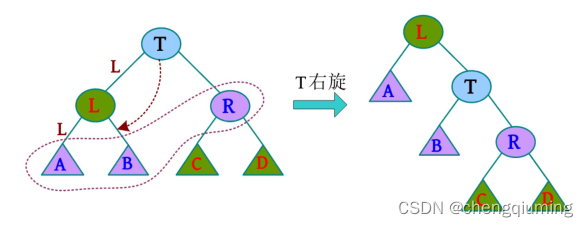
旋转之后 , A 、 B 和 R 仍 是 SBT 。 L 的右子树T可能会出现 size[C] > size[B] 或 size[D] > size[B] 的情况,即 RL、RR 型不平衡。因为 size[B] ≤ size[R],所以不会出现 B 的子树比 R 大的情况,即 T 不会出
现 LR、LL 型不平衡。因此 L 的右子树只需向右判断两种不平衡 RL、RR 即可。旋转后,L 自身也可能出现不平衡,需要继续调整平衡。
(2)LR型
有一棵 SBT,若新节点 x 插入节点B(T 左子树的右子树)之后,节点 T 出现了不平衡(size[B]>size[R]),则属于 LR 型不平衡,需要先将节点 L 左旋,然后将节点 T 右旋。
两次旋转之后,A、E、F 和 R 仍是 SBT。B 的右子树 T可能会出现 size[C]>size[F] 或 size[D]>size[F],即 RL、RR 型不平衡。因为在插
入节点之前 , size[B]≤size[R] , 插入新节点之后 ,size[B] > size[R] 。 实际上 , size[B] 最多比 size[R] 大 1 ,size[B]=size[E]+size[F]+1=size[R]+1,因此 size[F] ≤ size[R],不会出现 F 的子树比 R 大的情况,即T 不会出现 LR、LL 型不平衡。因此 B 的右子树只需向右判断两种不平衡 RL、RR 即可。
B 的左子树 L,size[E] ≤ size[A],因此 B 的左子树只需向左判断两种不平衡 LR、LL 即可。旋转后 B 自身都有可能出现不平衡,需要继续调整平衡。
总结:旋转之后,树根的左子树只需向左判断调整平衡,树根的右子树只需向右判断调整平衡,树根需要在两个方向判断调整平衡。
(3)RR型
该类型与 LL 型对称。
(4)RL型
该类型与 LR 型对称。
三 基本操作
SBT 的 9 种基本操作:插入、删除、查找、最小值/最大值、前驱/后继、排名、第k 小。
(1)插入
从树根开始,若当前节点为空,则创建一个新节点,否则当前节点的大小加1。若待插入元素 val 小于当前节点的值,则插入当前节点的左子树,否则插入当前节点的右子树,然后根据插入子树的不同进行维护。
(2)删除
删除操作和二叉搜索树的删除方法相同。删除节点之后,虽然不能保证这棵树是 SBT,但是整棵树的最大深度并没有变化,所以时间复杂度不会增加。这时,maintain 操作显得多余,因此删除操作没有调整平衡。
(3)查找
查找操作和二叉搜索树的查找方法一样,从树根开始,若当前节点为空或待查找元素 val 等于当前节点的值,则返回当前节点;若 val 小于当前节点的值,则到当前节点的左子树中查找,否则到当前节点的右子树中查找。
(4)最小值
SBT 是一棵二叉搜索树,满足中序有序性,因此从根开始一直向左,找到的最左节点就是最小节点。
(5)最大值
根据 SBT 的中序有序性,从根开始找到的最右节点就是最大节点。
(6)前驱
求 val 的前驱,从根开始,用 p 记录当前节点,用 q 记录查找路径上的前一个节点。若 val 大于当前节点的值,则到右子树中搜索,否则到左子树中搜索,当 p 为空时返回的 q 节点的值,即为 val 的前驱。
(7)后继
求 val 的后继,从根开始,p 记录当前节点,q 记录查找路径上的前一个节点。若 val 小于当前节点的值,则到左子树中搜索,否则到右子树中搜索,当 p 为空时返回的 q 节点的值,即为 val 的后继。
(8)排名
求 val 的排名,从根开始,若 val 小于当前节点的值,则返回在左子树中的排名;若 val 大于当前节点的值,则返回在右子树中的排名+左子树的大小+1;若 va l等于当前节点的值,则返回左子树的大小+1。
(9)第 k 小。、
从根开始,用 s 记录左子树的大小+1,若 s 等于 k,则返回当前节点的值;若s 小于 k ,则到右子树中查找第 k -s 个节点,否则到左子树中查找第 k 个节点。
四 代码
package com.platform.modules.alg.alglib.p434;
public class P434 {
public String output = "";
private int maxn = 100005;
int n, cnt; // 结点数,结点存储下标累计
node tr[] = new node[maxn];
public P434() {
for (int i = 0; i < tr.length; i++) {
tr[i] = new node();
}
}
// 树根
nodePtr root = new nodePtr();
public String cal(String input) {
cnt = 0;
int n, x;
int count = 0;
while (true) {
String[] line = input.split("\n");
String[] command = line[count++].split(" ");
n = Integer.parseInt(command[0]);
switch (n) {
case 0:
return output;
case 1: // 插入
x = Integer.parseInt(command[1]);
insert(root, x);
break;
case 2: // 删除
x = Integer.parseInt(command[1]);
remove(root, x);
break;
case 3: // 查找
x = Integer.parseInt(command[1]);
if (find_v(root.ptr, x) > 0)
output += "find success!\n";
else
output += "find fail!\n";
break;
case 4: // 最小值
output += get_min() + "\n";
break;
case 5: // 最大值
output += get_max() + "\n";
break;
case 6: // 前驱
x = Integer.parseInt(command[1]);
output += get_pre(root, 0, x) + "\n";
break;
case 7: // 后继
x = Integer.parseInt(command[1]);
output += get_next(root, 0, x) + "\n";
break;
case 8: // 排名
x = Integer.parseInt(command[1]);
output += get_rank(root, x) + "\n";
break;
case 9: // 第K小
x = Integer.parseInt(command[1]);
output += get_kth(root, x) + "\n";
break;
case 10: // 输出
in_order(root.ptr);
break;
}
}
}
void R_rotate(nodePtr x) {
int y = tr[x.ptr].lc.ptr;
tr[x.ptr].lc.ptr = tr[y].rc.ptr;
tr[y].rc.ptr = x.ptr;
tr[y].size = tr[x.ptr].size;
tr[x.ptr].size = tr[tr[x.ptr].lc.ptr].size + tr[tr[x.ptr].rc.ptr].size + 1;
x.ptr = y;
}
void L_rotate(nodePtr x) {
int y = tr[x.ptr].rc.ptr;
tr[x.ptr].rc.ptr = tr[y].lc.ptr;
tr[y].lc.ptr = x.ptr;
tr[y].size = tr[x.ptr].size;
tr[x.ptr].size = tr[tr[x.ptr].lc.ptr].size + tr[tr[x.ptr].rc.ptr].size + 1;
x.ptr = y;
}
void maintain(nodePtr p, boolean flag) {
if (p.ptr == 0) return;
if (!flag) {
if (tr[tr[tr[p.ptr].lc.ptr].lc.ptr].size > tr[tr[p.ptr].rc.ptr].size) // LL
R_rotate(p);
else if (tr[tr[tr[p.ptr].lc.ptr].rc.ptr].size > tr[tr[p.ptr].rc.ptr].size) { // LR
L_rotate(tr[p.ptr].lc);
R_rotate(p);
} else return;
} else {
if (tr[tr[tr[p.ptr].rc.ptr].rc.ptr].size > tr[tr[p.ptr].lc.ptr].size)//RR
L_rotate(p);
else if (tr[tr[tr[p.ptr].rc.ptr].lc.ptr].size > tr[tr[p.ptr].lc.ptr].size) {//RL
R_rotate(tr[p.ptr].rc);
L_rotate(p);
} else return;
}
maintain(tr[p.ptr].lc, false);
maintain(tr[p.ptr].rc, true);
maintain(p, false);
maintain(p, true);
}
void insert(nodePtr p, int val) {
if (p.ptr == 0) {
p.ptr = ++cnt;
tr[p.ptr].lc.ptr = tr[p.ptr].rc.ptr = 0;
tr[p.ptr].size = 1;
tr[p.ptr].val = val;
} else {
tr[p.ptr].size++;
if (val < tr[p.ptr].val) insert(tr[p.ptr].lc, val);
else insert(tr[p.ptr].rc, val);
maintain(p, val >= tr[p.ptr].val);
}
}
int find_v(int p, int val) {
if (p == 0 || tr[p].val == val) return p;
if (val < tr[p].val) return find_v(tr[p].lc.ptr, val);
else return find_v(tr[p].rc.ptr, val);
}
void remove(nodePtr p, int val) {
if (p.ptr == 0) return;
tr[p.ptr].size--;
if (tr[p.ptr].val == val) {
if (tr[p.ptr].lc.ptr == 0 || tr[p.ptr].rc.ptr == 0)
p.ptr = tr[p.ptr].lc.ptr + tr[p.ptr].rc.ptr; // 有一个儿子为空,直接用儿子代替
else { // 找后继,右子树最左节点
int temp = tr[p.ptr].rc.ptr;
while (tr[temp].lc.ptr > 0)
temp = tr[temp].lc.ptr;
tr[p.ptr].val = tr[temp].val;
remove(tr[p.ptr].rc, tr[temp].val);
}
} else if (val < tr[p.ptr].val) remove(tr[p.ptr].lc, val);
else remove(tr[p.ptr].rc, val);
}
int get_min() {
int p = root.ptr;
while (tr[p].lc.ptr > 0) p = tr[p].lc.ptr;
return tr[p].val;
}
int get_max() {
int p = root.ptr;
while (tr[p].rc.ptr > 0) p = tr[p].rc.ptr;
return tr[p].val;
}
int get_pre(nodePtr p, int q, int val) { // 求val的前驱
if (p.ptr == 0) return tr[q].val;
if (tr[p.ptr].val < val)
return get_pre(tr[p.ptr].rc, p.ptr, val);
else return get_pre(tr[p.ptr].lc, q, val);
}
int get_next(nodePtr p, int q, int val) { // 求 val 的后继
if (p.ptr == 0) return tr[q].val;
if (tr[p.ptr].val > val)
return get_next(tr[p.ptr].lc, p.ptr, val);
else return get_next(tr[p.ptr].rc, q, val);
}
int get_rank(nodePtr p, int val) { // 求 val 的排名
if (val < tr[p.ptr].val)
return get_rank(tr[p.ptr].lc, val);
else if (val > tr[p.ptr].val)
return get_rank(tr[p.ptr].rc, val) + tr[tr[p.ptr].lc.ptr].size + 1;
return tr[tr[p.ptr].lc.ptr].size + 1;
}
int get_kth(nodePtr p, int k) { // 求第 k 小数,select
int s = tr[tr[p.ptr].lc.ptr].size + 1;
if (s == k) return tr[p.ptr].val;
else if (s < k) return get_kth(tr[p.ptr].rc, k - s);
else return get_kth(tr[p.ptr].lc, k);
}
void in_order(int p) {
if (p == 0) return;
in_order(tr[p].lc.ptr);
output += tr[p].val + " " + tr[p].size + " " + tr[tr[p].lc.ptr].val + " " + tr[tr[p].rc.ptr].val + " " + "\n";
in_order(tr[p].rc.ptr);
}
}
class node {
nodePtr lc = new nodePtr(); // 左孩子
nodePtr rc = new nodePtr(); // 右孩子
int val; // 值
int size; // 子树大小
}
class nodePtr {
int ptr;
}五 测试
1 输入
1 1
1 2
1 3
1 4
1 5
1 6
1 7
1 8
1 9
2 5
3 4
4
5
6 3
7 3
8 9
9 3
10
0
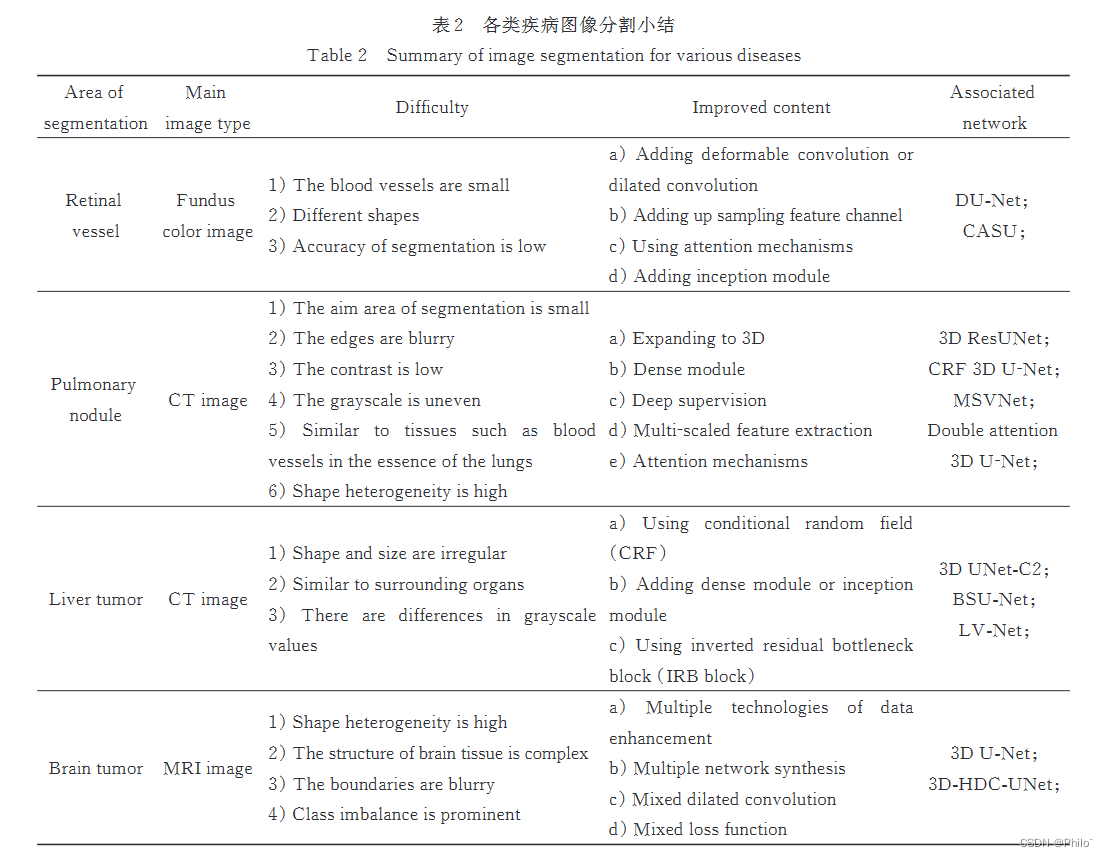
2 输出
find success!
1
9
2
4
8
3
1 1 0 0
2 3 1 3
3 1 0 0
4 8 2 6
6 4 0 8
7 1 0 0
8 3 7 9
9 1 0 0





![[附源码]计算机毕业设计基于Springboot校刊投稿系统](https://img-blog.csdnimg.cn/99bc9e9a7153402393ac294d5a099659.png)


![[附源码]计算机毕业设计实验室管理系统Springboot程序](https://img-blog.csdnimg.cn/ed1fcc114ea044ab8921e778407fe263.png)
![[附源码]计算机毕业设计三星小区车辆登记系统Springboot程序](https://img-blog.csdnimg.cn/38b4d629a2024d87afc268f1f26867d5.png)

![[附源码]计算机毕业设计JAVA婴幼儿玩具共享租售平台](https://img-blog.csdnimg.cn/3ce7887709cd4b13abb29cf13f8060cb.png)
