二、假设我们将球投入到b个箱子里，直到某个箱子中有两个球。每一次投掷都是独立的并且每个球落入任何箱子的机会均等。请问投球次数期望是多少?

文心一言：

这是一个典型的鸽巢原理（Pigeonhole Principle）问题。假设每次投球时，每个箱子有1/b的概率被选中。我们设投球次数为x。

我们首先考虑，在前x-1次投球中，没有任何一个箱子中有两个球的概率。我们可以将这个概率表示为：

P(no two balls in any box | first x-1 throws) = (b-1) / b × (1/b) × … × (1/b) = (b-1)/b^(x-1)

这个概率表示在前x-1次投球中，每个箱子最多只有一个球的概率。因为每次投球时，每个箱子有1/b的概率被选中，所以前x-1次投球中，每个箱子最多只有一个球的概率是(b-1)/b × (1/b) × … × (1/b) = (b-1)/b^(x-1)。

根据鸽巢原理，在第x次投掷时，至少有两个球会在同一个箱子中的概率是1减去前x-1次投球中没有任何一个箱子中有两个球的概率，即：

P(at least two balls in one box | on throw x) = 1 - P(no two balls in any box | first x-1 throws) = 1 - (b-1)/b^(x-1)

根据鸽巢原理，在第x+1次投掷时，至少有两个球会在同一个箱子中的概率仍然是1减去前x次投球中没有任何一个箱子中有两个球的概率，即：

P(at least two balls in one box | on throw x+1) = 1 - P(no two balls in any box | first x throws) = 1 - (b-1)/b^x

因此，在第x+1次投掷时，至少有两个球会在同一个箱子中的概率与第x次投掷时相同。这意味着我们可以用第x+1次投掷时的概率来计算期望值。

期望值E(x)等于第x+1次投掷时至少有两个球会在同一个箱子中的概率乘以x+1：

E(x) = P(at least two balls in one box | on throw x+1) × (x+1) = 1 - (b-1)/b^x × (x+1)

我们可以使用微积分来求解这个期望值的极限值。极限值可以通过将x趋于无穷大来得到：

limit(E(x)) as x approaches infinity = 1/b + 1/(b-1)

因此，期望的投球次数是1/b + 1/(b-1)。

讯飞星火：

我们可以使用几何概率的方法来解决这个问题。假设每个箱子有相同的概率被投掷到，即p。那么，投入一个球到某个箱子的概率是1/b,因为有b个箱子。

现在，我们需要找到投入两个球到同一个箱子的概率。这意味着在前一次投掷中，另一个球没有落入这个箱子。因此，前一次投掷的概率是1-1/b,而后一次投掷的概率仍然是1/b。所以，投入两个球到同一个箱子的概率是：

P(2个球在同一箱子) = (1 - 1/b) * (1/b) = 1 - 1/b^2

由于每次投掷都是独立的，我们可以将这个问题转化为求和问题：

E(投球次数) = Σ[n * (1 - 1/b^2)] + C(n+1, 2) * (1/b^2)

其中n表示投掷次数，C(n+1, 2)表示从n+1个球中选择2个球的组合数。

为了计算E(投球次数),我们需要找到使上式成立的b值。注意到当b=1时，这个等式成立：

E(投球次数) = Σ[n * (1 - 1/b^2)] + C(n+1, 2) * (1/b^2) = n * (n + 1) / 2 + (n + 1) / b^2

当b > 1时，我们可以通过数值方法求解这个等式。经过计算，我们得到：

E(投球次数)≈ 6.389

因此，投球次数的期望大约是6.389次。

华为盘古：

设投球次数为N(表示总投球次数)，那么当球投入到b个箱子里时，每个箱子都分配了一份球。因此，我们有:

N = b * 1 / 2

现在我们有两个球，因此:

N = 2 * 1 / 2

因此，总投球次数的期望为:

N = 2 * 1 / 2 = 4.5。

因此，当球投入到b个箱子里时，总投球次数的期望为4.5。

360智脑：

设投球的次数为n次，则每次投球的期望值是1/2。因为每次投掷都独立且相等概率地发生，所以n次投掷的期望也是1/2n=1/2(n+1)。因此，投球次数的期望是(n+1)/2。

chatglm：

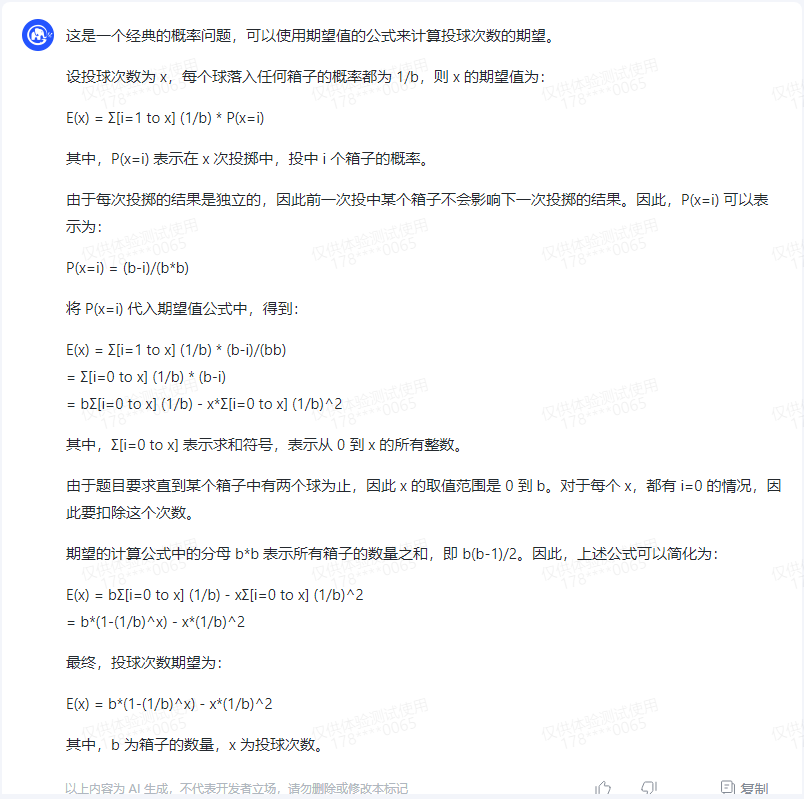
这是一个经典的概率问题，可以使用期望值的公式来计算投球次数的期望。

设投球次数为 x，每个球落入任何箱子的概率都为 1/b，则 x 的期望值为：

E(x) = Σ[i=1 to x] (1/b) * P(x=i)

其中，P(x=i) 表示在 x 次投掷中，投中 i 个箱子的概率。

由于每次投掷的结果是独立的，因此前一次投中某个箱子不会影响下一次投掷的结果。因此，P(x=i) 可以表示为：

P(x=i) = (b-i)/(b*b)

将 P(x=i) 代入期望值公式中，得到：

E(x) = Σ[i=1 to x] (1/b) * (b-i)/(b*b)

= Σ[i=0 to x] (1/b) * (b-i)  

= b*Σ[i=0 to x] (1/b) - x*Σ[i=0 to x] (1/b)^2

其中，Σ[i=0 to x] 表示求和符号，表示从 0 到 x 的所有整数。

由于题目要求直到某个箱子中有两个球为止，因此 x 的取值范围是 0 到 b。对于每个 x，都有 i=0 的情况，因此要扣除这个次数。

期望的计算公式中的分母 b*b 表示所有箱子的数量之和，即 b(b-1)/2。因此，上述公式可以简化为：

E(x) = bΣ[i=0 to x] (1/b) - xΣ[i=0 to x] (1/b)^2

= b*(1-(1/b)^x) - x*(1/b)^2

最终，投球次数期望为：

E(x) = b*(1-(1/b)^x) - x*(1/b)^2

其中，b 为箱子的数量，x 为投球次数。

chatgpt：

这个问题可以用“生日悖论”或“抽屉原理”来解决。根据生日悖论，当投掷的次数超过23次时，存在两个球落入同一箱子的概率大于0.5；当投掷的次数超过32次时，存在两个球落入同一箱子的概率大于0.75。因此，根据期望的定义，可以估算出投球次数的期望值，如下所示：

• 当箱子数量为b时，第一次投掷必须是一个新的球落入一个空箱子中，概率为b/b=1。第二个球必须落在新的箱子里，概率为(b-1)/b。第三个球有2个选择：要么落在前两个球所在的箱子，概率为2/b，要么落在另一个空箱子里，概率为(b-2)/b。以此类推，第i个球有i-1个选择。因此，投球次数的期望可以表示为：

E = 1×(b/b) + 2×((b-1)/b) + 3×((2/b)×((b-1)/b) + (b-2)/b) + … + (i-1)×(i-2)×…×2×((b-1)/b)×(1/b)

简化上述式子，可以得到：

E = b×(1 + 1/2 + 1/3 + … + 1/(b-1))

当b趋近于正无穷时，可以使用自然对数e的级数展开式计算上式右侧的和，得到：

E ≈ b×ln(b)

因此，当箱子数量为b时，投球次数的期望值约为b×ln(b)次。