文章目录
- 1前言
- 2 反射噪声去除RNR
- 3区域垂直平面拟合 (R-VPF)
- 4自适应地面似然估计(A-GLE)
- 5时序地面恢复TGR
- 总结
1前言
patchwork++是在patchwork的基础上进行改进的,主要有2个贡献:
- 提出了自适应地面似然估计(adaptive ground likelihood estimation (A-GLE)) 和时序地面恢复(temporal ground revert (TGR))
- 提出了两个新颖的异常值抑制模块,即反射噪声去除 (RNR) 和区域垂直平面拟合 (R-VPF)
相比于patchwork其工作流程图如下:
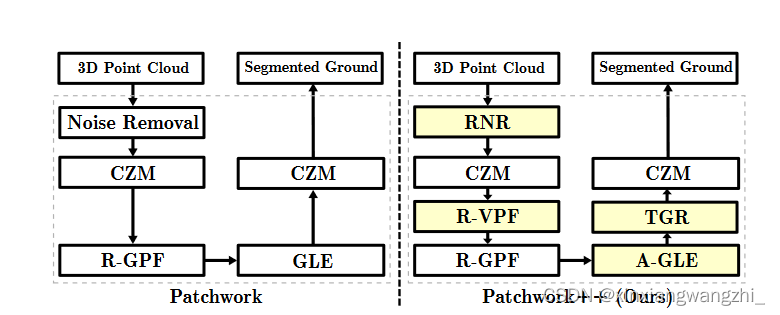
下面主要讨论patchwork的主要改进点:
2 反射噪声去除RNR
patchwork++假设bin的最低点为地面点,当地面以下有噪点,会把噪点误当为地面点。通常的做法是设置一个阈值,来去除地面以下的噪点,但是这种方法对于有坡度的地面是不适用的。
根据相关文献研究表明,地面以下的噪点具有以下两个特点:
首先,虚拟噪声点可以通过反射表面(即车辆的引擎盖和车顶或玻璃)上的反射而产生。如下图所示:当激光打到镜面时,入射角越小噪点位置越低。噪点是由于镜面反射的镜像点云造成的(或者说多路径效应)。所以,(当激光雷达高于反射镜面时)对于多线雷达,地面以下的噪点更可能是激光头下方的几线激光造成的。
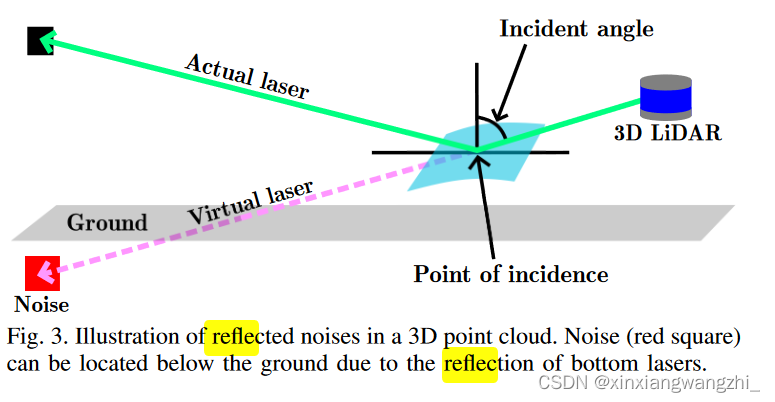
其次,地面以下的噪点通常具有低的强度,因为光线经过多次传播会减弱反射光线的强度。
因此,本文提出了一个地面以下的噪点去除方法,即去除激光头下方
N
n
o
i
s
e
N_{noise}
Nnoise个线束内,高度低于
h
n
o
i
s
e
h_{noise}
hnoise,并且强度低于
I
n
o
i
s
e
I_{noise}
Inoise的点云(并不是很高明的方法)。效果如下:
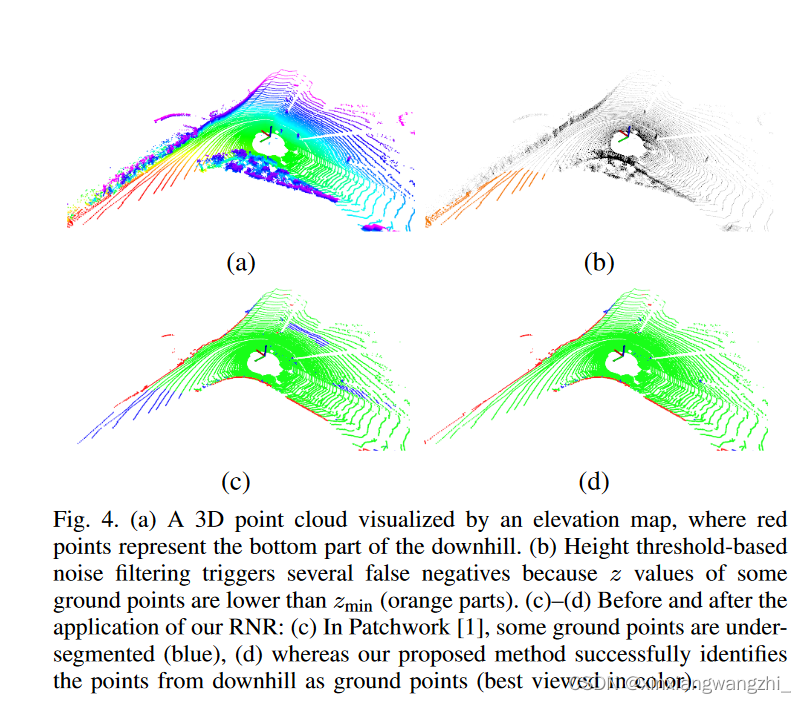
3区域垂直平面拟合 (R-VPF)
在之前的patchwork论文中使用的R-GPF对于垂直连接的地面的不适用。因为在水平和垂直地面连接处,只是用pca估计的法线会不准确。通过以下四个步骤确定垂直平面的点云
V
^
n
\hat{V}_{n}
V^n:第一步,在第k次迭代过程中选择最低点作为种子点。第二步,计算种子点的均值
m
n
k
m_{n}^{k}
mnk和单位法向量
v
3
k
v_{3}^{k}
v3k。然后潜在的垂直平面点云
W
^
n
k
\hat{W}_{n}^{k}
W^nk计算如下:
W
^
n
k
=
{
p
∈
P
^
n
k
∣
∣
(
p
−
m
n
k
)
⋅
v
3
,
n
k
∣
<
d
v
}
(2)
\hat{W}_{n}^{k}=\left\{\mathbf{p} \in \hat{P}_{n}^{k}||\left(\mathbf{p}-\mathbf{m}_{n}^{k}\right) \cdot \mathbf{v}_{3, n}^{k} \mid<d_{v}\right\}\tag{2}
W^nk={p∈P^nk∣∣(p−mnk)⋅v3,nk∣<dv}(2)
这种表达式的含义,即求点云与点云中心构成的向量与法线的相似度,
d
v
d_v
dv是阈值。
第三步,第k次迭代中垂直地面点
V
^
n
k
\hat{V}_{n}^{k}
V^nk计算如下:
V
^
n
k
=
{
W
^
n
k
,
if
π
2
−
cos
−
1
(
v
3
,
n
k
⋅
u
z
)
<
θ
v
∅
,
otherwise
\hat{V}_n^k= \begin{cases}\hat{W}_n^k, & \text { if } \frac{\pi}{2}-\cos ^{-1}\left(\mathbf{v}_{3, n}^k \cdot \mathbf{u}_z\right)<\theta_v \\ \varnothing, & \text { otherwise }\end{cases}
V^nk={W^nk,∅, if 2π−cos−1(v3,nk⋅uz)<θv otherwise
第四步,把之前所有k次迭代的结果相加得到所有的垂直点:
V
^
n
=
⋃
k
=
1
K
v
V
^
n
k
\hat{V}_n=\bigcup_{k=1}^{K_v} \hat{V}_n^k
V^n=k=1⋃KvV^nk
示意图如下:

4自适应地面似然估计(A-GLE)
在patchwork中GLE需要固定阈值,这里对高程阈值和平面度阈值进行改进:
- 高程:
e τ , m ← mean ( E m ) + a m ⋅ stdev ( E m ) e_{\tau, m} \leftarrow \operatorname{mean}\left(E_m\right)+a_m \cdot \operatorname{stdev}\left(E_m\right) eτ,m←mean(Em)+am⋅stdev(Em)
E m E_m Em是之前所有估计的 e n e_n en的集合, a m a_m am是常系数。 m e a n ( ) , s t d e v mean(),stdev mean(),stdev表示平均值和标准差。
- 平面度:
同高程一样,平面度阈值更新如下:
f τ , m ← mean ( F m ) + b m ⋅ stdev ( F m ) f_{\tau, m} \leftarrow \operatorname{mean}\left(F_m\right)+b_m \cdot \operatorname{stdev}\left(F_m\right) fτ,m←mean(Fm)+bm⋅stdev(Fm) - 去噪高度
A-GLE 根据估计地平面的高程值的平均值更新 h n o i s e hnoise hnoise:
h noise ← mean ( E 1 ) + δ h_{\text {noise }} \leftarrow \operatorname{mean}\left(E_1\right)+\delta hnoise ←mean(E1)+δ
5时序地面恢复TGR
在实际地面中,平滑度可能会突然变大,由于A-GLE是根据之前的计算结果去更新参数,所以对于
f
n
f_n
fn突然变大的情况需要做出处理。
记
D
m
t
D_{m}^{t}
Dmt为t时刻估计的地面点,将分割不足的bin的
f
n
f_n
fn与
f
τ
,
m
t
f_{\tau,m}^t
fτ,mt比较:
f
τ
,
m
t
=
mean
(
F
m
t
)
+
c
m
⋅
stdev
(
F
m
t
)
f_{\tau, m}^t=\operatorname{mean}\left(F_m^t\right)+c_m \cdot \operatorname{stdev}\left(F_m^t\right)
fτ,mt=mean(Fmt)+cm⋅stdev(Fmt)
c
m
c_m
cm常系数,
F
m
t
F_{m}^t
Fmt是
D
m
t
D_{m}^{t}
Dmt中
f
n
f_n
fn的集合,如果
f
n
<
f
τ
,
m
f_n<f_{\tau,m}
fn<fτ,m 保留地面点,否则去除该bin集合点。
总结
相比于patchwork主要提升的地方有三点:噪点、参数更新、特殊情况处理。两篇论文原文语句读着不是特别顺畅连贯,后面需要进一步分析和阅读代码才能更好理解论文的细节。